A ball of mass m=6kg is shot with speed v=20m/s into a barrel of spring gun of mass M=24kg initially at rest. All surfaces are smooth & spring is massless. Speed of gun after ball stops relative to gun is
2m/s
4m/s
6m/s
8m/s
The correct Answer is:B
To solve the problem, we will use the principle of conservation of momentum. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the System
We have a ball of mass m=6kg moving with a speed v=20m/s and a spring gun of mass M=24kg that is initially at rest. The ball is shot into the gun, and we need to find the speed of the gun after the ball stops relative to it.
Step 2: Apply Conservation of Momentum
According to the law of conservation of momentum, the total momentum before the event must equal the total momentum after the event.
Initial Momentum:
- The initial momentum of the system (ball + gun) is given by the momentum of the ball since the gun is at rest.
Initial Momentum=m⋅v+M⋅0=6⋅20+24⋅0=120kg m/s
Final Momentum:
- After the ball comes to rest relative to the gun, both the ball and the gun move together with a common speed V.
Final Momentum=(m+M)⋅V=(6+24)⋅V=30Vkg m/s
Step 3: Set Initial Momentum Equal to Final Momentum
Now we can set the initial momentum equal to the final momentum:
120=30V
Step 4: Solve for V
To find V, we rearrange the equation:
V=12030=4m/s
Conclusion
The speed of the gun after the ball stops relative to the gun is 4m/s.
---
We have a ball of mass m=6kg moving with a speed v=20m/s and a spring gun of mass M=24kg that is initially at rest. The ball is shot into the gun, and we need to find the speed of the gun after the ball stops relative to it.
According to the law of conservation of momentum, the total momentum before the event must equal the total momentum after the event.
- The initial momentum of the system (ball + gun) is given by the momentum of the ball since the gun is at rest.
Initial Momentum=m⋅v+M⋅0=6⋅20+24⋅0=120kg m/s
- After the ball comes to rest relative to the gun, both the ball and the gun move together with a common speed V.
Final Momentum=(m+M)⋅V=(6+24)⋅V=30Vkg m/s
Now we can set the initial momentum equal to the final momentum:
120=30V
To find V, we rearrange the equation:
V=12030=4m/s
The speed of the gun after the ball stops relative to the gun is 4m/s.
Similar Questions
A ball of mass m is projected with a speed v into the barrel of a spring gun of mass M initially at rest lying on a frictionless surface. The mass sticks in the barrel at the point of maximum compression in the spring. The fraction of kinetic energy of the ball stored in the spring is
View SolutionA bullet of mass 0.1 kg is fired with a speed of 100 m/sec , the mass of gun is 50 kg . The velocity of recoil is
View SolutionA bullet of mass 0.1 kg is fired with a speed of 100 m/sec , the mass of gun is 50 kg . The velocity of recoil is
View SolutionA ball of mass 1kg is thrown up with an initial speed of 4m/s. A second ball of mass 2kg is released from rest from some height as shown in Fig. Choose the correct statement (s).
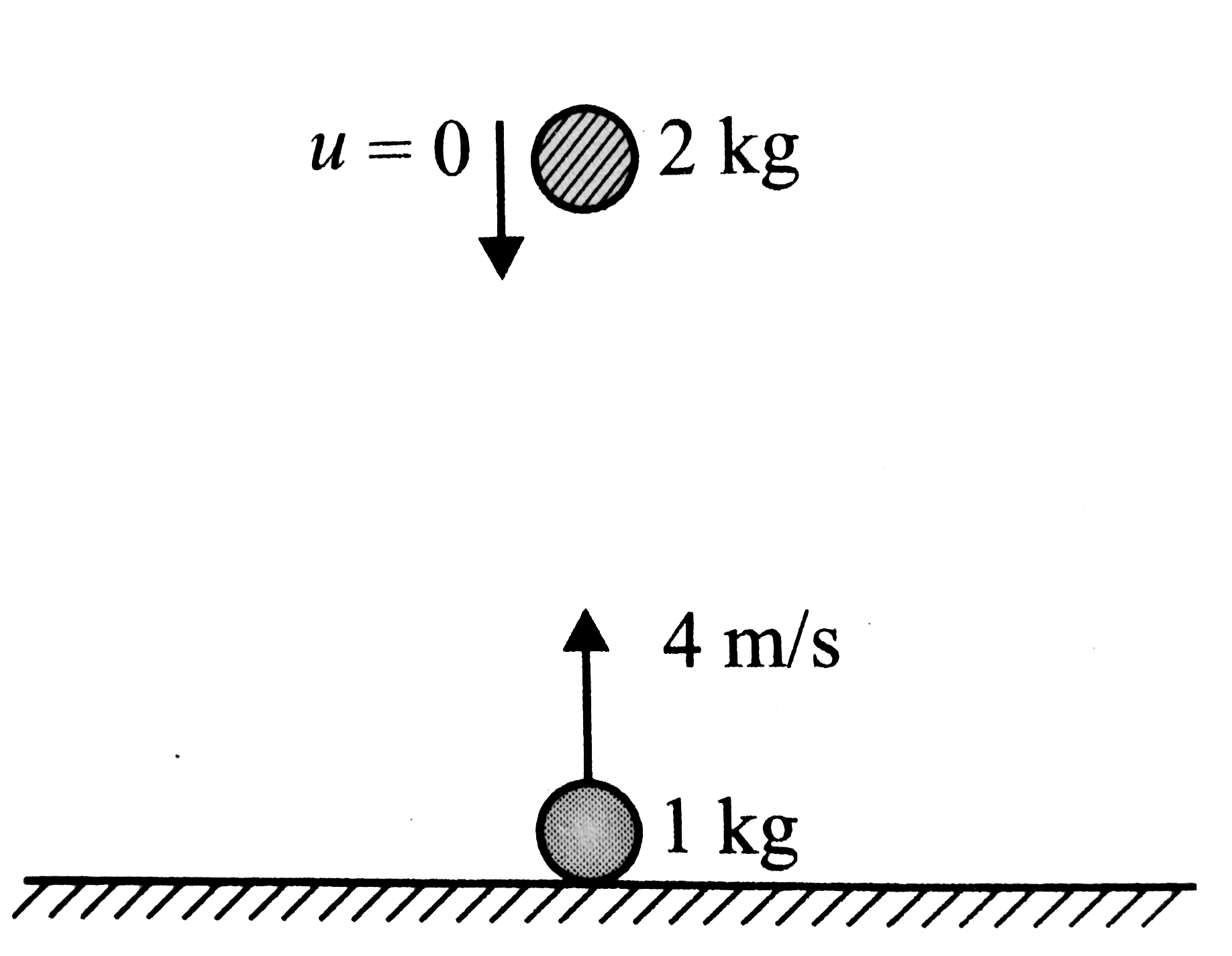 View Solution
View SolutionBall A of mass 1kg moving right with speed 2m/s bounces off ball B of mass 1.5kg, and then moves left with speed 4m/s. Calculate magnitude of impulse (SI Units) received by ball B
 View Solution
View SolutionA bullet of mass m moving at a speed v hits a ball of mass M kept at rest. A small part having mass m ′ breaks from the ball and sticks to the bullet. The remaining ball is found to move at a speed v 1 , in the direction of the bullet. Find the velocity of the bullet after the collision.
View SolutionA loaded spring gun of mass M fires a bullet of mass m with a velocity v at an angle of elevation θ. The gun is initially at rest on a horizontal smooth surface. After firing, the centre of mass of the gun and bullet system
View SolutionA loaded spring gun of mass M fires a bullet of mass m with a velocity v at an angle of elevation θ. The gun is initially at rest on a horizontal smooth surface. After firing, the centre of mass of the gun and bullet system
View SolutionA ball of mass 0.2 kg moves with a velocity of 20m/sec and it stops in 0.1 sec , then the force on the ball is
View SolutionA ball of mass 0.2 kg moves with a velocity of 20m/sec and it stops in 0.1 sec , then the force on the ball is
View Solution

