A light ray incident along vector 2ˆi+4ˆj+√5ˆk strikes in the x−z from medium of refractive index √3 and enters into medium II of refractive index is μ2. The value of μ2 for which the value of angle of refraction becomes 90∘ is
4√35
3√35
2√35
√35
The correct Answer is:B
To solve the problem, we will use Snell's Law, which relates the angles of incidence and refraction to the refractive indices of the two media. The law is given by:
μ1sini=μ2sinr
where:
- μ1 is the refractive index of the first medium,
- μ2 is the refractive index of the second medium,
- i is the angle of incidence,
- r is the angle of refraction.
Step 1: Identify the incident vector and its components
The incident light ray is given by the vector:
→A=2^i+4^j+√5^k
Step 2: Calculate the angle of incidence
The angle of incidence i can be determined using the normal to the interface. Since the light ray strikes the x−z plane, the normal vector is along the y direction, which is ^j.
To find the angle of incidence, we first calculate the magnitude of the incident vector:
|→A|=√(2)2+(4)2+(√5)2=√4+16+5=√25=5
Next, we find the component of the incident vector along the normal direction (which is along ^j):
Ay=4
Using the definition of sine in terms of the angle of incidence:
sini=Ay|→A|=45
Step 3: Set up Snell's Law
Given that the angle of refraction r is 90∘, we know that:
sinr=sin90∘=1
Substituting into Snell's Law:
μ1sini=μ2sinr
Substituting the known values:
√3⋅45=μ2⋅1
Step 4: Solve for μ2
Rearranging the equation gives us:
μ2=√3⋅45
Step 5: Calculate μ2
Now we can compute the value:
μ2=4√35
Final Answer
Thus, the value of μ2 for which the angle of refraction becomes 90∘ is:
μ2=4√35
- μ1 is the refractive index of the first medium,
- μ2 is the refractive index of the second medium,
- i is the angle of incidence,
- r is the angle of refraction.
The incident light ray is given by the vector:
The angle of incidence i can be determined using the normal to the interface. Since the light ray strikes the x−z plane, the normal vector is along the y direction, which is ^j.
Given that the angle of refraction r is 90∘, we know that:
Rearranging the equation gives us:
Now we can compute the value:
Thus, the value of μ2 for which the angle of refraction becomes 90∘ is:
Similar Questions
A lens made of material of Refractive index μ2 is surrounded by a medium of Refractive Index μ1. The focal length f is related as
View SolutionA lens made of material of Refractive index μ2 is surrounded by a medium of Refractive Index μ1. The focal length f is related as
View SolutionA ray of light passes from a medium A having refractive index 1.6 to the medium B having refractive index 1.5. The value of critical angle of medium
A is….
View SolutionIn the figure shown, the angle made by the light ray with the normal in the medium of refractive index √2 is
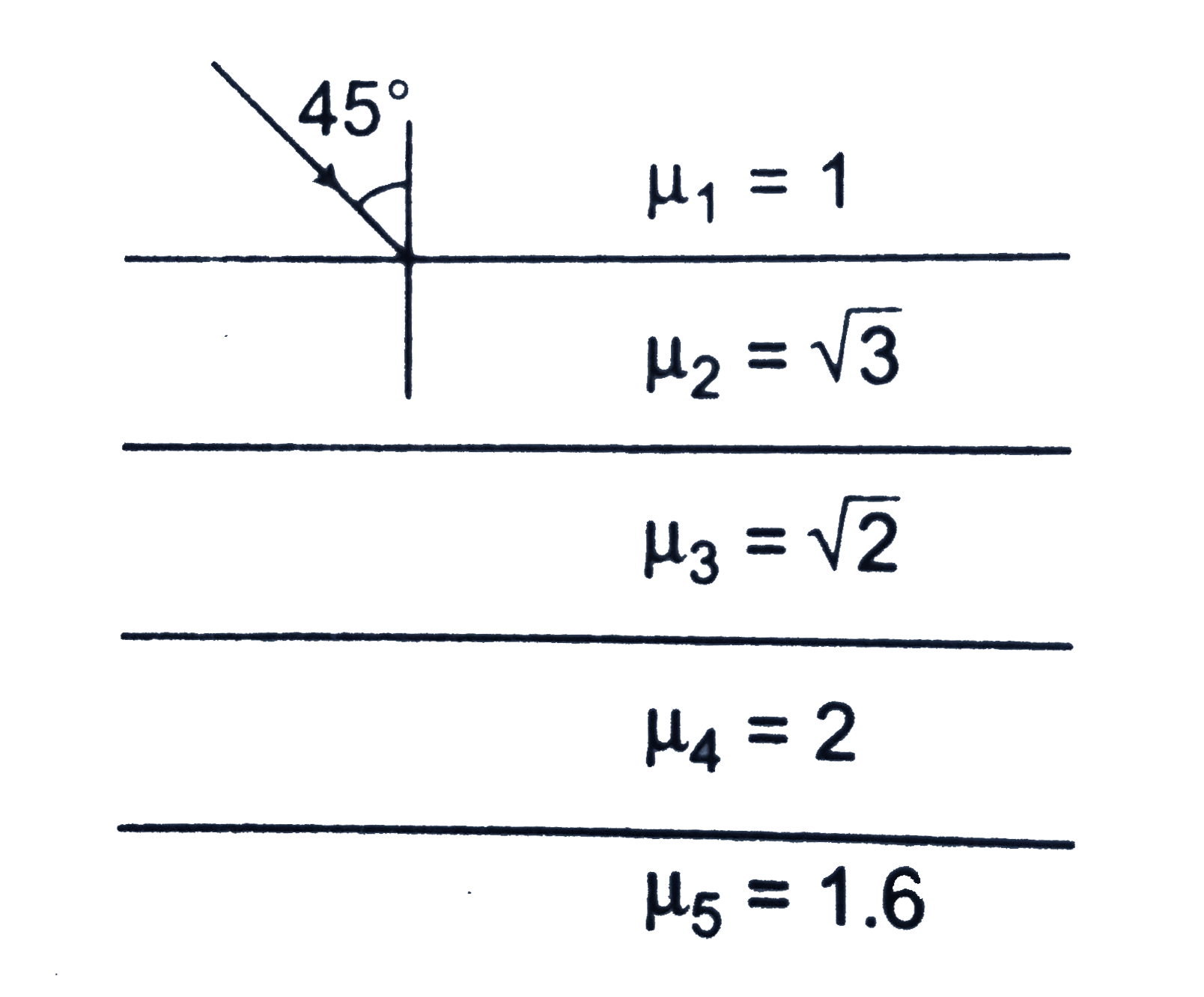
View SolutionA ray of light passes from vaccum into a medium of refractive index n. If the angle of incidence is twice the angle of refraction, then the angle of incidence is
View SolutionA light ray is normally incident onone face of equilateral glass prism of refractive index √2. The deviation of light ray is
View SolutionA prism has refractive index √32 and refractive angle 90∘. Find the minimum deviation produced by prism
View Solutionx-y plane separates two media, z≥0 contains a medium of refractive index 1 and z≤0 contains a medium of refractive index 2. A ray of light is incident from first medium along a vectorˆi+ˆj−ˆk. Find the unit vector along the refracted ray.
View SolutionA ray of light with wavelength 5000 nm travelling from a medium with refractive index (32) suffers partial reflection and refraction in a medium of refractive index (43). Find wavelength of reflected and refracted ray.
View SolutionA ray of light incidents on a refracting surface at 30∘ with the surface . If the angle of refraction is 45∘ refractive index of the medium is
View Solution
