Graphical soluton of a two body head on collision
A block A of mass m moving with a uniform velocity v0 strikes another identical block B kept at rest on a horizontal smooth surface as shown in the figure (i). We can conserve linear momentum.
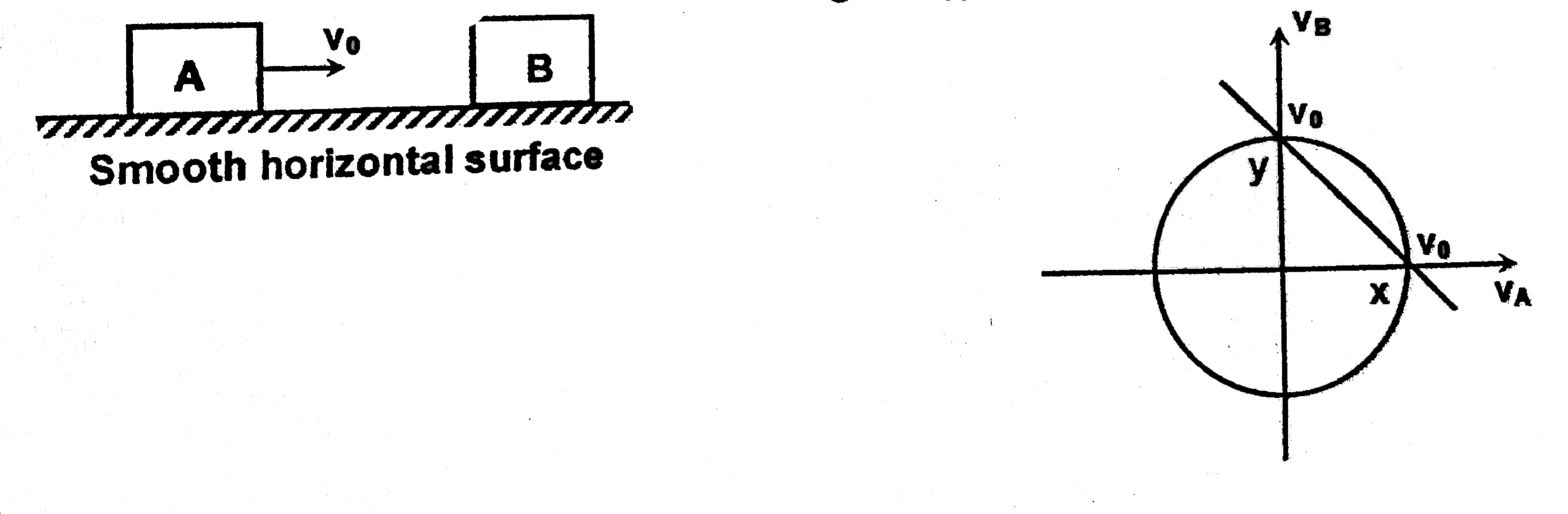
So mv0=mvAmvB (vA and vB are the velocities of the blocks after collision)
∴v0=vA+vB.........(i)
If the collision is perfectly elastic
12mv20=12mv2A+12mv2B
⇒v20=v2A+v2B......(ii)
Both the above equation (i) and (ii) are plotted on vA−vB plane as shown in figure (ii). This plot can be used to find the unknowns vA and vB.
For example the solution of the situation in figure (i) is vA=0,vB=v0 (point y in the plot)
Because vA=v0,vB=0 (point x in the plot) is not physically possible.
In a situation block A is moving with velocity 2m/s an strikes another identical block B kept at rest. The vA−vB plot for the situation is shown. m and l are the intersection points whose vA,vB coordinaes are given in the figure. The coefficient of restitution of the collision is

12
1/3
1
Collision no possible
The correct Answer is:B
e=43−232=13
Similar Questions
Sphere A of mass 'm' moving with a constant velocity u hits another stationary sphere B of the same mass. If e is the co-efficient of restitution, then ratio of velocities of the two spheres vA:vB after collision will be :
View SolutionTwo particles of mass mA and mB and their velocities are VA and VB respectively collides. After collision they interchanges their velocities, then ratio of mAmB is
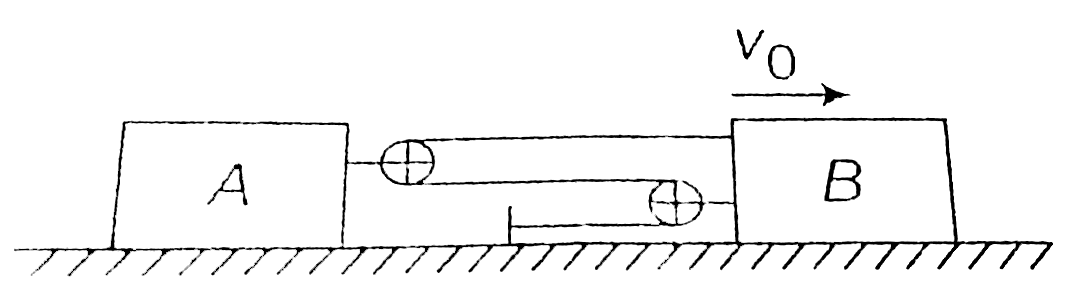
View SolutionBlock B moves to the right with a constant velocity v0. The velocity of body A relative to B is
View SolutionA smooth sledge is moving with constant velocity v0 toward left. A block is pushed toward right with a velocity v0 (relative to ground).

(A) Find the velocity with which the block escapes from the sledge and necessary critical v0 for escaping from the sledge
(B) Will the block launch onto the sledge again?
View SolutionBlock B moves to the right with a constant velocity v_(0) . The velocity of body A relative to B is :
View SolutionTwo particles of mass m_(A) and m_(B) and their velocities are V_(A) and V_(B) respectively collides. After collision they interchanges their velocities, then ratio of m_(A)/m_(B) is
View SolutionSphere A of mass m moving with a constant velocity u hits another stationary sphere B of the same mass. If e is the co-efficient of restitution, then ratio of velocities of the two spheres v_(A):v_(B) after collision will be :
View SolutionBlock B moves to the right with a constant velocity v0. The velocity of body a relative to b is

View Solution
