A conductor of mass m=5kg and length l=4m is placed on horizontal surface and a uniform magnetic field B=2 Tesla exist parallel to horizontal surface but perpendicular to the conductor. Suddenly, a certain amount of charge is passed through it, then it is found to jump to a height h=5m. Then, find the amount of charge that passes through the conductor in coulomb. (take g=10m/s2)
The correct Answer is:00006.25
To solve the problem, we need to find the amount of charge that passes through the conductor when it jumps to a height of 5 meters in a magnetic field. We will use the principles of force, momentum, and energy conservation.
1. Identify the Forces Acting on the Conductor:
The conductor experiences a magnetic force when a current flows through it in the presence of a magnetic field. The force F on the conductor can be expressed as:
F=I⋅L⋅B
where I is the current, L is the length of the conductor, and B is the magnetic field strength.
2. Relate Force to Change in Momentum:
The force also relates to the change in momentum of the conductor. If Δt is the time duration for which the current flows, the change in momentum Δp can be expressed as:
F⋅Δt=m⋅v1
where m is the mass of the conductor and v1 is the final velocity after the force has acted.
3. Use Conservation of Energy:
When the conductor jumps to a height h, its potential energy at the peak is equal to the kinetic energy it had just before jumping:
mgh=12mv21
From this equation, we can solve for v1:
v1=√2gh
4. Substituting v1 into the Momentum Equation:
Substitute v1 back into the momentum equation:
F⋅Δt=m⋅√2gh
5. Substituting the Expression for Force:
Substitute F=I⋅L⋅B into the equation:
I⋅L⋅B⋅Δt=m⋅√2gh
6. Express Current in Terms of Charge:
The current I can be expressed in terms of charge Q and time Δt:
I=QΔt
Substitute this into the equation:
QΔt⋅L⋅B⋅Δt=m⋅√2gh
This simplifies to:
Q⋅L⋅B=m⋅√2gh
7. Solve for Charge Q:
Rearranging gives:
Q=m⋅√2ghL⋅B
8. Substituting Known Values:
Now, substitute the known values:
- m=5kg
- g=10m/s2
- h=5m
- L=4m
- B=2T
Q=5⋅√2⋅10⋅54⋅2
9. Calculating √2gh:
√2gh=√2⋅10⋅5=√100=10
10. Final Calculation:
Substitute back into the equation for Q:
Q=5⋅108=508=254C
Final Answer:
The amount of charge that passes through the conductor is 254C.
The conductor experiences a magnetic force when a current flows through it in the presence of a magnetic field. The force F on the conductor can be expressed as:
F=I⋅L⋅B
where I is the current, L is the length of the conductor, and B is the magnetic field strength.
The force also relates to the change in momentum of the conductor. If Δt is the time duration for which the current flows, the change in momentum Δp can be expressed as:
F⋅Δt=m⋅v1
where m is the mass of the conductor and v1 is the final velocity after the force has acted.
When the conductor jumps to a height h, its potential energy at the peak is equal to the kinetic energy it had just before jumping:
mgh=12mv21
From this equation, we can solve for v1:
v1=√2gh
Substitute v1 back into the momentum equation:
F⋅Δt=m⋅√2gh
Substitute F=I⋅L⋅B into the equation:
I⋅L⋅B⋅Δt=m⋅√2gh
The current I can be expressed in terms of charge Q and time Δt:
I=QΔt
Substitute this into the equation:
QΔt⋅L⋅B⋅Δt=m⋅√2gh
This simplifies to:
Q⋅L⋅B=m⋅√2gh
Rearranging gives:
Q=m⋅√2ghL⋅B
Now, substitute the known values:
- m=5kg
- g=10m/s2
- h=5m
- L=4m
- B=2T
√2gh=√2⋅10⋅5=√100=10
Substitute back into the equation for Q:
Q=5⋅108=508=254C
The amount of charge that passes through the conductor is 254C.
Similar Questions
A conductor of length l is placed perpendicular to a horizontal uniform magnetic field B.Suddenly, a certain amount of charge is passed throgh it, when it is found to jump to a height h. The amount of charge that passes through the conductor is
View SolutionA conducting rod of mass m and length l is placed over a smooth horizontal surface. A uniform magnetic field B is acting perpendicular to the rod. Charge q is suddenly passed through the rod and it acquires an initial velocity v on the surface, then q is equal to
View SolutionA current of 1.5A flows through a conductor for 2.0s. What amount of charge passes through the conductor ?
View SolutionA conductor of length 0.1m is moving with a velocity of 4m/s in a uniform magnetic field of 2T as shown in the figure. Find the emf induced ?
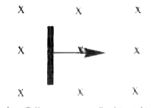
View SolutionA ball of mass 1 kg is dropped from 20 m height on ground and it rebounds to height 5m. Find magnitude of change in momentum during its collision with the ground. (Take g=10m/s2)
View SolutionA conducting ring of mass 2kg, radius 0.5m carries a current of 4A. It is placed on a smooth horizontal surface. When a horizontal magnetic field of 10 T parallel to the diameter of the ring is applied, the initial acceleration is (in rad/sec2)

View SolutionA conductor of length 0.1m is moving with a velocity of 4m/ s in a uniform magnetic field of 2T as shown in the figure. Find the emf induced ?
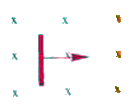
View SolutionA block of mass 10 kg, moving with acceleration 2m/s2 on horizontal rough surface is shown in figure
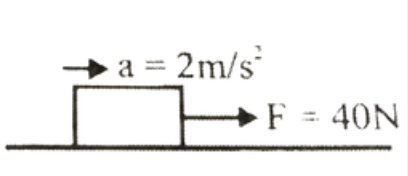
View SolutionA loop of area 1m2 is placed in a magnetic field B=2T, such that plane of the loop is parallel to the magnetic field. If the loop is rotated by 180∘, the amount of net charge passing through any point of loop, it its resistance is 10Ω is
View SolutionA charged particle of charge 1 mC and mass 2g is moving with a speed of 5m/s in a uniform magnetic field of 0.5 tesla. Find the maximum acceleration of the charged particle
View Solution
