If voltage applied to X -ray tube increased fromV=10kV to 20kV. The wave length interval between Kα−line and short wave cut off continuous X-ray increases by factor of 3Rhce=13.6V where R is Rydberg constant h is plank's constant c is speed of light in vacuum and e is charge on electron
Atomic no. of tangent metal used is 29
Cut- off wavelength when V=10kV is 1.2Å
Cut off wavelength when V=10kV is 2Å
Atomic no. of target metal used is26
The correct Answer is:A
To solve the problem, we need to analyze the relationship between the voltage applied to the X-ray tube and the wavelengths of the emitted X-rays, specifically the Kα line and the short wave cut-off continuous X-ray.
1. Understand the relationship between voltage and wavelength:
The energy of the emitted X-rays is related to the voltage (V) applied to the X-ray tube. The cut-off wavelength (λ) is given by the formula:
λ=hceV
where h is Planck's constant, c is the speed of light, and e is the charge of an electron.
2. Calculate the cut-off wavelengths for the two voltages:
For V1=10kV=10,000V:
λ1=hceV1
For V2=20kV=20,000V:
λ2=hceV2
3. Set up the equation for the wavelength interval:
The problem states that the wavelength interval between the Kα line and the short wave cut-off continuous X-ray increases by a factor of 3:
λ2−λ1=3⋅λ1
Rearranging gives:
λ2=4λ1
4. Substituting the values of λ:
Substitute the expressions for λ1 and λ2:
hceV2=4⋅hceV1
5. Canceling common terms:
Since hc/e is common in both terms, we can cancel it out:
1V2=4⋅1V1
6. Substituting the voltage values:
Substitute V1=10,000V and V2=20,000V:
120,000=4⋅110,000
This confirms the relationship holds true.
7. Finding the atomic number (Z):
The relationship between the wavelength and atomic number for the Kα line can be expressed as:
1λ=R⋅(Z−1)2
where R is the Rydberg constant. We can relate this to our previous equations to find Z.
8. Using the derived relationship:
From the previous steps, we can derive:
Z=√1λ⋅1R+1
Substitute the known values to find Z.
9. Final calculations:
After substituting the values and solving, we find that Z=29.
10. Finding λ1:
Using the formula for λ1:
λ1=hceV1
Substitute the known constants and V1 to find λ1.
The energy of the emitted X-rays is related to the voltage (V) applied to the X-ray tube. The cut-off wavelength (λ) is given by the formula:
λ=hceV
where h is Planck's constant, c is the speed of light, and e is the charge of an electron.
For V1=10kV=10,000V:
λ1=hceV1
For V2=20kV=20,000V:
λ2=hceV2
The problem states that the wavelength interval between the Kα line and the short wave cut-off continuous X-ray increases by a factor of 3:
λ2−λ1=3⋅λ1
Rearranging gives:
λ2=4λ1
Substitute the expressions for λ1 and λ2:
hceV2=4⋅hceV1
Since hc/e is common in both terms, we can cancel it out:
1V2=4⋅1V1
Substitute V1=10,000V and V2=20,000V:
120,000=4⋅110,000
This confirms the relationship holds true.
The relationship between the wavelength and atomic number for the Kα line can be expressed as:
1λ=R⋅(Z−1)2
where R is the Rydberg constant. We can relate this to our previous equations to find Z.
From the previous steps, we can derive:
Z=√1λ⋅1R+1
Substitute the known values to find Z.
After substituting the values and solving, we find that Z=29.
Using the formula for λ1:
λ1=hceV1
Substitute the known constants and V1 to find λ1.
Similar Questions
when the voltage applied to an X-ray tube increases from V1=10kV to V2=20kV, the wavelenght interval between Kα line and cut-off wavelenght of continuous spectrum increases by a factor of 3. Atomic number of the metallic target is
View SolutionWhen the voltage applied to an X-ray tube increased from V1=15.5kV to V2=31kV the wavelength interval between the Kα line and the cut-off wavelength of te continuous X-ray spectrum increases by a factor of 1.3. If te atomic number of the element of the target is z. Then the value of z13 will be: (take hc=1240eVnm and R=1×107m)
View SolutionThe wavelength interval between kα line and λmin of continuous X-ray spectrum of metal becomes 2 times when operating voltage is charged from 10 kV to x kV. Find x. What will happen to wavelength interval between kα line and kβ line in this case ? (Z=28)
View SolutionThe constant 'a' Mosely's law √v=a(Z−b) for kαX−rays is related to Rydberg constant R as ('c' is the speed of light)
View SolutionThe electron in a Li++ ion is the nth shell , n being very large. One of the K-electron in another matallic atom has been knocked out. The second matel has four orbits. Now, we take two sample one of Li++ ion and the other of the second mateillic ions. Suppose the probability of electronic transition from higher to lower energy level is directly proportional to the energy difference between the two shells. Take hc=1224eVnm , where h is Planck's constant and c the velocity of light in vacuum. It is found that major electromagnetic wavws emitted from the two sample are identical. Now , answer the following questions:
The wavelength of this major X-ray isView SolutionThe electron in a Li++ ion is the nth shell , n being very large. One of the K-electron in another matallic atom has been knocked out. The second matel has four orbits. Now, we take two sample one of Li++ ion and the other of the second mateillic ions. Suppose the probability of electronic transition from higher to lower energy level is directly proportional to the energy difference between the two shells. Take hc=1224eVnm , where h is Planck's constant and c the velocity of light in vacuum. It is found that major electromagnetic wavws emitted from the two sample are identical. Now , answer the following questions:
What is the major X-ray emitted by the sample?View SolutionThe electron in a Li++ ion is the nth shell , n being very large. One of the K-electron in another matallic atom has been knocked out. The second matel has four orbits. Now, we take two sample one of Li++ ion and the other of the second mateillic ions. Suppose the probability of electronic transition from higher to lower energy level is directly proportional to the energy difference between the two shells. Take hc=1224eVnm , where h is Planck's constant and c the velocity of light in vacuum. It is found that major electromagnetic wavws emitted from the two sample are identical. Now , answer the following questions:
What is the X-ray having least intensity emitted by the second sample?View SolutionIn the Coolidge tube experiment, if the applied voltage is increased to three times, the short wavelength limit of continuous X- ray spectrum shift by 20 pm. What is the initial voltage (in kV) applied to the tube?
View SolutionHydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., mvr=(nh/2π), where m= mass of the electron , v=velocity of the electron in the orbit , r=radius of the orbit , and n=1,2,3.... When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is λ.
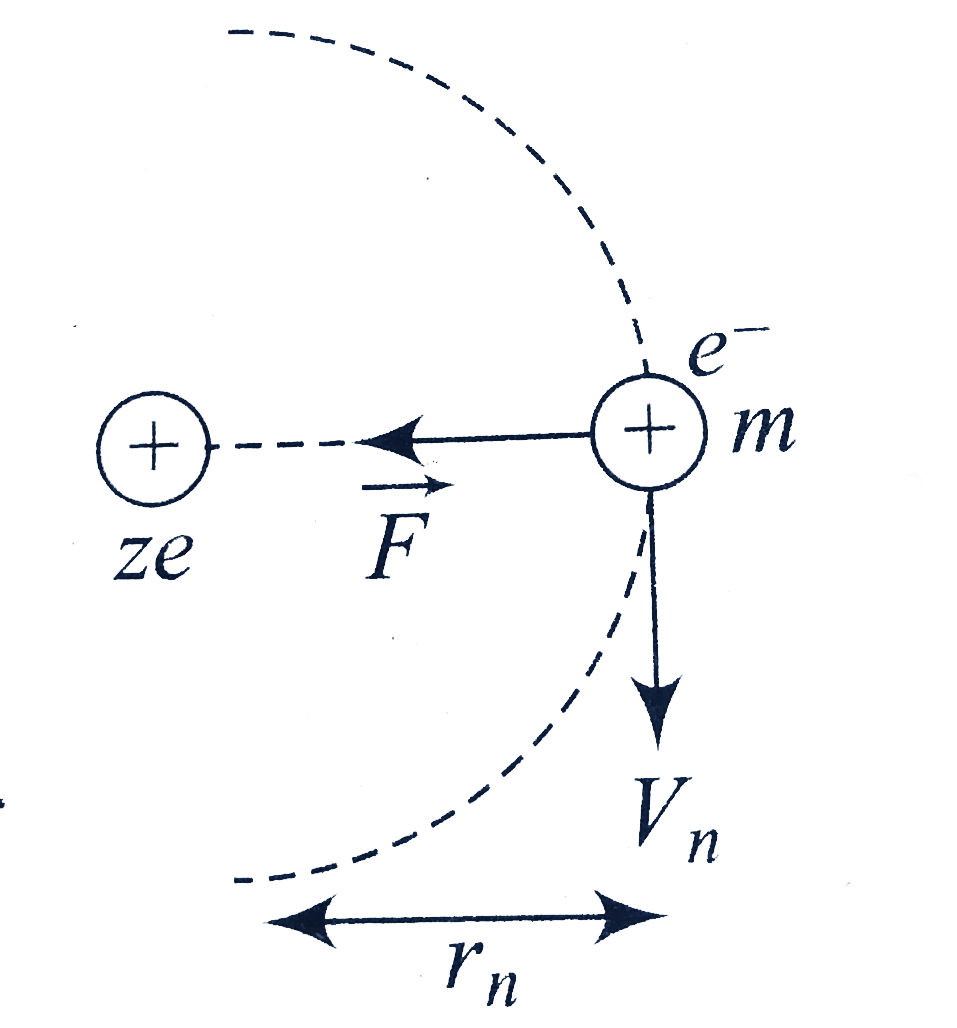
we find that 1λ=R[1J2−1K2], where R is
Rydberg's constant.
On a different planet, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was P=2n(h/2π). i.e., an even multiple of (h/2π).
Answer the following questions regarding the other planet based on above passage:
In our world, the ionization potential energy of a hydrogen atom is 13.6eV. On the other planet, this ionization potential energy will beView SolutionHydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., mvr=(nh/2π), where m= mass of the electron , v=velocity of the electron in the orbit , r=radius of the orbit , and n=1,2,3.... When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is λ.
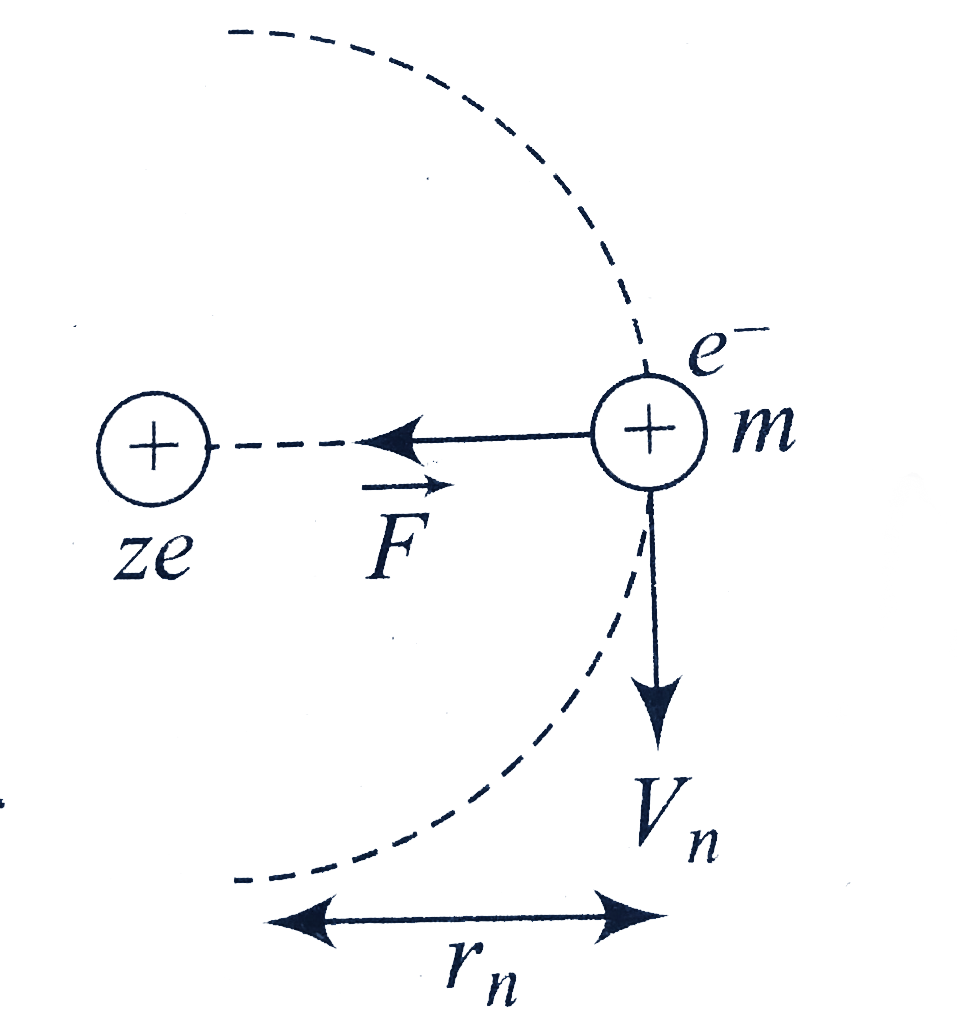
we find that 1λ=R[1J2−1K2], where R is
Rydberg's constant.
On a different planed, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was P=2n(h/2π). i.e., an even multipal of (h/2π).
Answer the following questions regarding the other planet based on above passage:
In our world, the velocity of electron is v0 when the hydrogen atom is in the ground state on the other planet should beView Solution

