One mole of component P and two moles of component Q are mixed at 27∘C to form an ideal binary solution. Select the correct option for given information?
a) ΔSmix=3.82calk−1
b) ΔHmix=0
c) ΔSmix=0
d) ΔGmix=−1145.7 cal
The correct Answer is:A, B, D
To solve the problem of mixing one mole of component P and two moles of component Q at 27°C to form an ideal binary solution, we will follow these steps:
Step 1: Identify the components and their moles
- Let component P be the solute with NP=1 mole.
- Let component Q be the solvent with NQ=2 moles.
Step 2: Calculate the total number of moles
Total moles Ntotal=NP+NQ=1+2=3 moles.
Step 3: Calculate the mole fractions
- Mole fraction of P (XP):
XP=NPNtotal=13
- Mole fraction of Q (XQ):
XQ=NQNtotal=23
Step 4: Use the Gibbs free energy of mixing formula
For an ideal binary solution, the Gibbs free energy of mixing (ΔGmix) is given by:
ΔGmix=RT(NPlnXP+NQlnXQ)
Where:
- R is the universal gas constant (approximately 2cal/K⋅mol),
- T is the temperature in Kelvin (27°C = 300 K).
Step 5: Substitute the values into the Gibbs free energy equation
ΔGmix=2cal/K⋅mol×300K(1ln(13)+2ln(23))
Step 6: Calculate the logarithmic values
- ln(13)≈−1.0986
- ln(23)≈−0.4055
Step 7: Plug in the logarithmic values
ΔGmix=2×300(1×(−1.0986)+2×(−0.4055))
=600(−1.0986−0.8110)
=600×(−1.9096)≈−1145.76calories
Step 8: Determine the change in enthalpy and entropy
For an ideal solution:
- ΔHmix=0 (no heat absorbed or released during mixing).
- Use the relation:
ΔGmix=ΔHmix−TΔSmix
Since ΔHmix=0:
ΔGmix=−TΔSmix⟹ΔSmix=−ΔGmixT
Substituting the values:
ΔSmix=−−1145.76300≈3.82cal/K
Conclusion
The results are:
- ΔGmix≈−1145.76calories
- ΔHmix=0
- ΔSmix≈3.82cal/K
Correct Options
Based on the calculations:
- Option A: ΔSmix=3.82cal/K (Correct)
- Option B: ΔHmix=0 (Correct)
- Option D: ΔGmix=−1145.7calories (Correct)
- Let component P be the solute with NP=1 mole.
- Let component Q be the solvent with NQ=2 moles.
Total moles Ntotal=NP+NQ=1+2=3 moles.
- Mole fraction of P (XP):
XP=NPNtotal=13
- Mole fraction of Q (XQ):
XQ=NQNtotal=23
For an ideal binary solution, the Gibbs free energy of mixing (ΔGmix) is given by:
ΔGmix=RT(NPlnXP+NQlnXQ)
Where:
- R is the universal gas constant (approximately 2cal/K⋅mol),
- T is the temperature in Kelvin (27°C = 300 K).
ΔGmix=2cal/K⋅mol×300K(1ln(13)+2ln(23))
- ln(13)≈−1.0986
- ln(23)≈−0.4055
ΔGmix=2×300(1×(−1.0986)+2×(−0.4055))
=600(−1.0986−0.8110)
=600×(−1.9096)≈−1145.76calories
For an ideal solution:
- ΔHmix=0 (no heat absorbed or released during mixing).
- Use the relation:
ΔGmix=ΔHmix−TΔSmix
Since ΔHmix=0:
ΔGmix=−TΔSmix⟹ΔSmix=−ΔGmixT
Substituting the values:
ΔSmix=−−1145.76300≈3.82cal/K
The results are:
- ΔGmix≈−1145.76calories
- ΔHmix=0
- ΔSmix≈3.82cal/K
Based on the calculations:
- Option A: ΔSmix=3.82cal/K (Correct)
- Option B: ΔHmix=0 (Correct)
- Option D: ΔGmix=−1145.7calories (Correct)
Similar Questions
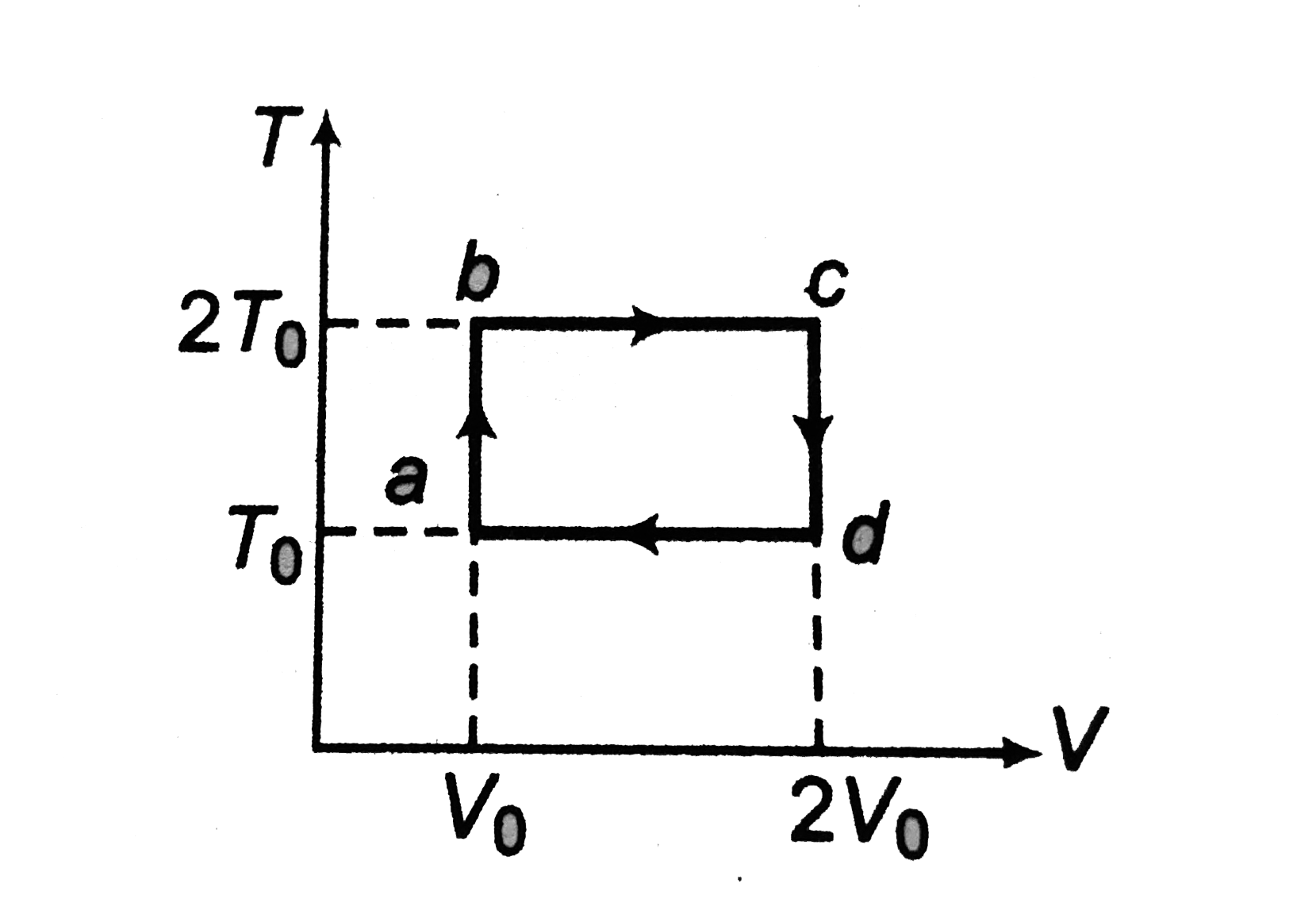
T-V diagram of two moles of a monoatomic gas is as shown in figure.
For the process abcda choose the correct options given below
 View Solution
View SolutionPAandPB are the vapour pressure of pure liquid components ,Aand B respectively of an ideal binary solution,If xA represents the mole fraction of component A, the total pressure of the solution will be
View Solution
Knowledge Check
- Question 1 - Select One
The given pie diagram represents different components of the soil. Identify P,Q and R and select the correct option
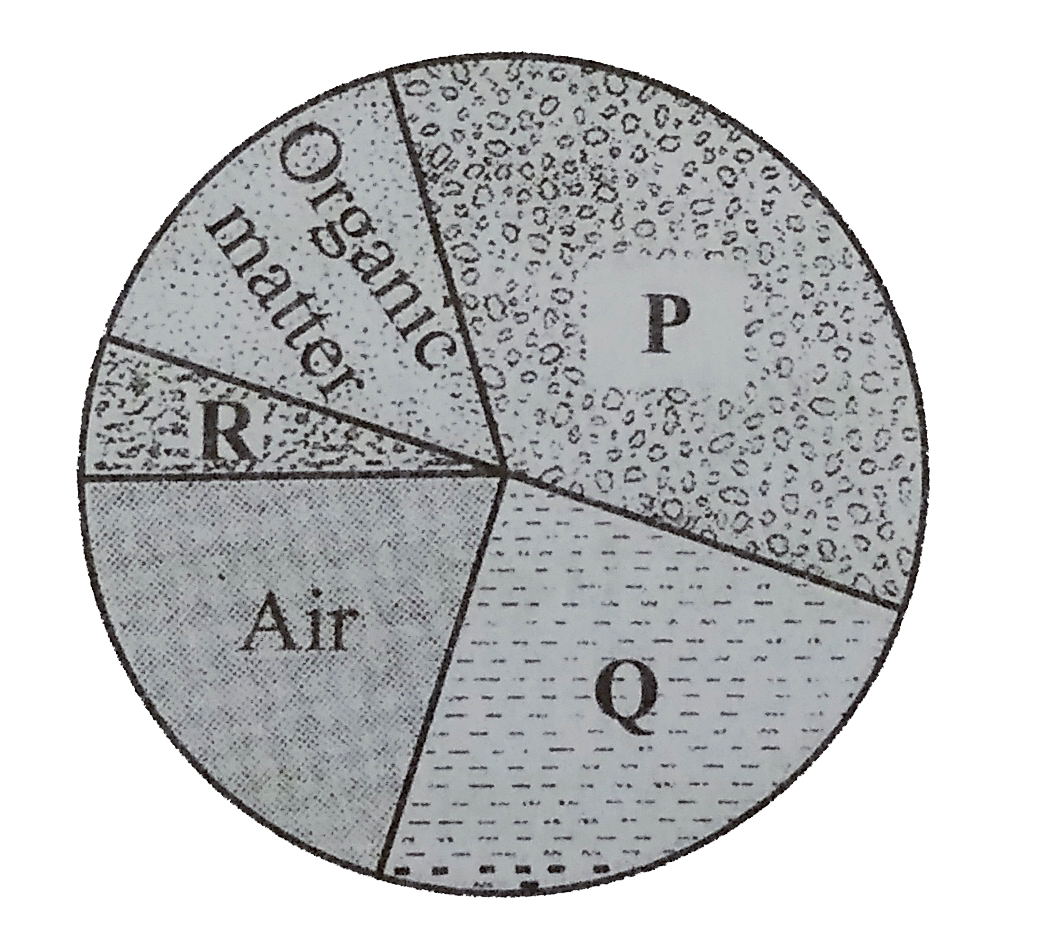 APQRWaterBiotaMineral saltsBPQRMineral saltsBiotaWaterCPQRMineral saltsWaterBiotaDPQRBiotaWaterMineral water
APQRWaterBiotaMineral saltsBPQRMineral saltsBiotaWaterCPQRMineral saltsWaterBiotaDPQRBiotaWaterMineral water - Question 2 - Select One
3 moles of P and 2 moles of Q are mixed , what will be their total vapour pressure in the solution if their partial vapour pressures are 80 and 60 torr respectively ?
A80 torrB140 torrC72 torrD70 torr
Four moles of hydrogen , two moles of helium and one mole of water vapour form an ideal gas mixture. What is the molar specific heat at constant pressure of mixture?
View SolutionOne mole of an ideal monoatomic gas is taken through a cyclic process as shown. Choose the correct option(s).
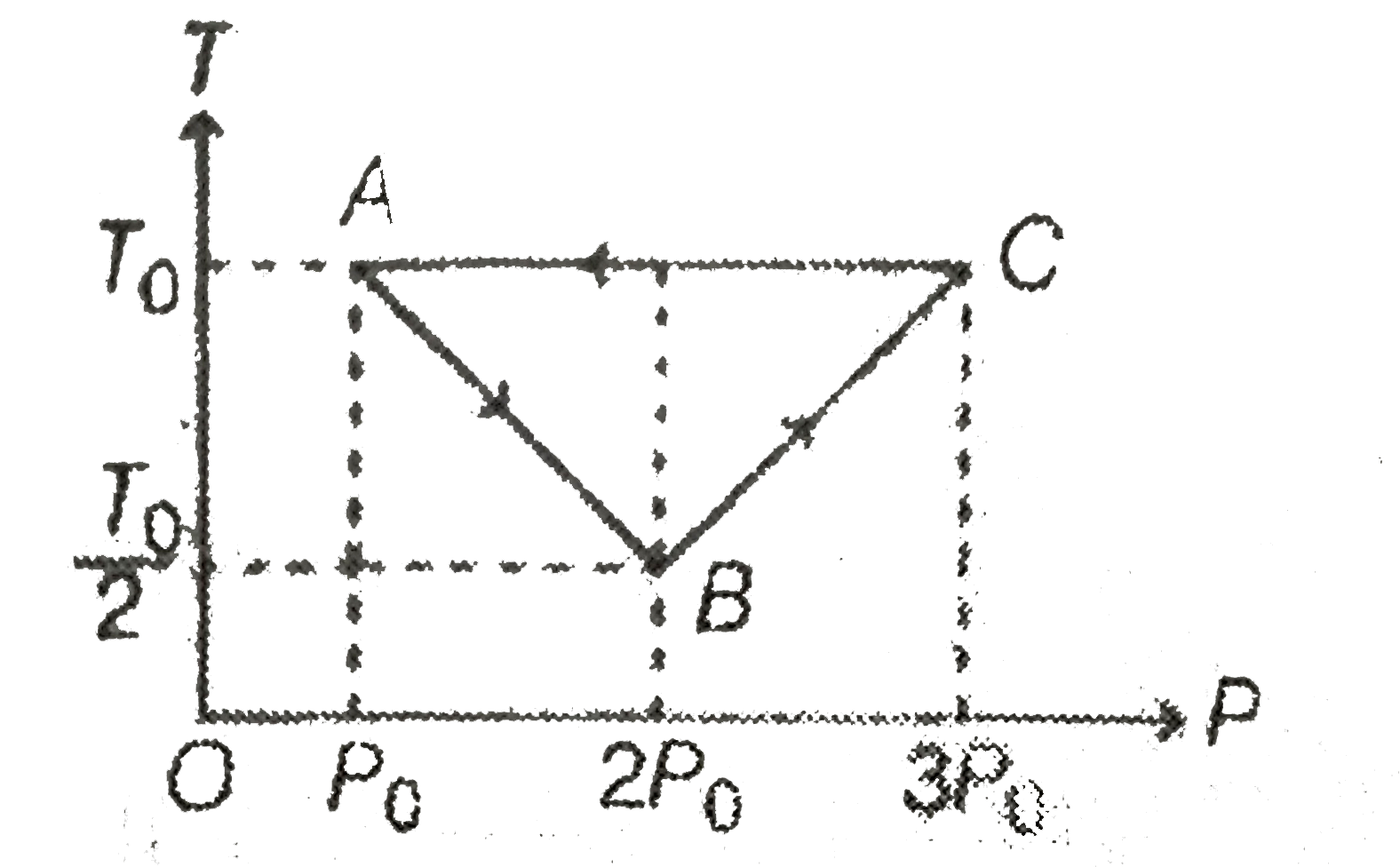 View Solution
View SolutionWhich of the following is true when components forming an ideal solution are mixed?
View SolutionA solution of two components containing n1 moles of 1st component and n2 moles of the 2nd component is prepared . M1 and M2 are the molecular weights of component 1 and 2 respectively . If d is the density of the solution in gmL−1 , C2 is the molarity and x2 is the mole fraction of the 2nd component , then C2 can be expressed as :
View Solution1 mole heptane (V.P=92mmofHg) is mixed with 4 mol. Octane (V.P=31 mm of Hg), form an ideal solution. Find out the vapour pressure of solution.
View Solution1 mole heptane (V.P=92mmofHg) is mixed with 4 mol. Octane (V.P=31 mm of Hg), form an ideal solution. Find out the vapour pressure of solution.
View Solution

