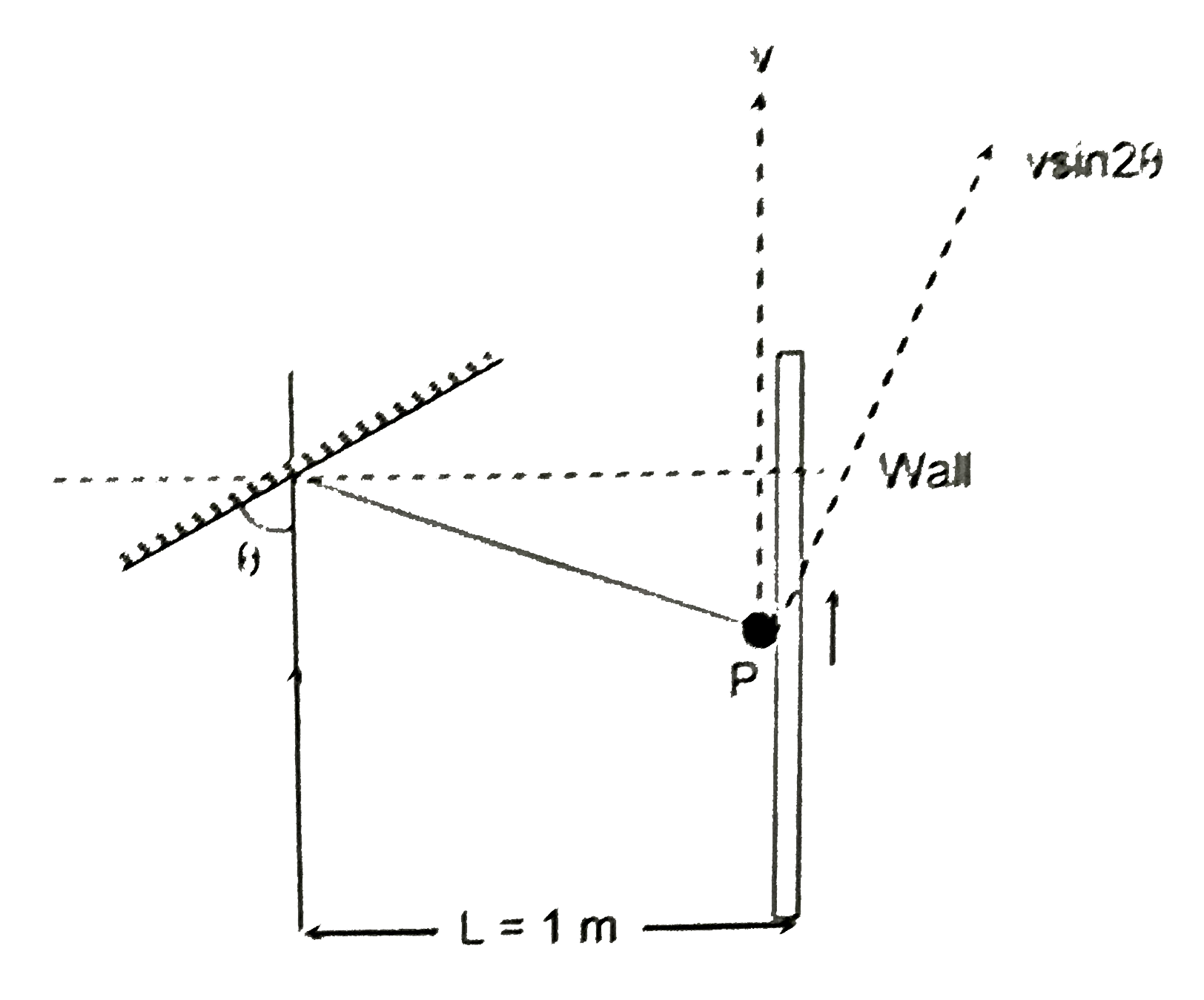
A light ray is incident on a rotating mirror, which is rotating with angular speed $3 r a d / s$ as shown in figure. The speed of bright spot on the wall when $θ = 30^{\circ}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:8

$tan (2 θ - 90) = \frac{Y}{L}$
$y = - L cot 2 θ$
$\frac{d y}{d t} = - L \times (- cos e c^{2} 2 θ) \times 2 \frac{d θ}{d t}$
$= 2 L (cos e c^{2} 2 θ) \frac{d θ}{d t}$

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Similar Questions

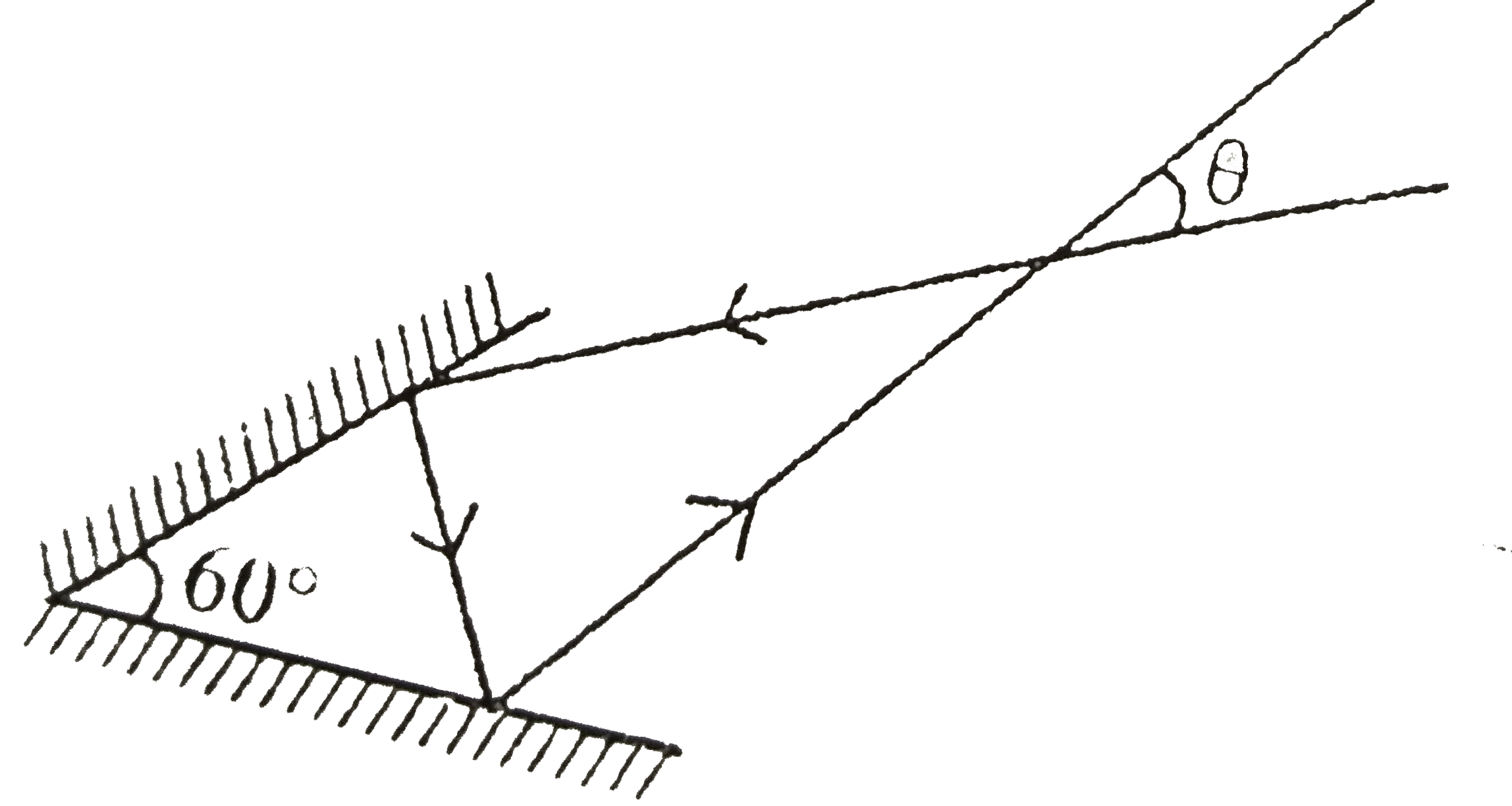
A light ray is incident on a plane mirror, which after getting reflected strikers another plane mirror, as shwon in figure. The angle between the two mirrors is $60^{\circ}$ . Find the angle $' θ'$ shown in figure.

View Solution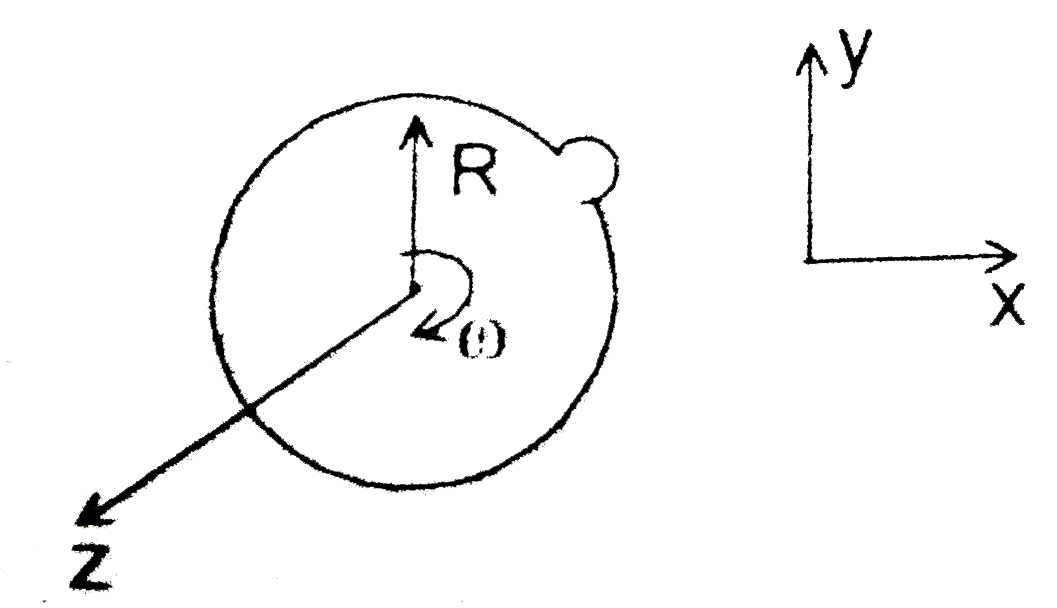
A small pulse is generated on a ring rotating with constant angular velocity $ω$ as shown in the figure. Then the speed of pulse with respect to ground.
View Solution
A uniform rod of length $l$ is rotating with constant angular speed $ω$ as shown in figure. Choose the graph which correctly shows the variation of $T$ with $x$ .

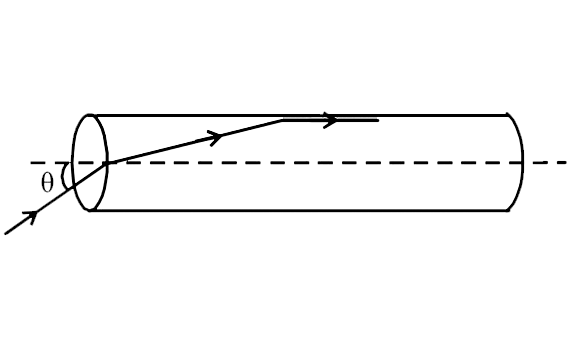
View Solution
A transparent solid cylindrical rod has a refractive index of $\frac{2}{\sqrt{3}}$ .It is surrounded by air. A light ray is incident at the mid-point of one end of the rod as shown in the figure. The incident angle $θ$ for which the light ray grazes along the wall of the rod is:

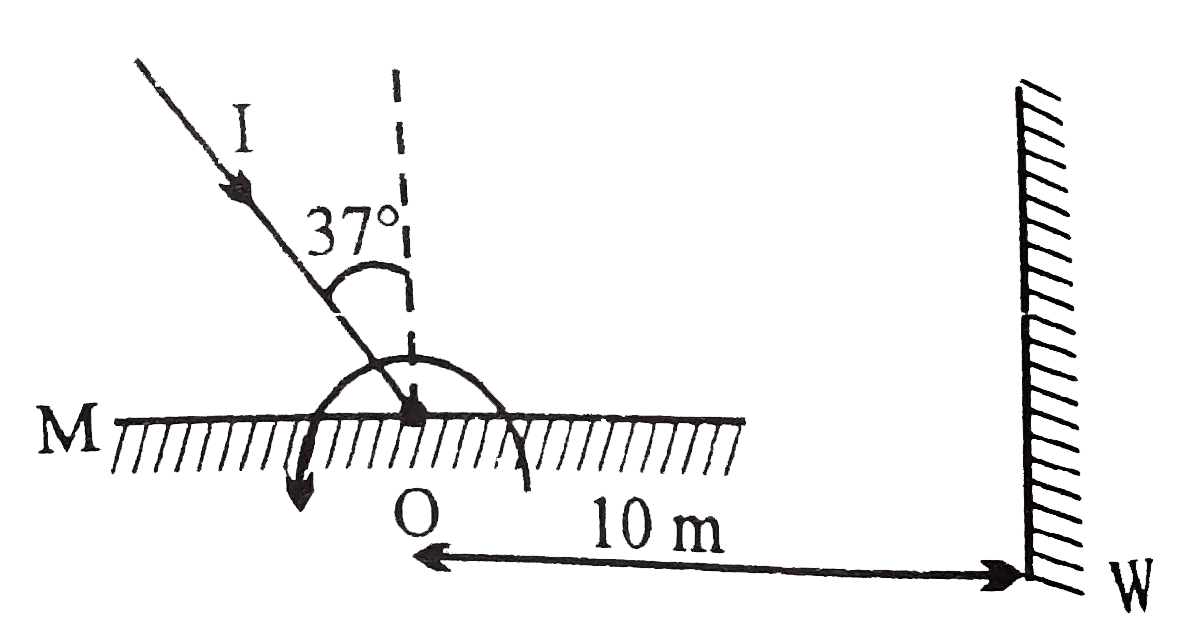
View Solution
A light ray $I$ is incident on a plane mirror $M$ .The mirror is rotated in the direction as shown in the figure by an arrow at frequency $\frac{9}{π} rev / sec$ ,The light reflected by the mirror is received on the wall $W$ at a distance $10 m$ from the axis of rotation .When the angle of incidence becomes $37^{\circ}$ find the speed of the spot (a point) on the wall?

View Solution
A solid sphere of radius $2.45 m$ is rotating with an angular speed of $10 r a d / s$ . When this rotating sphere is placed on a rough horizontal surface then after sometime it starts pure rolling. Find the linear speed of the sphere after it starts pure rolling.
View Solution
A disc of radius 10 cm is rotating about its axis at an angular speed of 20 rad/s. Find the linear speed of
a. a point on the rim,
b. the middle point of the radius.
View Solution
Using the concept of instantaneous axis of rotation. Find speed of particle P as shown in figure, under pure rolling condition.
View Solution
A liquid of density $' ρ'$ is rotated with an angular speed $' ω'$ as shown in figure. Using the pressure equation concept find the equation of free surface of the liquid.
.
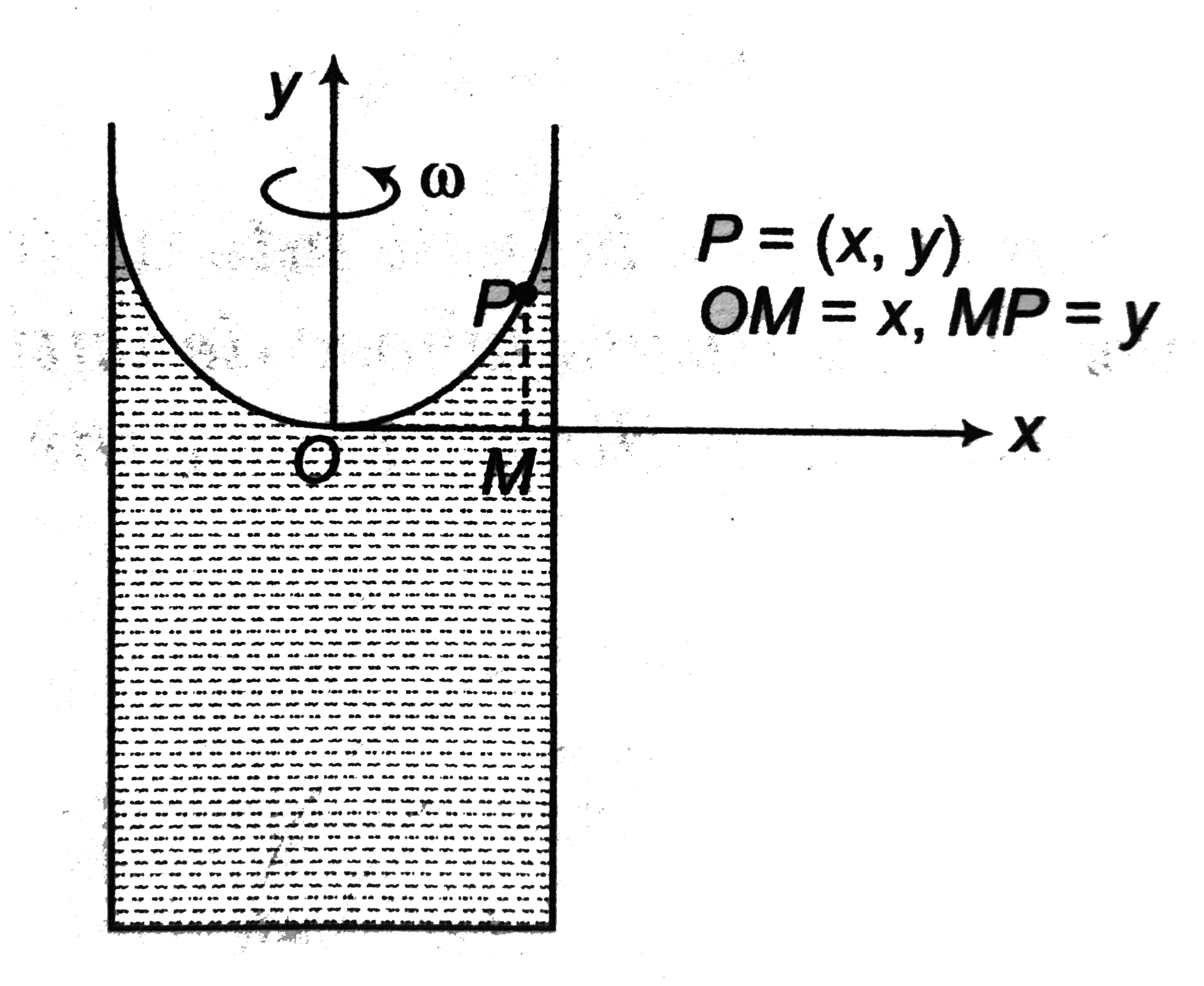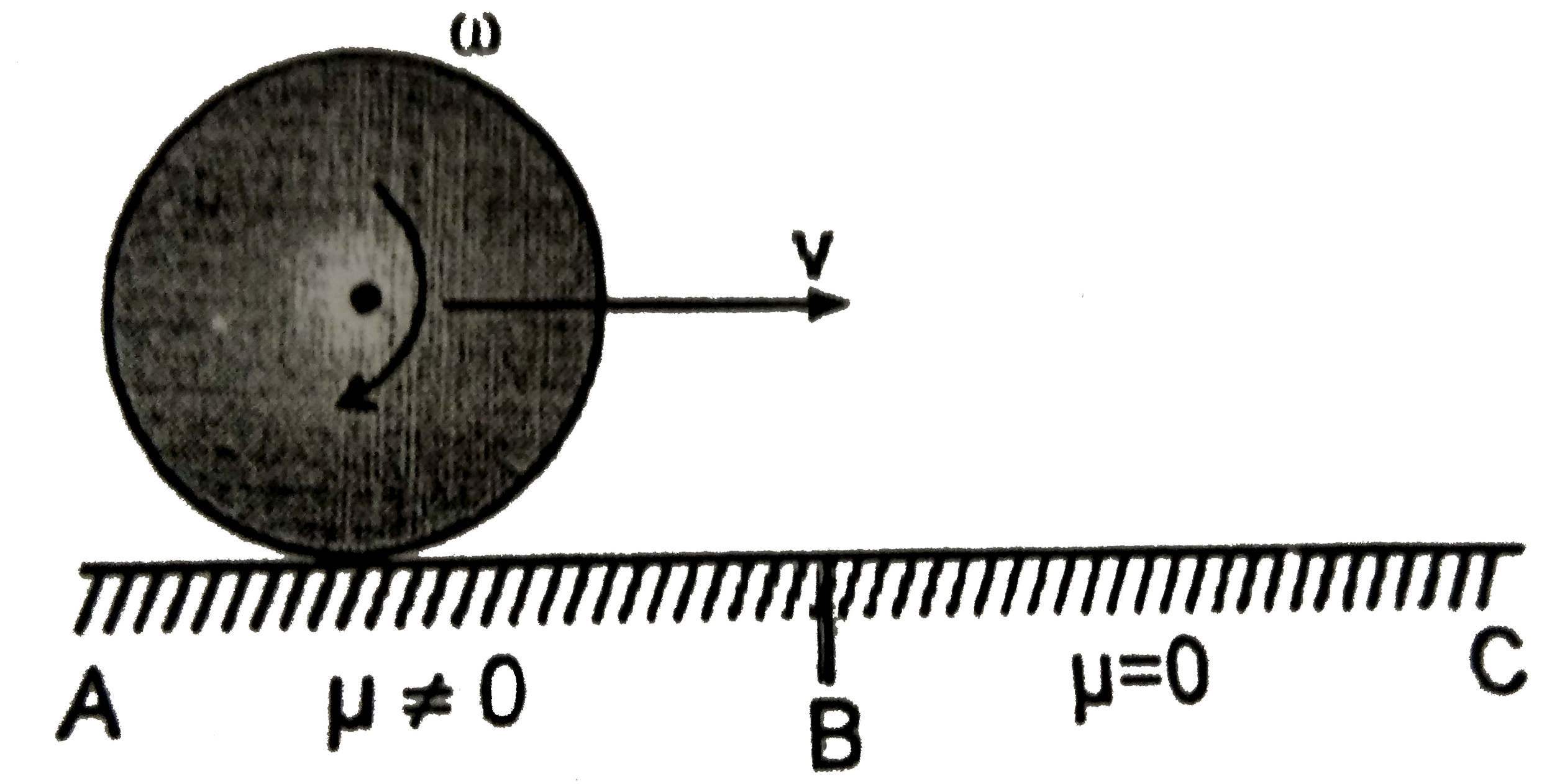
View Solution
As shown in the figure, a disc of mass $m$ is rolling without slipping a angular velocity $ω$ . When it crosses point $B$ disc will be in $:$

View Solution

Recommended Questions

Home
Ask Doubt
Profile