A capillary tube is made of glass of refractive index n'. The outer radius of the tube is R. The tube is filled with a liquid of refractive index n<n'. What should be the minimum internal radius of the tube so that any ray that hits the tube would enter the liquid.
Rn
Rn'
Rn'n
Rnn'
To solve the problem of determining the minimum internal radius of a capillary tube filled with a liquid of refractive index n (where n<n′, the refractive index of the glass), we need to ensure that any ray of light that hits the tube will enter the liquid. Here’s a step-by-step solution:
Step 1: Understand the Geometry and Refraction
We have a capillary tube made of glass with an outer radius R and filled with a liquid of refractive index n. We need to determine the minimum internal radius r of the tube such that any ray of light that strikes the tube will not enter the liquid.
Step 2: Consider the Limiting Case
The critical scenario occurs when the incident ray hits the outer surface of the tube at the steepest angle possible, which is 90∘. In this case, the ray will refract into the glass.
Step 3: Apply Snell's Law at the First Boundary
Using Snell's Law at the air-glass boundary:
n1sini=n2sinr
Here, n1=1 (for air), i=90∘, and n2=n′ (for glass). Thus:
1⋅sin(90∘)=n′⋅sin(ϕ)
This simplifies to:
sin(ϕ)=1n′
Let’s label this as Equation (1).
Step 4: Apply Snell's Law at the Second Boundary
Now, we need to consider the boundary between the glass and the liquid. For total internal reflection to occur at this boundary, the angle of refraction r must be 90∘. Thus, applying Snell's Law again:
n′sin(θ)=nsin(90∘)
This simplifies to:
n′sin(θ)=n
From this, we can express sin(θ):
sin(θ)=nn′
Let’s label this as Equation (2).
Step 5: Relate the Angles Using Geometry
In the triangle formed by the center of the tube and the points where the light hits the boundaries, we can relate the angles using the sine rule. The angle ϕ is the angle of refraction at the first boundary, and θ is the angle of incidence at the second boundary. The relationship can be expressed as:
sin(ϕ)r=sin(π−θ)R
Since sin(π−θ)=sin(θ), we can rewrite this as:
sin(ϕ)r=sin(θ)R
Step 6: Substitute Values from Equations
Substituting the values of sin(ϕ) and sin(θ) from Equations (1) and (2):
1n′r=nn′R
This simplifies to:
1r=nR
Step 7: Solve for the Minimum Internal Radius
Rearranging gives:
r=Rn
Thus, the minimum internal radius r of the tube should be:
r=Rn
Conclusion
The minimum internal radius of the capillary tube required to ensure that any ray that hits the tube enters the liquid is given by:
r=Rn
We have a capillary tube made of glass with an outer radius R and filled with a liquid of refractive index n. We need to determine the minimum internal radius r of the tube such that any ray of light that strikes the tube will not enter the liquid.
The critical scenario occurs when the incident ray hits the outer surface of the tube at the steepest angle possible, which is 90∘. In this case, the ray will refract into the glass.
Using Snell's Law at the air-glass boundary:
n1sini=n2sinr
Here, n1=1 (for air), i=90∘, and n2=n′ (for glass). Thus:
1⋅sin(90∘)=n′⋅sin(ϕ)
This simplifies to:
sin(ϕ)=1n′
Let’s label this as Equation (1).
Now, we need to consider the boundary between the glass and the liquid. For total internal reflection to occur at this boundary, the angle of refraction r must be 90∘. Thus, applying Snell's Law again:
n′sin(θ)=nsin(90∘)
This simplifies to:
n′sin(θ)=n
From this, we can express sin(θ):
sin(θ)=nn′
Let’s label this as Equation (2).
In the triangle formed by the center of the tube and the points where the light hits the boundaries, we can relate the angles using the sine rule. The angle ϕ is the angle of refraction at the first boundary, and θ is the angle of incidence at the second boundary. The relationship can be expressed as:
sin(ϕ)r=sin(π−θ)R
Since sin(π−θ)=sin(θ), we can rewrite this as:
sin(ϕ)r=sin(θ)R
Substituting the values of sin(ϕ) and sin(θ) from Equations (1) and (2):
1n′r=nn′R
This simplifies to:
1r=nR
Rearranging gives:
r=Rn
Thus, the minimum internal radius r of the tube should be:
r=Rn
The minimum internal radius of the capillary tube required to ensure that any ray that hits the tube enters the liquid is given by:
r=Rn
Similar Questions
Figure shows an L-shaped tube tilled with a liquid to a height H. What should be the horizontal acceleration a of the tube so that the pressure at the point A becomes atmospheric.
View SolutionWhat should be minimum length of tube so that third resonancee can also be heard .
View SolutionA lens of refractive index n is put in a liquid of refractive index n'. If focal length of lens in air is f, its focal length in liquid will be.
View SolutionA ray of light is incident on the left vertical face of glass cube of refractive index n2, as shown in figure. The plane of incidence is the plane of the page, and the cube is surrounded by liquid (refractive index=n1). What is the largest angle of incidence θ1 for which total internal reflection occurs at the top surfaces?
View SolutionA sphere of radius R made of material of refractive index μ2 is placed in a medium of refractive index μ1. Where would an object be placed so that a real image is formed at equidistant fromk the sphere? ltbgt
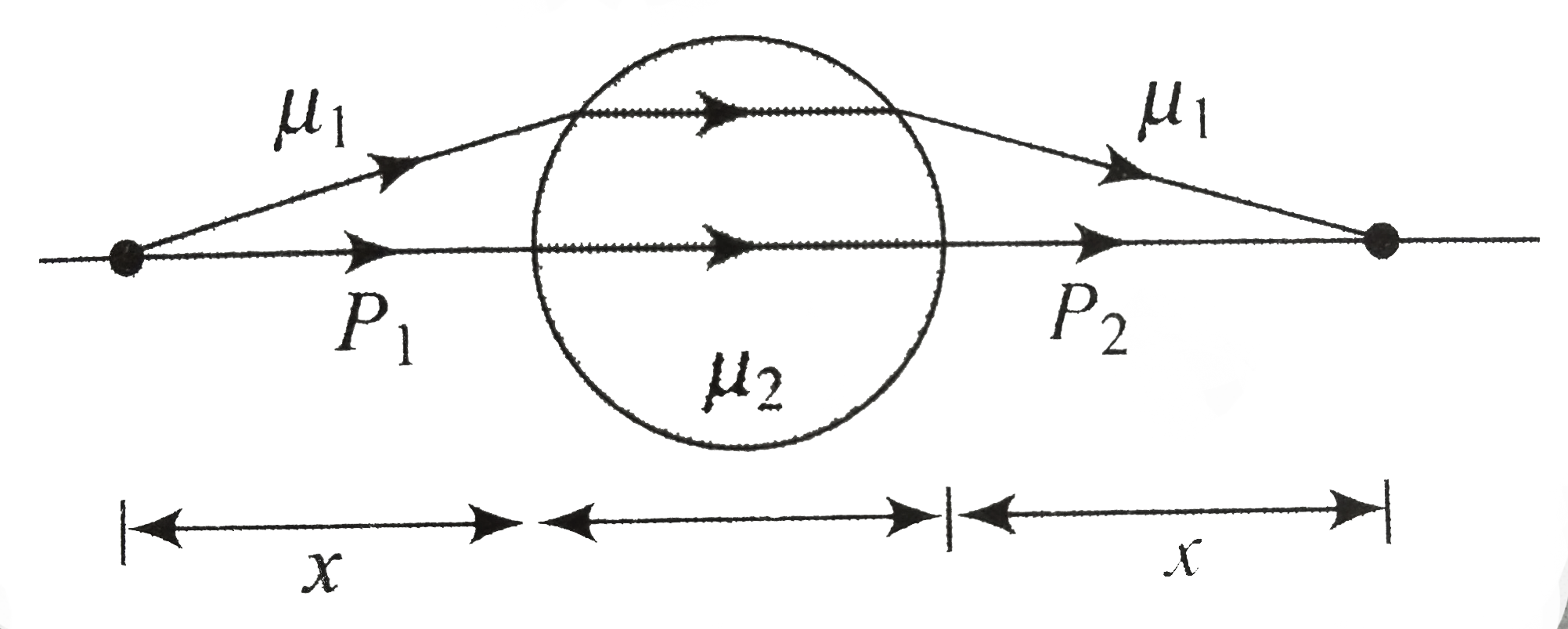View SolutionTwo capillary tubes of lengths in the ratio 2:1 and radii in the ratio 1:2 are connected in series. Assume the flow of the liquid through the tube is steady. Then, the ratio of pressure difference across the tubes is
View SolutionA cubical block of glass of refractive index n1 is in contact with the surface of water of refractive index n2. A beam of light is incident on vertical face of the block. After refraction a total internal reflection at the base and refraction at the opposite face take place. The ray emerges at angle θ as shown. The value of θ is given by
View SolutionA liquid of refractive index 1.6 is contained in the cavity of a glass specimen of refractive index 1.5 as shown in figure. If each of the curve surface has a radius of curvature of 0.20m, the arrangement obehaves as a
View SolutionWith what minimum speed v must a small ball should be pushed inside a smooth vertical tube from a heoght h so that it may reach the top of the tube? Radius of the tube is R .
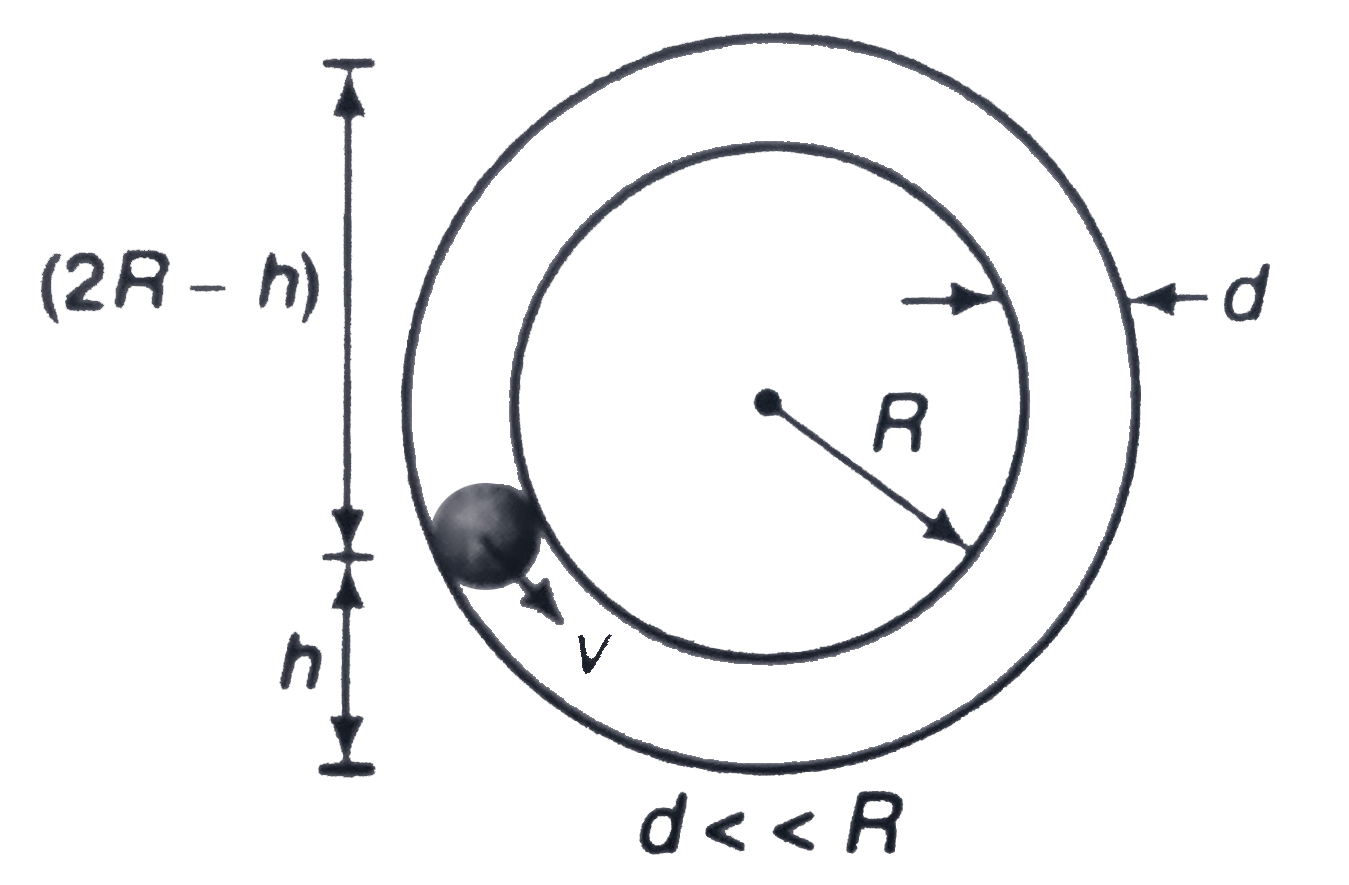View SolutionA U−tube is made up of capillaries of bores 1mm and 2mm respectively. The tube is held vertically and partically filled with a liquid of surface tension 49dyne/cm and zero contact angle. Calculate the density of the liquid of the difference in the levels of the meniscus is 1.25cm.
View Solution