A sphere of 8cm radius behaves like a black body. It is in thermal equilibrium with the surrounding and absorbs 10W of power radiated to it from surrounding. The temperature of the sphere (σ=5.67×10−8W/m2K4) is approximately.
160K
217K
283K
347K
To solve the problem, we need to find the temperature of a sphere that behaves like a black body, given that it absorbs 10 W of power from its surroundings. We will use the Stefan-Boltzmann law to relate the absorbed power to the temperature of the sphere.
1. Understand the Given Information:
- The radius of the sphere r=8 cm=0.08 m (conversion from cm to m).
- The power absorbed by the sphere P=10 W.
- The Stefan-Boltzmann constant σ=5.67×10−8 W/m2K4.
2. Calculate the Surface Area of the Sphere:
The surface area A of a sphere is given by the formula:
A=4πr2
Substituting the value of r:
A=4π(0.08)2
A=4π(0.0064)≈0.0804 m2
3. Apply the Stefan-Boltzmann Law:
According to the Stefan-Boltzmann law, the power radiated by a black body is given by:
P=σAT4
Since the sphere is in thermal equilibrium, the power absorbed is equal to the power radiated:
10=σAT4
4. Rearrange the Equation to Solve for Temperature T:
T4=PσA
Substituting the values:
T4=105.67×10−8×0.0804
5. Calculate the Denominator:
First, calculate σA:
σA=5.67×10−8×0.0804≈4.56×10−9
6. Calculate T4:
Now substitute this back into the equation for T4:
T4=104.56×10−9≈2.19×109
7. Calculate T:
Now take the fourth root to find T:
T=(2.19×109)1/4
T≈217 K
Final Answer:
The temperature of the sphere is approximately T≈217 K.
---
- The radius of the sphere r=8 cm=0.08 m (conversion from cm to m).
- The power absorbed by the sphere P=10 W.
- The Stefan-Boltzmann constant σ=5.67×10−8 W/m2K4.
The surface area A of a sphere is given by the formula:
A=4πr2
Substituting the value of r:
A=4π(0.08)2
A=4π(0.0064)≈0.0804 m2
According to the Stefan-Boltzmann law, the power radiated by a black body is given by:
P=σAT4
Since the sphere is in thermal equilibrium, the power absorbed is equal to the power radiated:
10=σAT4
T4=PσA
Substituting the values:
T4=105.67×10−8×0.0804
First, calculate σA:
σA=5.67×10−8×0.0804≈4.56×10−9
Now substitute this back into the equation for T4:
T4=104.56×10−9≈2.19×109
Now take the fourth root to find T:
T=(2.19×109)1/4
T≈217 K
The temperature of the sphere is approximately T≈217 K.
Similar Questions
Calculate the amount of radiant energy from a black body at a temperature of (i) 27∘C (ii) 2727∘C. σ=5.67×10−8Wm−2K−4.
View SolutionIf the filament of a 100 W bulb has an area 0.25cm2 and behaves as a perfect black body. Find the wavelength corresponding to the maximum in its energy distribution. Given that Stefan's constant is σ=5.67×10−8J/m2sK4.
View SolutionIf the filament of a 100 W bulb has an area 0.25cm2 and behaves as a perfect block body. Find the wavelength corresponding to the maximum in its energy distribution. Given that Stefan's constant is σ=5.67×10−8J/m2sK4.
View SolutionAc cording to Stefan' law of radiation, a black body radiates energy σT4 from its unit surface area every second where T is the surface temperature of the black body and σ=5.67×10−8W/m2K4 is known as Stefan's constant. A nuclear weapon may be thought of as a ball of radius 0.5 m When detoneted, it reachs temperature of 106K and can be treated as a black body. (a) Estimate the power it radiates. (b) if surrounding has water at 30∘C how much water can 10% of the energy produced evaporate in 1s ? [sw=4186.0J/KgKandLυ=22.6×105J/kg] (c ) If all this energy U is in the form of radiation, corresponding momentum is p=U/c. How much momentum per unit time does it impart on unit area at a distance of 1 km ?
View SolutionOne end of a rod of length 20cm is inserted in a furnace at 800K The sides of the rod are covered with an insulating material and the other end emits radiation like a black body. The temperature of this end is 750K in the steady state The temperature of the surrounding air is 300K Assuming radiation to be the only important mode of energy transfer between the surrounding and the open end of the rod, find the thermal conductivity of the rod Stefan's constant σ=6.0×10−8Wm−2K−4 .
View SolutionA spherical body of radius 10cm radiates 300W at 227°C. If the radius is doubled and temperature is remain same, the power radiated will be
View SolutionThe earth receives solor radiation at a rate of 8.2Jcm−2−1min . Assuming that the sun radiates like a blackbody, calculate the surface temperature of the sun. The angle subtended by the sun on the earth is 0.53∘ and the stefan constant σ=5.67×10−sWm−2K−4 .
View SolutionOne end of a rod length 20cm is inserted in a furnace at 800K. The sides of the rod are covered with an insulating material and the other end emits radiation like a blackbody. The temperature of this end is 750K in the steady state. The temperature of the surrounding air is 300K. Assuming radiation to be the only important mode of energy transfer between the surrounding and the open end of the rod, find the thermal conductivity of the rod. Stefan constant σ=6.0×10−1Wm−2K−4 .
View SolutionOne end of a rod length 20cm is inserted in a furnace at 800K. The sides of the rod are covered with an insulating material and the other end emits radiation like a blackbody. The temperature of this end is 750K in the steady state. The temperature of the surrounding air is 300K. Assuming radiation to be the only important mode of energy transfer between the surrounding and the open end of the rod, find the thermal conductivity of the rod. Stefan constant σ=6.0×10−1Wm−2K−4 .
View SolutionA solid body X of very large heat capacity is kept in an atmosphere whose temperature is 300 K. The body X is connected to a rod of length 1 m and cross sectional area S, as shown in the figure. Thermal conductivity of rod AB is 0.0567W/mK. Assuming that there is no heat exchange with the surrounding except fom the end B of the rod i.e., neither by any surface of X nor by the curved surface of rod. The end B has emissivity e=0.8. If the steady state temperature of the end B is 400 K then find the temperature of X in steady state. (Stefan constant σ−5.67×10−8W/m2K4)
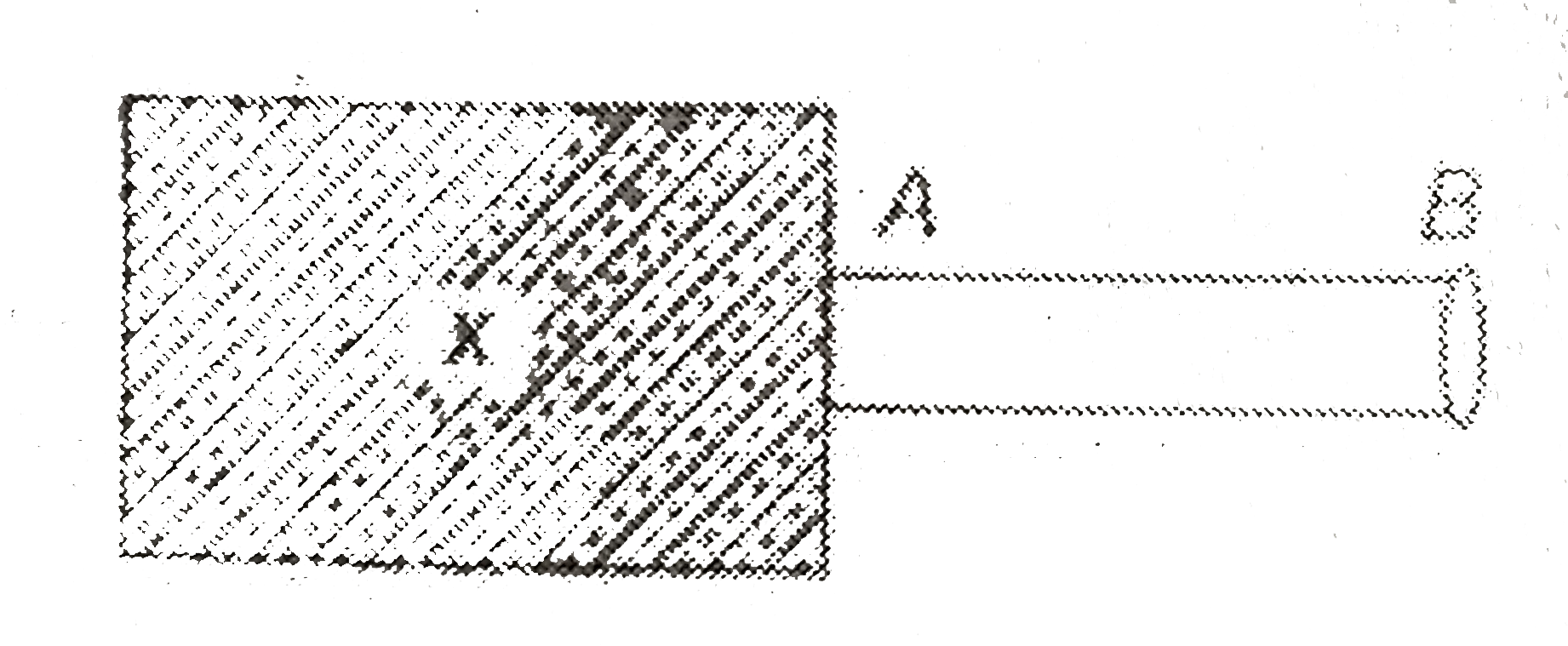
View Solution
