A square frame is made rods each of mass m and length l. The moment of inertia of the square about its face diagonal is
23ml2
13ml2
43ml2
25ml2
To find the moment of inertia of a square frame made of rods about its face diagonal, we can follow these steps:
Step 1: Understand the Geometry
The square frame consists of four rods, each of mass m and length l. The face diagonal of the square connects two opposite corners of the square.
Step 2: Identify the Moment of Inertia for One Rod
The moment of inertia I of a single rod about an axis through one end and perpendicular to its length is given by the formula:
I=13ml2
However, since we are interested in the moment of inertia about the diagonal, we need to apply the parallel axis theorem.
Step 3: Calculate the Angle
The angle θ between the rod and the diagonal is 45∘ because the diagonal bisects the right angle of the square.
Step 4: Use the Perpendicular Axis Theorem
For a rod inclined at an angle θ, the moment of inertia about the diagonal can be expressed as:
Idiagonal=Iend⋅cos2(θ)+Iend⋅sin2(θ)
Since cos2(45∘)=sin2(45∘)=12, we can simplify this to:
Idiagonal=13ml2⋅12+13ml2⋅12=13ml2
Step 5: Total Moment of Inertia for the Square Frame
Since there are four rods in the square frame, the total moment of inertia about the diagonal is:
Itotal=4⋅(13ml2⋅12)=43ml2⋅12=23ml2
Final Result
Thus, the moment of inertia of the square frame about its face diagonal is:
Idiagonal=23ml2
The square frame consists of four rods, each of mass m and length l. The face diagonal of the square connects two opposite corners of the square.
The moment of inertia I of a single rod about an axis through one end and perpendicular to its length is given by the formula:
I=13ml2
However, since we are interested in the moment of inertia about the diagonal, we need to apply the parallel axis theorem.
The angle θ between the rod and the diagonal is 45∘ because the diagonal bisects the right angle of the square.
For a rod inclined at an angle θ, the moment of inertia about the diagonal can be expressed as:
Idiagonal=Iend⋅cos2(θ)+Iend⋅sin2(θ)
Since cos2(45∘)=sin2(45∘)=12, we can simplify this to:
Idiagonal=13ml2⋅12+13ml2⋅12=13ml2
Since there are four rods in the square frame, the total moment of inertia about the diagonal is:
Itotal=4⋅(13ml2⋅12)=43ml2⋅12=23ml2
Thus, the moment of inertia of the square frame about its face diagonal is:
Idiagonal=23ml2
Similar Questions
A square is made by joining four rods each of mass M and length L. Its moment of inertia about an axis PQ, in its plane and passing through one of its corner is
 View Solution
View Solution
A square is made by joining four rods each of mass M and length L. Its moment of inertia about an axis PQ, in its plane and passing through one one of its corner isView Solution
Knowledge Check
- Question 1 - Select One
Two masses each of mass M are attached to the end of a rigid massless rod of length L. The moment of interia of the system about an axis passing centre of mass and perpendicular to its length is.
AML2/4BML2/2CML2D2ML2

A square is made by joining four rods each of mass M and length L. Its moment of inertia about an axis PQ, in its plane and passing through one one of its corner isView SolutionFour identical thin rods each of mass M and length l, from a square frame. Moment of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is
View SolutionTwo uniform rods each of mass M and length L are joined as shown in the figure. The moment of inertia of the system about line AB is kML2.Find the value of k.
View SolutionA square plate of mass M and edge L is shown in the figure. The moment of inertia of the plate about the axis in the plane of plate and passing through one of its vertex making an angle 15∘ horizontal is
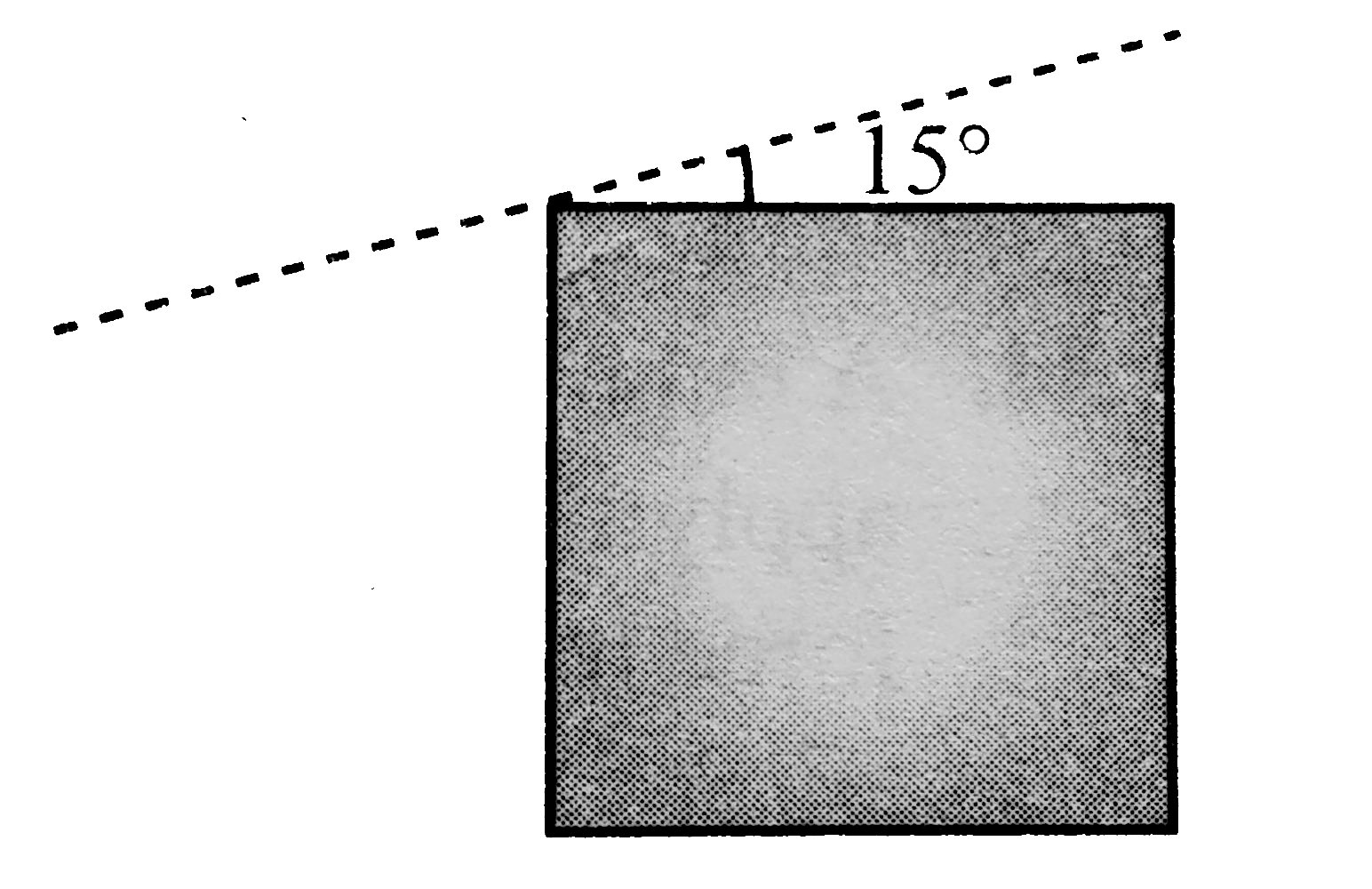 View Solution
View SolutionFour thin rods each of mass m and length l are joined to make a square. Find moment of inertia of all the four rods about any side of the square.
View SolutionA thin uniform wire of mass m and length l is bent into to shape of a semicircle. The moment of inertia of that wire about an axis passing through its free ends is
View SolutionFour solid sphereas each of diameter √5cm and mass 0.5kg are placed with their centres at the corners of a square of side 4cm. The moment of inertia of the system about the diagonal of the square is N×10−4kg−m2, the N is -
View Solution

