In the figure shown surfaces are smooth and blocks A and B have same mass m. The two bodies are displaced right and released. It is found that bodies move according to the equation xA=Asin(ωt+ϕ), XB=2Asin(ωt+ϕ)

K1K2=32
K1K2=12
K1K2=1
K1K2=2
K2A=ω2(2A)
K1A−K2A=ω2A
⇒K2K1−K2=21
⇒K1K2=32
Similar Questions
A particle moves on the X-axis according to the equation x=x0sin2ωt. The motion simple harmonic
View SolutionA particle moves on the X-axis according to the equation x=5sin2ωt. The motion simple harmonic
View SolutionIn the figure shown A and B are free to move . All the surface are smooth. Mass of Aism. Then
View SolutionA particle moves along x-axis according to relation x=1+2sinωt. The amplitude of S.H.M. is
View SolutionA wave is propagating in positive x−direction. A time t=0 its snapshot is taken as shown. If the wave equation is y=Asin(ωt−Kx+ϕ), then ϕ is
_2019_CBT7_E01_013_Q01.png)
View SolutionA wave is propagating in positive x−direction. A time t=0 its snapshot is taken as shown. If the wave equation is y=Asin(ωt−Kx+ϕ), then ϕ is
_2019_CBT7_E01_013_Q01.png)
View Solution
Figure shown two blocks A and B connected to an ideal pulley string system. In this system when bodies are released then:(neglect friction and takeg=10ms2)
View SolutionThe blocks A and B shown in figure have masses MA=5kg and MB=4kg. The system is released from rest. The speed of B after A has travelled a distance 1m along the incline is
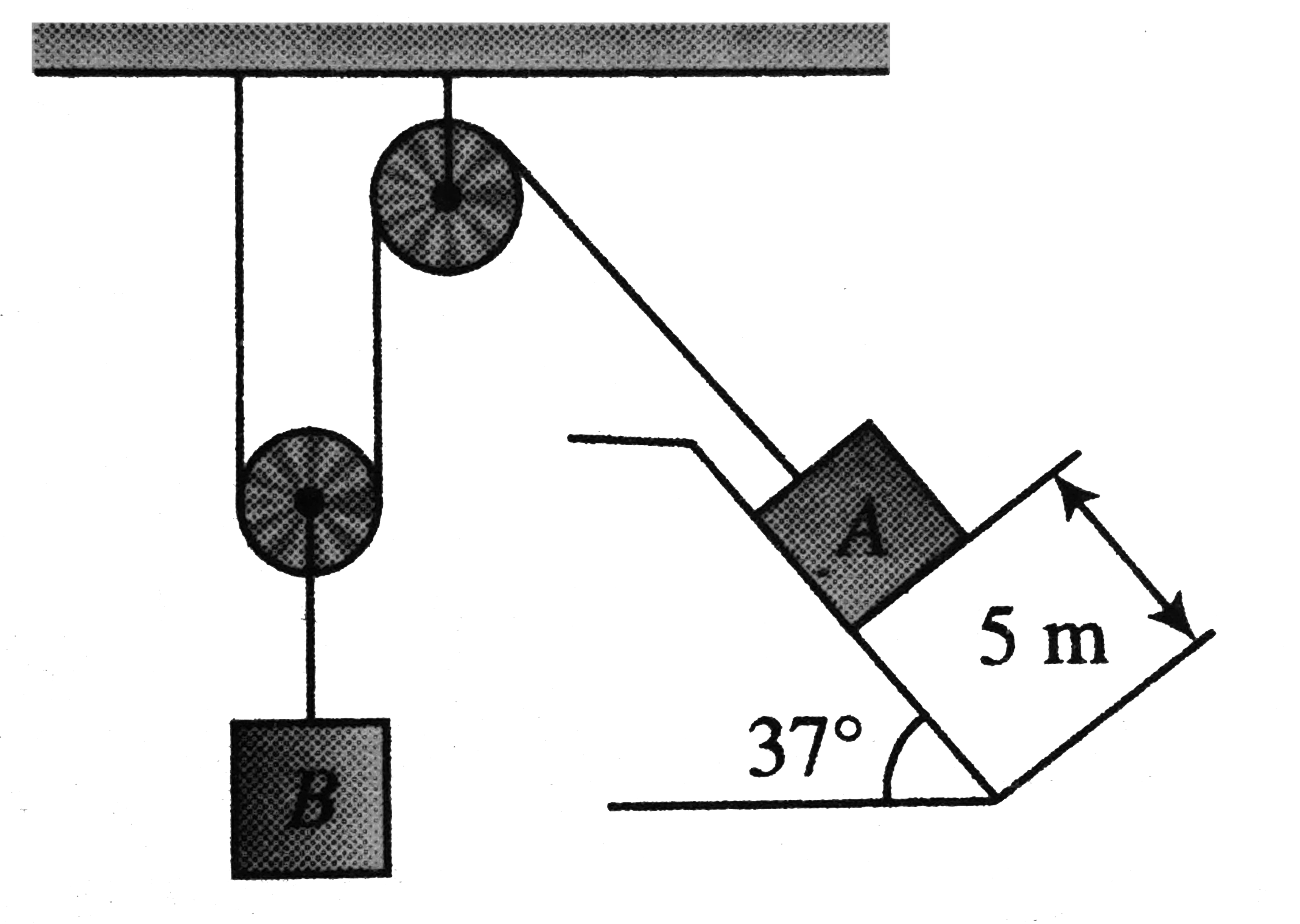
View SolutionIn the adjoining figure, block A is of mass (m) and block B is of mass2 m. The spring has force constant k. All the surfaces are smooth and the system is released form rest with spring unstretched.
 .
.
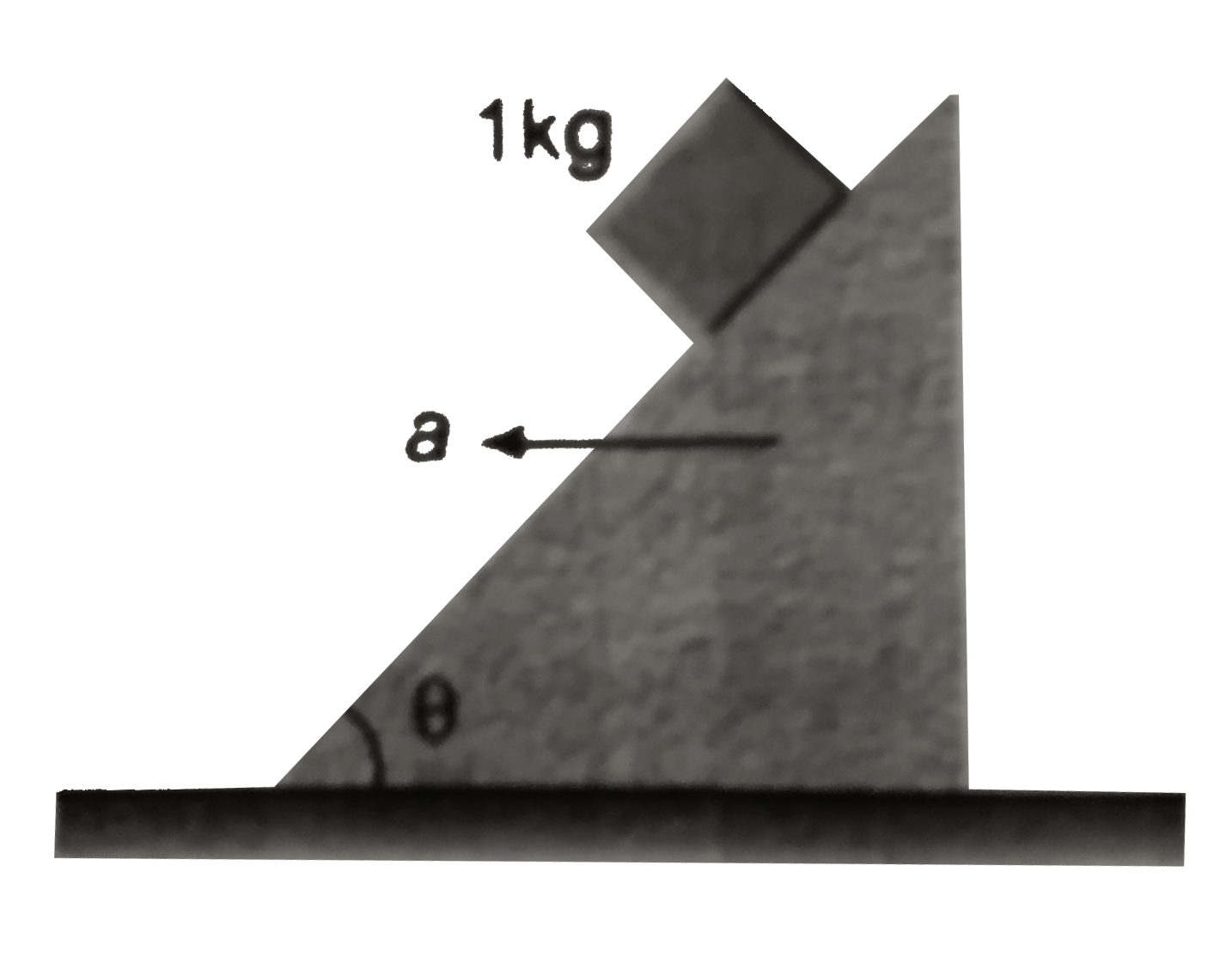
View SolutionTwo blocks A and B each of equal masses m are rleased from the top of a smooth fixed wedge as shown in the figure. Find the magnitude of the accelertion of the centre of mass of the two blocks.

View Solution
