Suppose 0.5 moles of an ideal gas undergoes an isothermal expansion as energy is added to it as heat Q. graph shows the final volume Vf versus Q. the temperature of the gas is (use In9=2 and R=253J/mol−K)
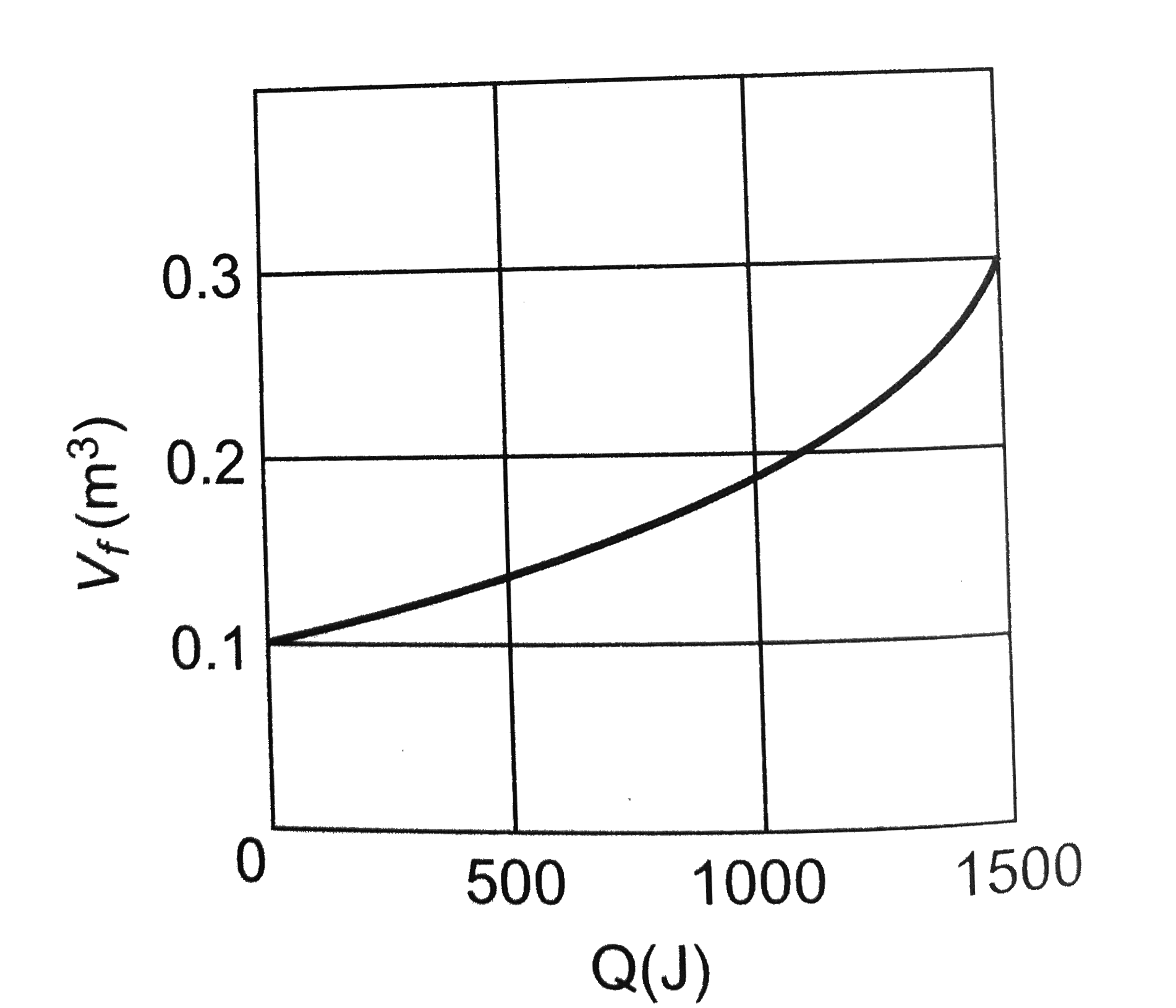
360K
260K
390K
490K
Step by step video & image solution for Suppose 0.5 moles of an ideal gas undergoes an isothermal expansion as energy is added to it as heat Q. graph shows the final volume V_(f) versus Q. the temperature of the gas is (use In 9 = 2 and R = (25)/(3) J//mol-K) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
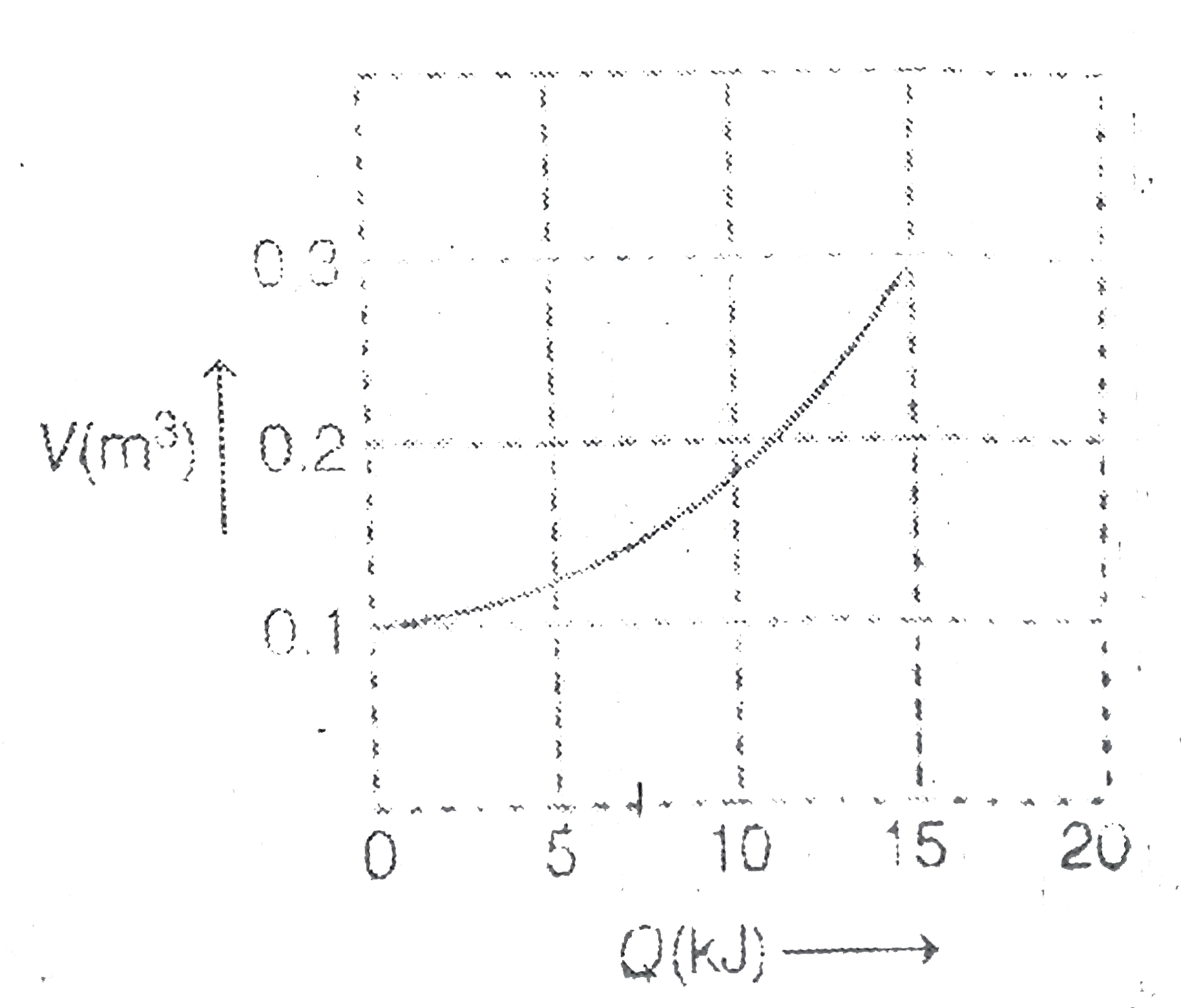
Consider isothermal expansion of 0.5 mole of an ideal gas when Q amount of heat is added to it. Following graph shows variation in volume V with Q. Find the temperature of the gas
(ln 3≈10,R=253J/mole−K)
View SolutionOne mole of an ideal gas undergoes a process
P=P0−αV2
where α and P0 are positive constant and V is the volume of one mole of gas
Q. When temperature is maximum, volume is
View Solution
Knowledge Check
One mole of an ideal monoatomic gas at temperature T0 expands slowly according to the law pV = constant. If the final temperature is 2T0, heat supplied to the gas is
A2RT0BRToC32RT0D12RT0One mole of an ideal monatomic gas at temperature T0 expands slowly according to the law PV=constant.If the final temperature is 2T0, heat supplied to the gas is
A2RT0BRT0C32RT0D12RT0One mole of an ideal monoatomic gas at temperature T0 expands slowly according to the law pV = constant. If the final temperature is 2T0, heat supplied to the gas is
Aa.2RT0Bb.RT0Cc.32RT0Dd.12RT0
One mole of an ideal gas undergoes a process
P=P0−αV2
where α and P0 are positive constant and V is the volume of one mole of gas
Q. When temperature is maximum, volume is
View SolutionIn figure, a sample of 3 moles of an ideal gas is undergoing through a cyclic process ABCA.A total of 1500J of heat is withdraw from the sample in the process. The work done by the gas during the part BC is −PKJ.FINDP.(R=253J/moleK)

View SolutionOne mole of an ideal monoatomic gas at temperature T0 expands slowly according to the law pV = constant. If the final temperature is 2T0, heat supplied to the gas is
View SolutionOne mole of an ideal gas undergoes a process
P=P0−αV2
where α and P0 are positive constant and V is the volume of one mole of gas
Q. The maximum attainable temperature is
View SolutionAt 27∘C two moles of an ideal monatomic gas occupy a volume V. The gas expands adiabatically to a volume 2V. Calculate
(a) final temperature of the gas
(b) change in its internal energy and
[ R=8.31J/mol−K]
View Solution
