Statement-1 : A conducting rod is given a velocity v subsequently the rod slides on the smooth conducting rails in horizontal plane. The magnetic field is perpendicular to the plane of figure.
Statement-2 : In the above situation energy lost by rod will be equal to work done by magnetic force.
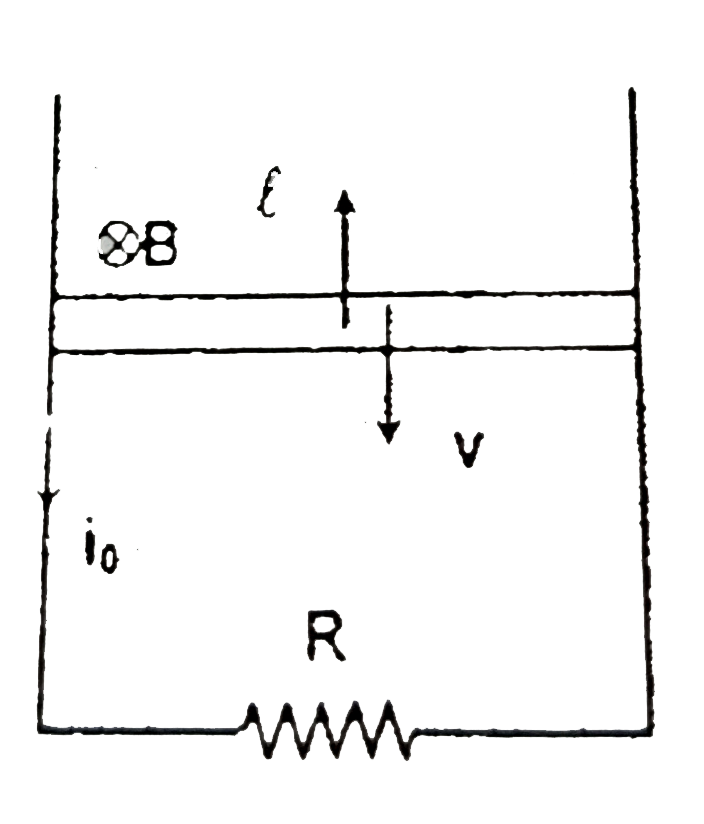
Statement-1 is True, Statement-2 is True, Statement-2 is a correct explantion for Statement-1
Statement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explantion for Statement-1
Statement-1 is True, Statement-2 is False
Statement-1 is False, Statement-2 is True.
Step by step video & image solution for Statement-1 : A conducting rod is given a velocity v subsequently the rod slides on the smooth conducting rails in horizontal plane. The magnetic field is perpendicular to the plane of figure. Statement-2 : In the above situation energy lost by rod will be equal to work done by magnetic force. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A conducting wire xy of lentgh l and mass m is sliding without friction on vertical conduction rails ab and cd as shown in figure. A uniform magnetic field B exists perpendicular to the plane of the rails, x moves with a constant velocity of

View SolutionA conducting wire xy of lentgh l and mass m is sliding without friction on vertical conduction rails ab and cd as shown in figure. A uniform magnetic field B exists perpendicular to the plane of the rails, x moves with a constant velocity of

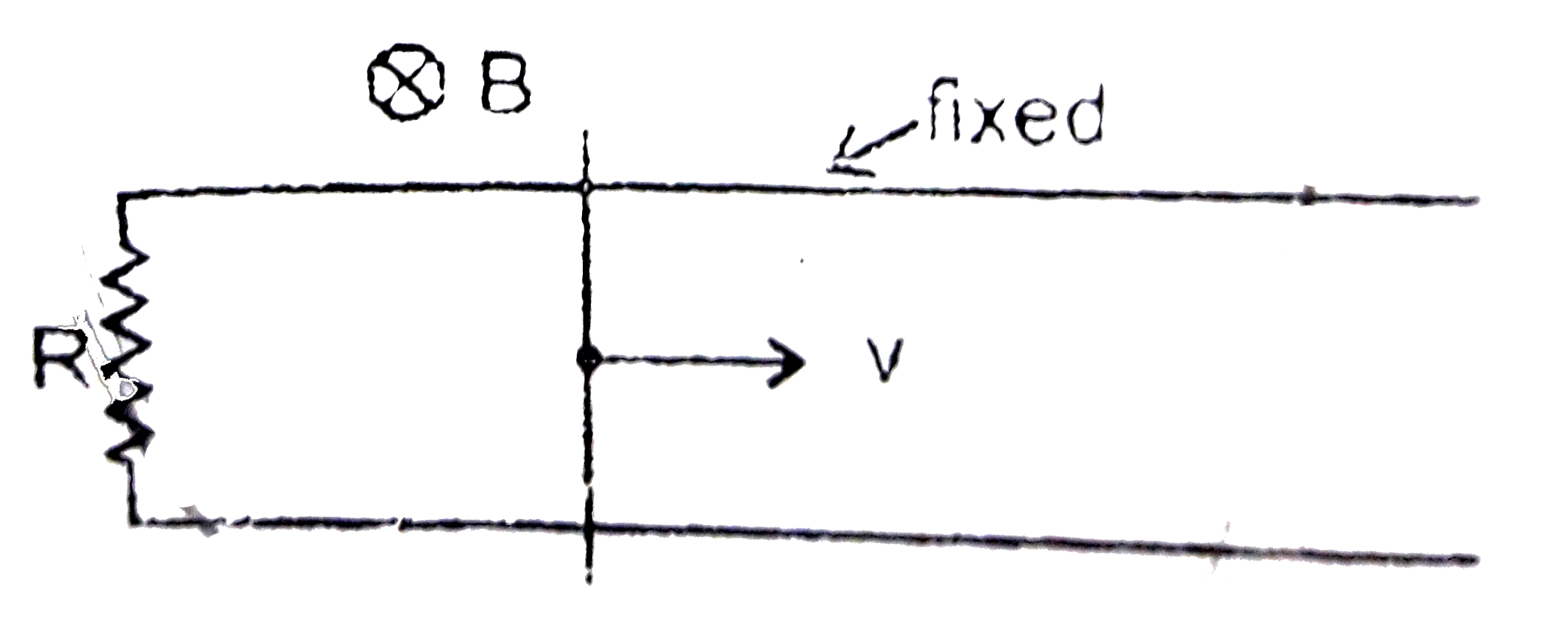
View SolutionStatement I: A resistance R is connected between the two ends of the parallel smooth conducting rails. A conducting rod lies on these fixed horizontal rails and a uniform constant magnetic field B exists perpendicular to the plane of the rails as shown in Fig. if the rod is given a velocity υ and released as shown in Fig. 3.188, it will stop after some time. the total work done by magnetic field negative.

Statement II: If force acts opposite to direction of velocity its work done is negative.
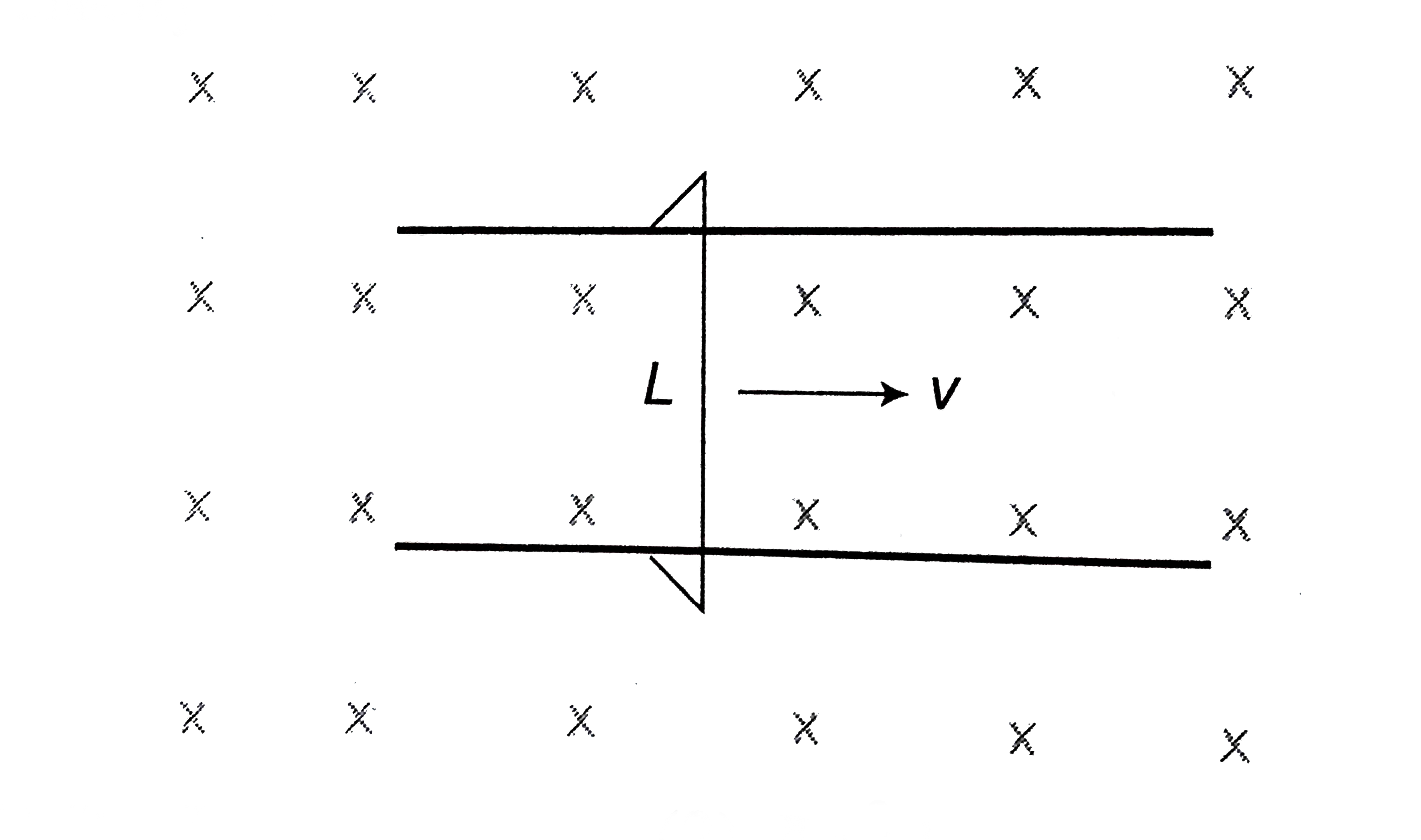
View SolutionShows a wire sliding on two parallel, conducting rails placed at a separaton l. A magnetic feld B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constatn velocity v ?

View SolutionFigure shows a wire sliding on two parallel, conducting rails placed at a separation L . A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity V ?
View SolutionA resistance R is connected between the two ends of the parallel smooth conducting rails.A conducting rod lies on these fixed horizontal rails and a uniform constant magnetic field B exists perpendicular to the plane of the rails as shown in the figure.If the rod is given a velocity v and released as shown in figure, it will stop after some time, which option are correct:
View SolutionA conducting rod of length L slides at a constant velocity V on two parallel conducting rails as shown in figure. The mechanical power required to pull the rod at constant velocity is

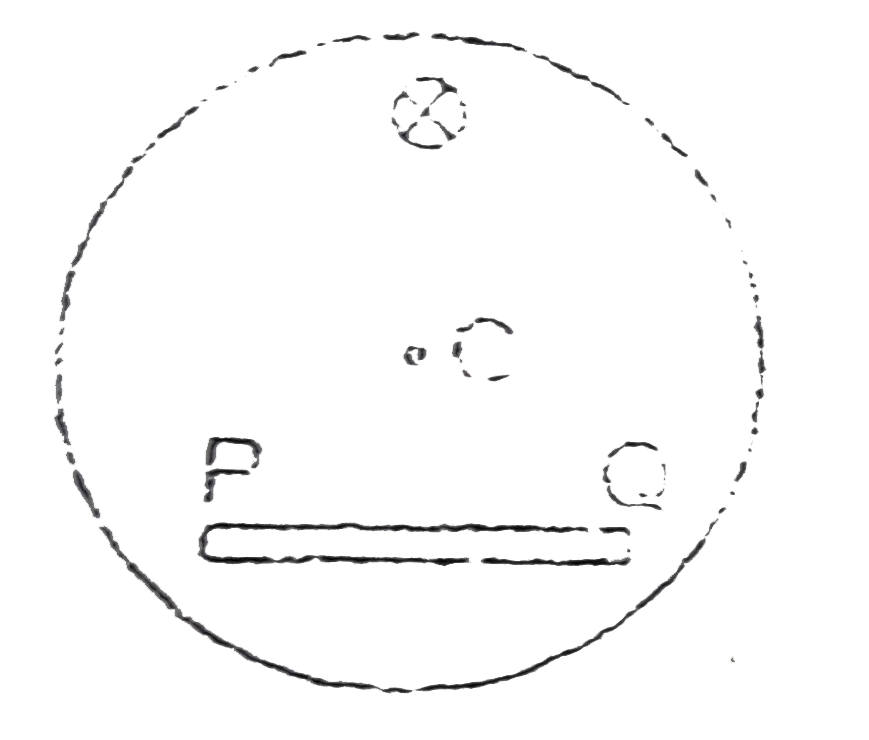
View SolutionIn a cylindrical region uniform magnetic field which is perpendicular to the plane of the figure is in increasing with time and a conducting rod PQ is placed in the region.If C is the centre of the circle then
View SolutionA conducting rod of mass m and length l is placed over a smooth horizontal surface. A uniform magnetic field B is acting perpendicular to the rod. Charge q is suddenly passed through the rod and it acquires an initial velocity v on the surface, then q is equal to
View SolutionA U - shaped conducting frame is fixed in space. A conducting rod CD lies at rest on the smooth frame as shown. The frame is in a uniform magnetic field B0 which is perpendicular to be plane of the frame . At the time t = 0 , the magnitude of the magnetic field being to change with time t as, B=B01+kt , where k is a positive constant . For no current to be ever induced in the frame the speed with which rod should be pulled starting from time t = 0 is (the rod CD should be moved such that its velocity must lie in the plane of frame and perpendicular to rod (CD)
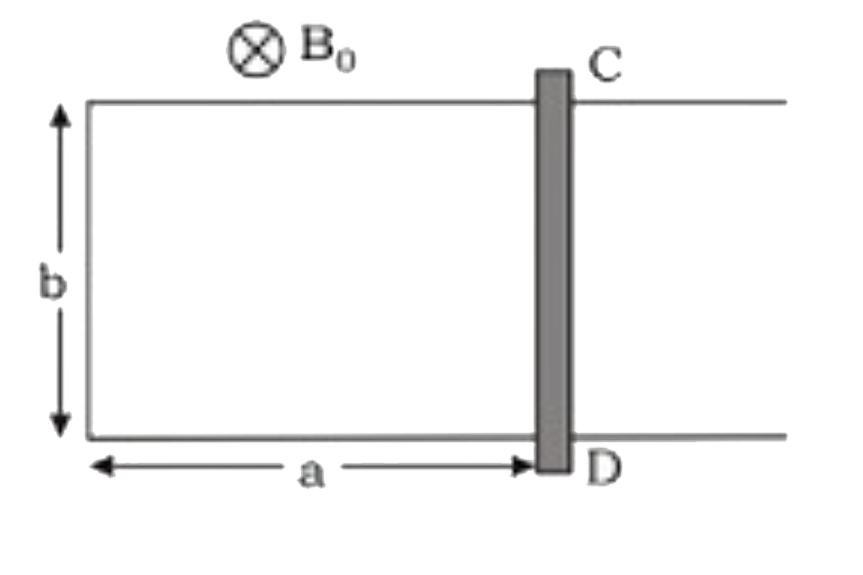
View Solution
