Statement-1 : Standing wave of small amplitude is generated on a string. The kinetic energy of any small section of string will be same as its potential energy.
Statement-2 : A standing wave can be written as superposition of two travelling waes. For a wave of small amplitude travelling on string, kinetic energy of any string element is equal to its potential energy at any instant.
Statement-1 is True, Statement-2 is True, Statement-2 is a correct explantion for Statement-1
Statement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explantion for Statement-1
Statement-1 is True, Statement-2 is False
Statement-1 is False, Statement-2 is True.
To analyze the given statements and determine their correctness, we will break down the concepts of standing waves, kinetic energy, and potential energy in a string.
1. Understanding Standing Waves:
- A standing wave is formed by the superposition of two traveling waves moving in opposite directions. This results in nodes (points of no displacement) and antinodes (points of maximum displacement) along the string.
2. Kinetic Energy of a Small Section of String:
- The kinetic energy (KE) of a small segment of the string can be expressed as:
KE=12μ(∂y∂t)2Δx
where μ is the linear mass density of the string, ∂y∂t is the velocity of the string segment, and Δx is a small length of the string.
3. Potential Energy of a Small Section of String:
- The potential energy (PE) stored in the string due to its tension can be expressed as:
PE=12T(∂y∂x)2Δx
where T is the tension in the string and ∂y∂x is the slope of the string.
4. Relating Kinetic and Potential Energy:
- For a wave of small amplitude, the kinetic energy and potential energy can be shown to be equal at any instant. This is because, at any point in time, the energy oscillates between kinetic and potential forms, maintaining a balance.
5. Superposition Principle:
- The statement that a standing wave can be written as a superposition of two traveling waves is correct. The resultant wave can be expressed mathematically, confirming that the energy distribution will also reflect this relationship.
6. Conclusion:
- Both statements are true. Statement-1 correctly states that the kinetic energy of a small section of the string will equal its potential energy at any instant for small amplitude waves. Statement-2 correctly explains the principle of superposition and its implications for energy distribution in standing waves.
Final Answer:
Both Statement-1 and Statement-2 are true, and Statement-2 provides the correct explanation for Statement-1.
- A standing wave is formed by the superposition of two traveling waves moving in opposite directions. This results in nodes (points of no displacement) and antinodes (points of maximum displacement) along the string.
- The kinetic energy (KE) of a small segment of the string can be expressed as:
KE=12μ(∂y∂t)2Δx
where μ is the linear mass density of the string, ∂y∂t is the velocity of the string segment, and Δx is a small length of the string.
- The potential energy (PE) stored in the string due to its tension can be expressed as:
PE=12T(∂y∂x)2Δx
where T is the tension in the string and ∂y∂x is the slope of the string.
- For a wave of small amplitude, the kinetic energy and potential energy can be shown to be equal at any instant. This is because, at any point in time, the energy oscillates between kinetic and potential forms, maintaining a balance.
- The statement that a standing wave can be written as a superposition of two traveling waves is correct. The resultant wave can be expressed mathematically, confirming that the energy distribution will also reflect this relationship.
- Both statements are true. Statement-1 correctly states that the kinetic energy of a small section of the string will equal its potential energy at any instant for small amplitude waves. Statement-2 correctly explains the principle of superposition and its implications for energy distribution in standing waves.
Both Statement-1 and Statement-2 are true, and Statement-2 provides the correct explanation for Statement-1.
Similar Questions
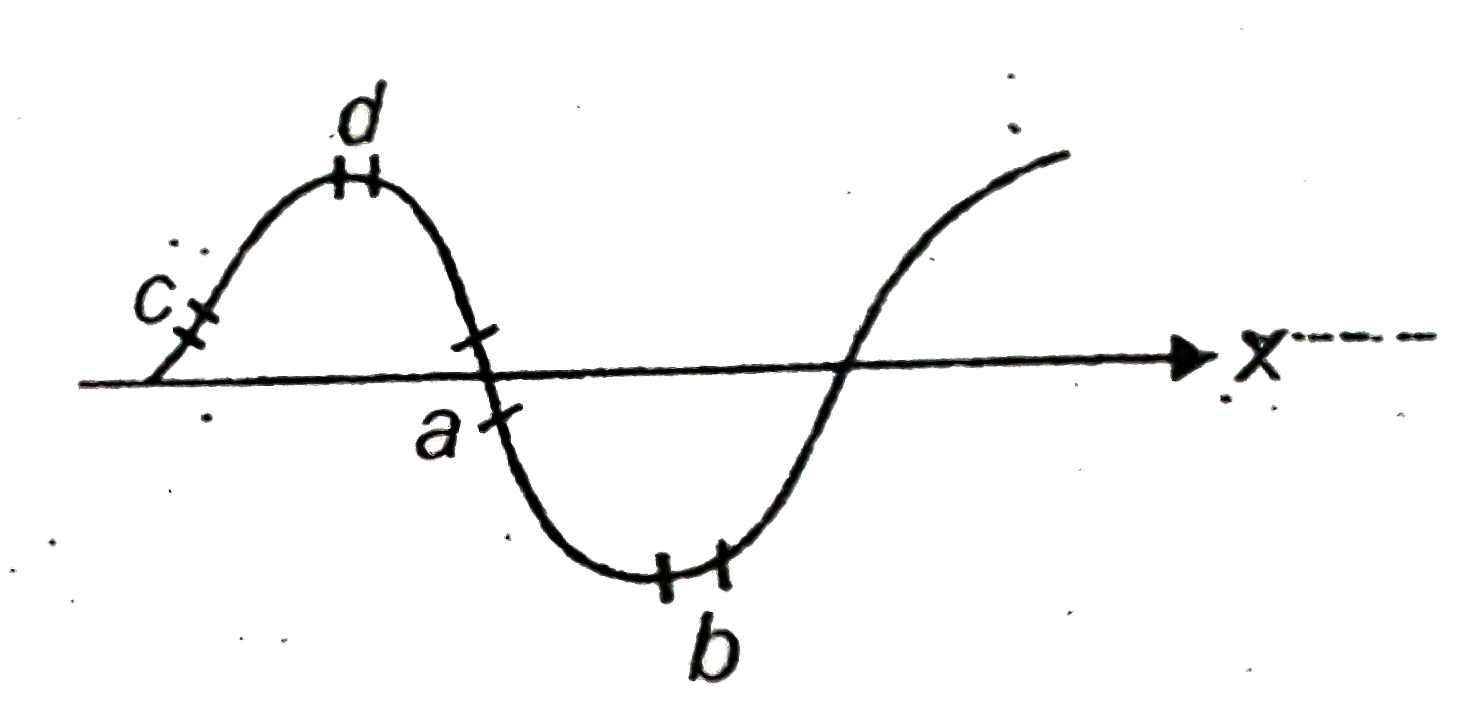
The figure shows the snapshot of a travelling sine wave in a string. Four elemental portions a,b,c and d are indicated on the string. The elemental portion with maximum potential energy is/are
View SolutionStatement-1 : in standing wave average rate of transfer of energy at any cross-section is zero.
because
Statement-2 : instantaneous rate of energy transfer at node is equal to zero.
View Solution
Knowledge Check
The equation of a wave travelling in a string can be written as y=3cosπ(10t−x). Its wavelength is
A100 cmB2 cmC5 cmDnone of the above
A standing wave arises on a string when two waves of equal amplitude , frequency and wavelength travelling in opposite superimose. If the frequency of oscillation of the standing waves
View SolutionStatement-1: Standing waves can not be obtained in air if the interfering waves are of diffeerent amplitudes.
Statement-2: In a stationary wave, different particles in a loop have different amplitudes but same phase.
View SolutionStatement-1: kinetic energy of SHM at mean position is equal to potential energy at ends for a particle moving in SHM.
Statement-2: Total energy in SHM is conserved.
View SolutionIn case of mechanical wave a particle oscillates and during oscillation its kinetic energy and potential energy changes.

View SolutionA particle executes linear SHM with amplitude A and mean position is x=0. Determine position of the particle where potential energy of the particle is equal to its kinetic energy.
View SolutionA standing wave pattern of maximum amplitude 2 mm is obtained in a string whose shape at t = 0 is represented in the graph.
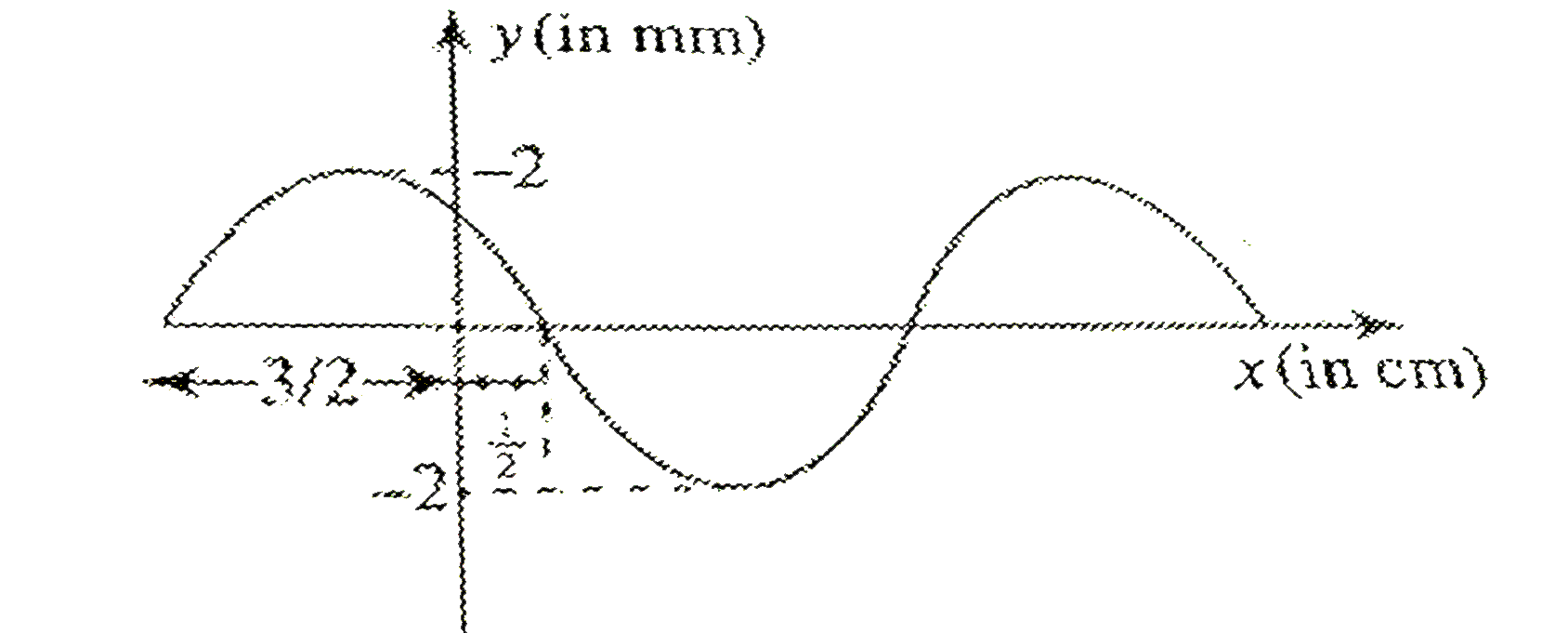
If the speed of the travelling wave in the string is 5 cm/s, then find the component waves.
View SolutionString-1 is connected with string-2. The mass per unit length in string-1 is μ1 and the mass per unit length in string-2 is 4μ1. The tension in the strings is T. A travelling wave is coming from the left. What fraction of the energy in the incident wave goes into string-2 ?

View Solution
