Question

Uranium ${}_{92}^{238}U$ is an unstable nucleaus. It decays to Thorium ${}_{90}^{234}Th$, which is again an unstable nuclei which further decays to ${}_{91}^{234}Pa$. Such decay is called successive dlsntegration. Let ${}_{92}^{238}U$ is called as $A$ of decay constant ${\lambda }_1$ and ${}_{90}^{234}Th$ is called as $B$ of decay constant ${\lambda }_2$ and stable nuclei ${}_{91}^{234}Pa$ is named as $C$. Here $A$ is called parent nucleus and $B$ is called daughter nucleus of $A$. Any two adjacent nuclei may be consider parem daughter nuclei. Suppose $N_1$, $N_2$ and $N_3$ are number of nuclei $A$, $B$ and $C$ respectively at time $t$ which undergoes decay. Then we can write
$A\stackrel{{\lambda }_2}{\to }B\stackrel{{\lambda }_2}{\to }C$
Rate of disintegration of $A=\frac{d{N}_1}{dt}=-{\lambda }_1{N}_1$
Rate of disintegration of $B=-{\lambda }_2{N}_2$ and net rate of formation of $B=\frac{d{N}_2}{dt}={\lambda }_1{N}_1-{\lambda }_2{N}_2$
Rate of formation of nuclei $C$ is equal to $\frac{d{N}_3}{dt}={\lambda }_2{N}_2$
If at $t=0$, there are $N_0$ number of nuclei of $A$, where as nuclei $B$ and $C$ are absent in the sample answer the following questions
The graph between $N_1$, $N_2$ & $N_3$ with time can be best represented by

Options

A.
B.
C.
D.

Explanation

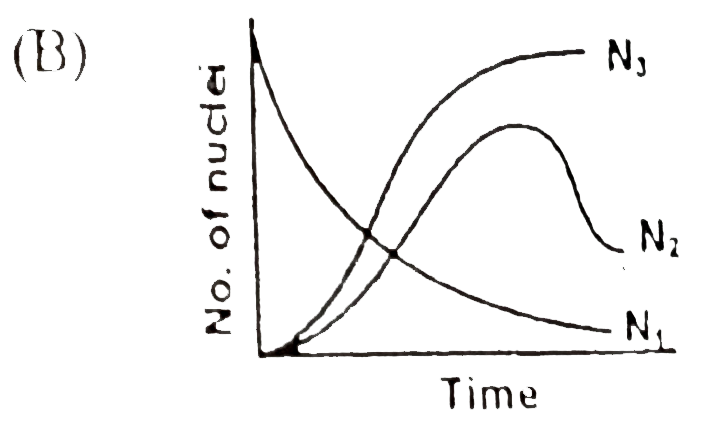
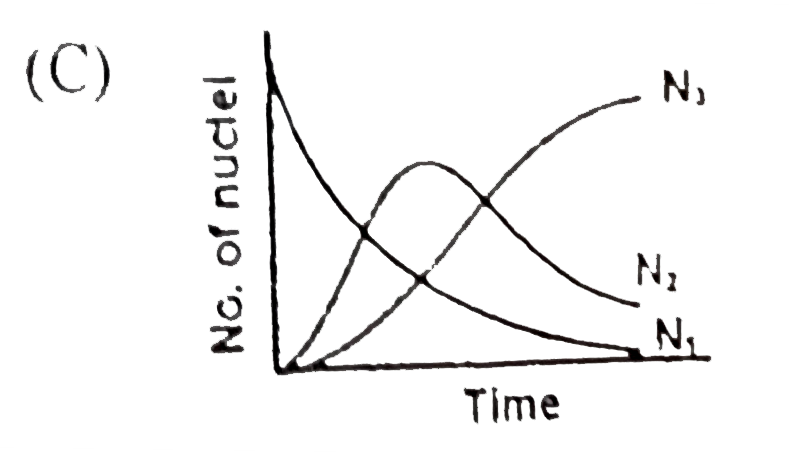
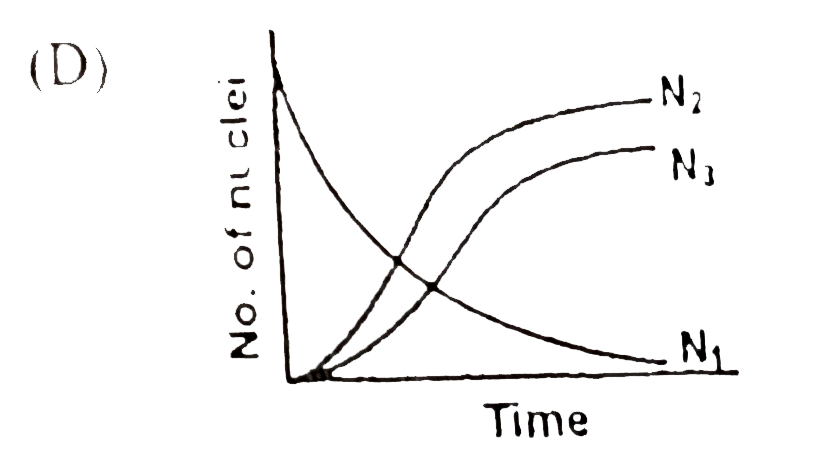
To analyze the decay of Uranium-238 to Thorium-234 and then to Protactinium-234, we will derive the equations governing the number of nuclei over time and sketch the graphs for $$N_1$$, $$N_2$$, and $$N_3$$.

Step 1: Write the equations for the decay of A
The decay of Uranium-238 (denoted as \(A\)) can be described by the equation:
\( \frac{dN_1}{dt} = -\lambda_1 N_1 \)
where \(N_1\) is the number of Uranium-238 nuclei at time \(t\) and \(\lambda_1\) is the decay constant for Uranium-238.

Step 2: Solve the equation for \(N_1\)
Integrating the equation, we have:
\( \int \frac{dN_1}{N_1} = -\lambda_1 \int dt \)
This gives:
\( \ln N_1 = -\lambda_1 t + C \)
At \(t = 0\), \(N_1 = N_0\) (the initial number of nuclei), so:
\( C = \ln N_0 \)
Thus, we can express \(N_1\) as:
\( N_1 = N_0 e^{-\lambda_1 t} \)

Step 3: Write the equations for the decay of B
The rate of formation of Thorium-234 (denoted as \(B\)) is given by:
\( \frac{dN_2}{dt} = \lambda_1 N_1 - \lambda_2 N_2 \)
where \(N_2\) is the number of Thorium-234 nuclei and \(\lambda_2\) is its decay constant.

Step 4: Substitute \(N_1\) into the equation for \(N_2\)
Substituting \(N_1\) into the equation for \(N_2\):
\( \frac{dN_2}{dt} = \lambda_1 N_0 e^{-\lambda_1 t} - \lambda_2 N_2 \)

Step 5: Solve the differential equation for \(N_2\)
This is a first-order linear differential equation. To solve it, we can use an integrating factor:
\( \mu(t) = e^{\int \lambda_2 dt} = e^{\lambda_2 t} \)
Multiplying through by the integrating factor:
\( e^{\lambda_2 t} \frac{dN_2}{dt} + \lambda_2 e^{\lambda_2 t} N_2 = \lambda_1 N_0 e^{(\lambda_2 - \lambda_1)t} \)
Integrating both sides will yield \(N_2\) as a function of time.

Step 6: Write the equation for the formation of C
The rate of formation of Protactinium-234 (denoted as \(C\)) is given by:
\( \frac{dN_3}{dt} = \lambda_2 N_2 \)
This means that as \(N_2\) increases, \(N_3\) will also increase.

Step 7: Analyze the graphs
- For \(N_1\): The graph will show an exponential decay starting from \(N_0\).
- For \(N_2\): Initially, \(N_2\) is zero, it will rise as \(N_1\) decays, but eventually, it will decline as \(N_2\) decays to \(N_3\).
- For \(N_3\): This will start from zero and will rise as \(N_2\) decays into \(N_3\).

Step 8: Sketch the graphs
- \(N_1\) will decrease exponentially.
- \(N_2\) will increase initially, reach a peak, and then decrease.
- \(N_3\) will start from zero and increase, eventually overtaking \(N_2\).

Conclusion
The correct representation of the graphs will show \(N_1\) decreasing, \(N_2\) increasing to a peak and then decreasing, and \(N_3\) starting from zero and increasing. The correct option that matches this description is option C.