The potential energy of the system of two identically charged spheres as shown in the figures is equal to (Assume the charge distribution to be uniform)
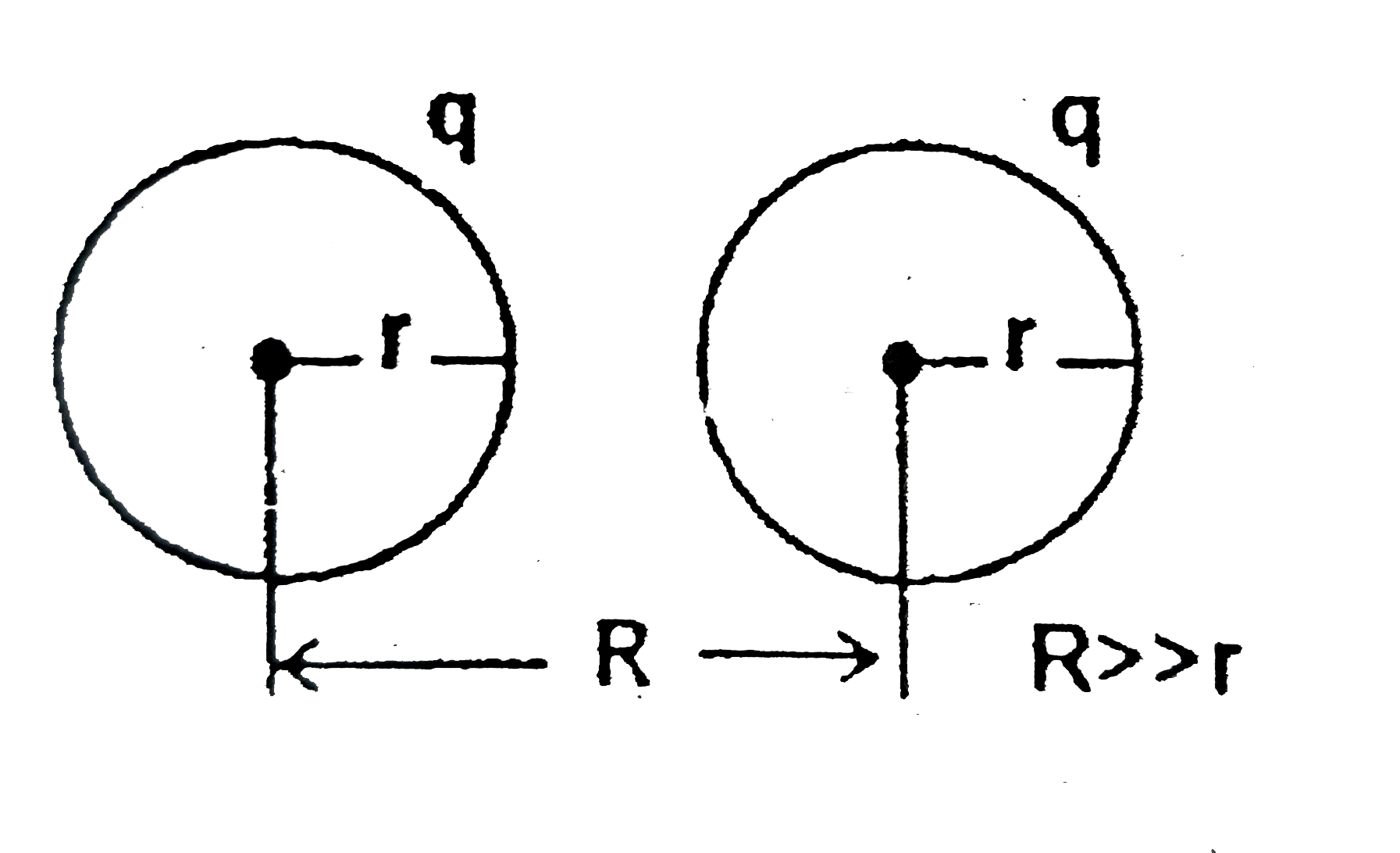
q24πε0(1R+1r)s
14πε0q2r
14πε0q2r(R+r)
None of these
Each of the charged sphere will have potential energy due to its own charge or self energy
U1=18πε0q2r.
The mutual potential energy stored in one sphere in the electric field of the other is q1q24πε0r12=U2
⇒U2=14πε0q2R
Therefore the P.E. stored in the system of spheres is
U=2U1+U2=q24πε0[1R+1r]
∴(A)
Similar Questions
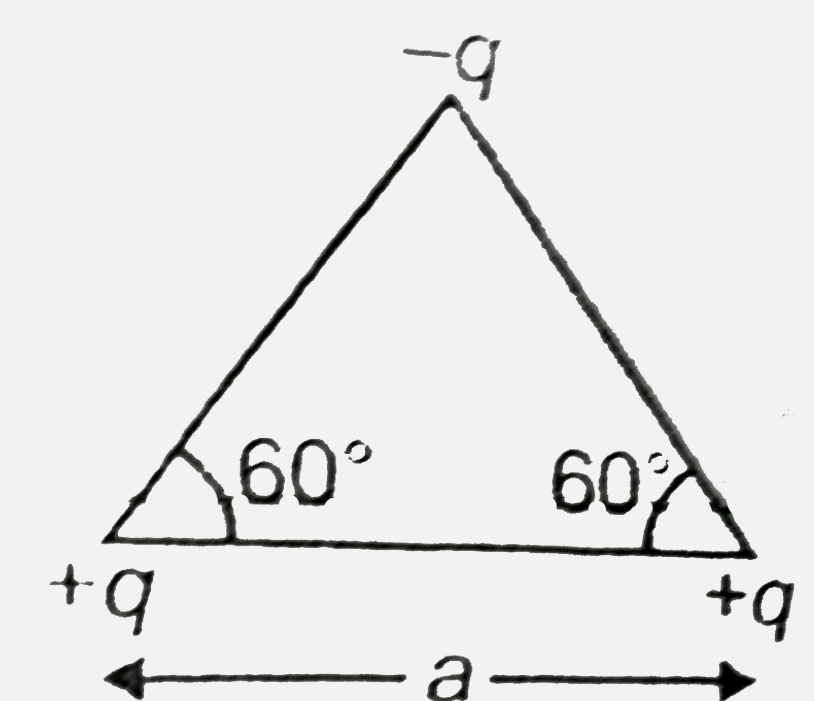
Find the electrostatic potential energy of the system shown in the figure
View SolutionFind the electric potential energy of the system of charges
View SolutionWhat is the potential energy of dipole with charge particles system as shown in (Fig. 3.96) ?
 .
.
View SolutionWhat is the potential energy of the charge and dipole system shown in (Fig. 3.93) ?
 .
.
View SolutionBoth the ring and the conducting sphere are given the same charge Q. Determine the potential of the sphere. Assume that the centre of the sphere lies on the axis of th ring. Is it necessary that the charge on the ring be uniformly distributed to answer the above question ?
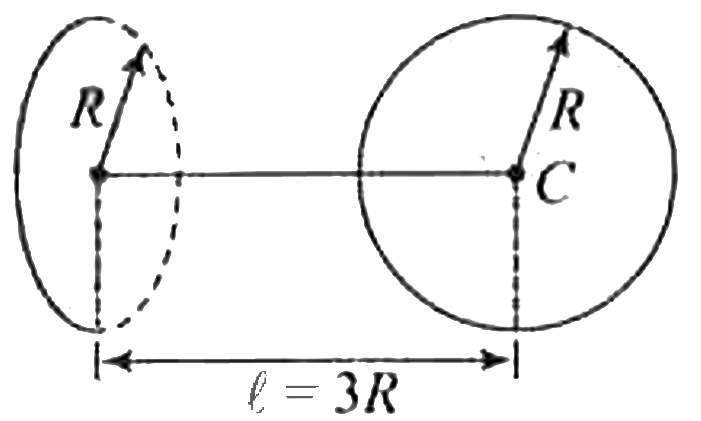
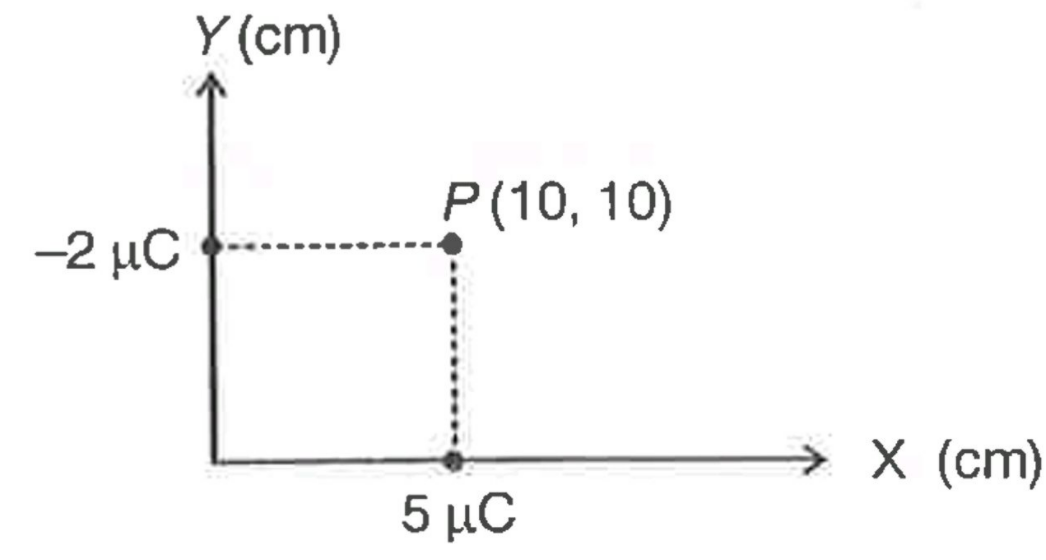
View SolutionTwo charges are placed s shown in figure below. The potential at point P is
View SolutionA system of three charges are placed as shown in the figure :
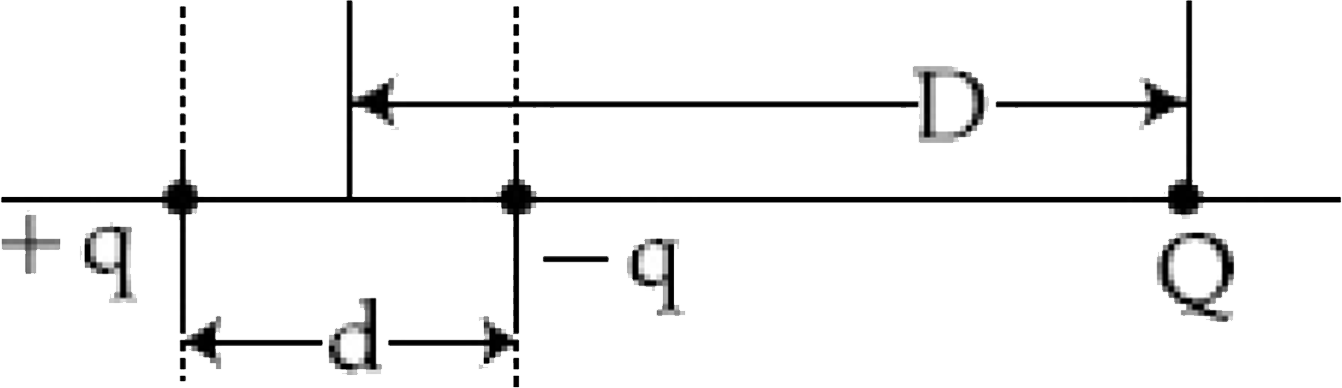
If D>>d, the potential energy of the system is best given by :
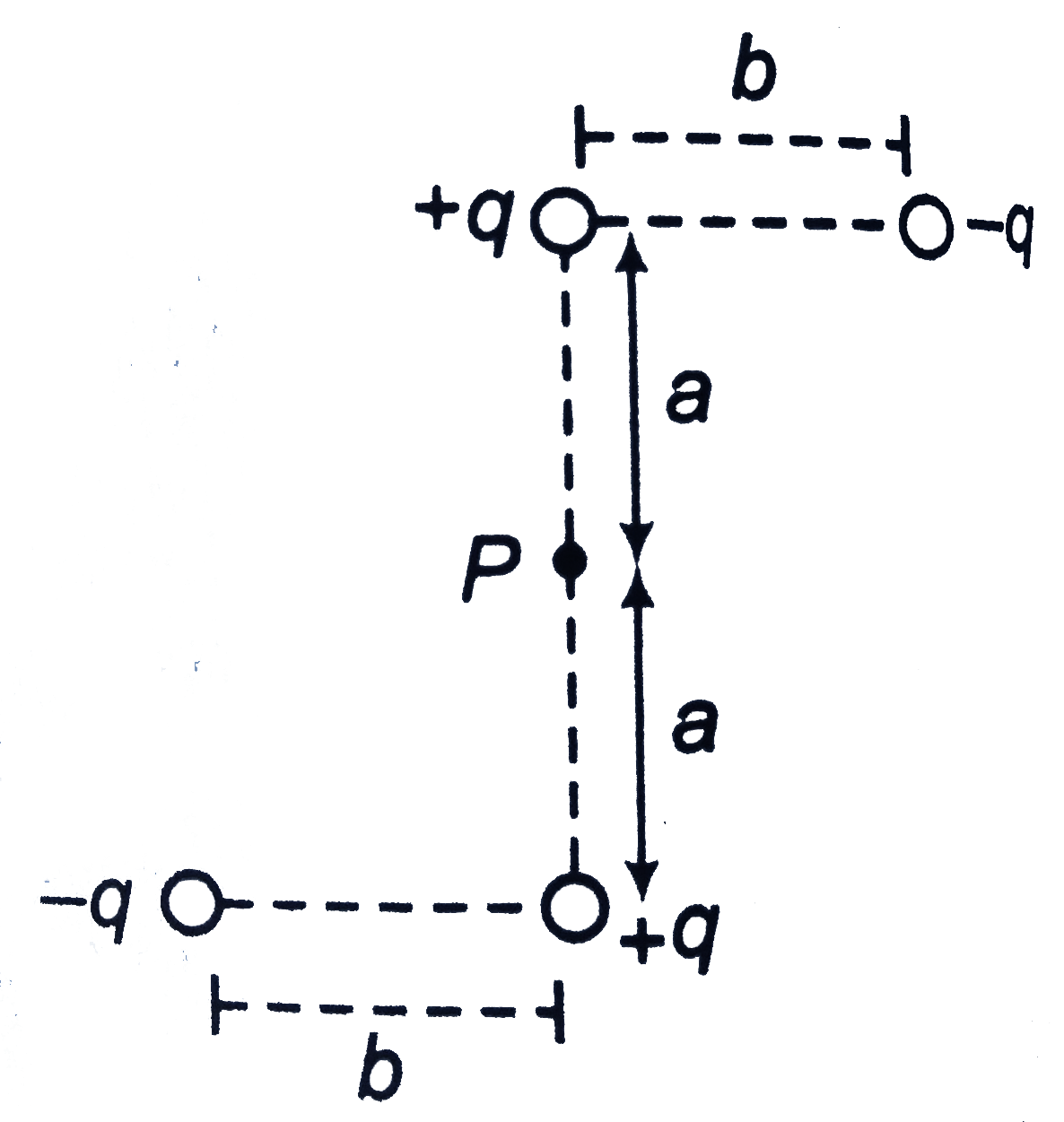
View SolutionThe electrostatic potential due to the charge configuration at point P as shown in figure for b << a is
View SolutionAn infinitely large layer of charge of uniform thickness t is placed normal to an existing uniform electric field. The charge on the sheet alters the electric field so that it still remains uniform on both the sides of the sheet and assumes values E1andE2 as shown in figure. The charge distribution in the layer is not uniform and depends only on the distance from its faces. Find the expressions for the force F per unit experienced by the charge layer.

View SolutionDerive an expression for potential energy of a system of two charges in the absence of the external electrical field.
View Solution

