Among the two interfering monochromatic sources A and B, A is ahead of B in phase by 66∘. If the observation be taken from point P, such that PB−PA=λ/4. Then the phase difference between the waves from A and B reaching P is
156∘
140∘
136∘
126∘
To solve the problem, we need to find the total phase difference between the waves from sources A and B at point P. The total phase difference is the sum of the initial phase difference and the phase difference due to the path difference.
1. Identify the Initial Phase Difference:
- The problem states that source A is ahead of source B by 66∘. Therefore, the initial phase difference (Δϕ0) is:
Δϕ0=66∘
2. Determine the Path Difference:
- We are given that the path difference PB−PA is equal to λ4.
3. Calculate the Phase Difference Due to Path Difference:
- The phase difference (Δϕp) due to the path difference can be calculated using the formula:
Δϕp=360∘λ⋅Δx
- Here, Δx=λ4. Substituting this value in:
Δϕp=360∘λ⋅λ4=360∘4=90∘
4. Calculate the Total Phase Difference:
- The total phase difference (Δϕ) is the sum of the initial phase difference and the phase difference due to the path:
Δϕ=Δϕ0+Δϕp=66∘+90∘=156∘
5. Conclusion:
- The phase difference between the waves from A and B reaching point P is:
Δϕ=156∘
Final Answer:
The phase difference between the waves from A and B reaching point P is 156∘.
---
- The problem states that source A is ahead of source B by 66∘. Therefore, the initial phase difference (Δϕ0) is:
Δϕ0=66∘
- We are given that the path difference PB−PA is equal to λ4.
- The phase difference (Δϕp) due to the path difference can be calculated using the formula:
Δϕp=360∘λ⋅Δx
- Here, Δx=λ4. Substituting this value in:
Δϕp=360∘λ⋅λ4=360∘4=90∘
- The total phase difference (Δϕ) is the sum of the initial phase difference and the phase difference due to the path:
Δϕ=Δϕ0+Δϕp=66∘+90∘=156∘
- The phase difference between the waves from A and B reaching point P is:
Δϕ=156∘
The phase difference between the waves from A and B reaching point P is 156∘.
Similar Questions
Among two interfering sources, let S1 be ahead of the phase by 90∘ relative to S2 . If an observation point P is such that PS1−PS2=1.5λ , the phase difference between the waves from S1andS2 reaching P is
View SolutionIn electromagnetic wave, the phase difference between electric and magnetic field vectors E and B is
View SolutionTwo point sound sources A and B each to power 25πw and frequency 850Hz are 1m apart. The sources are in phase
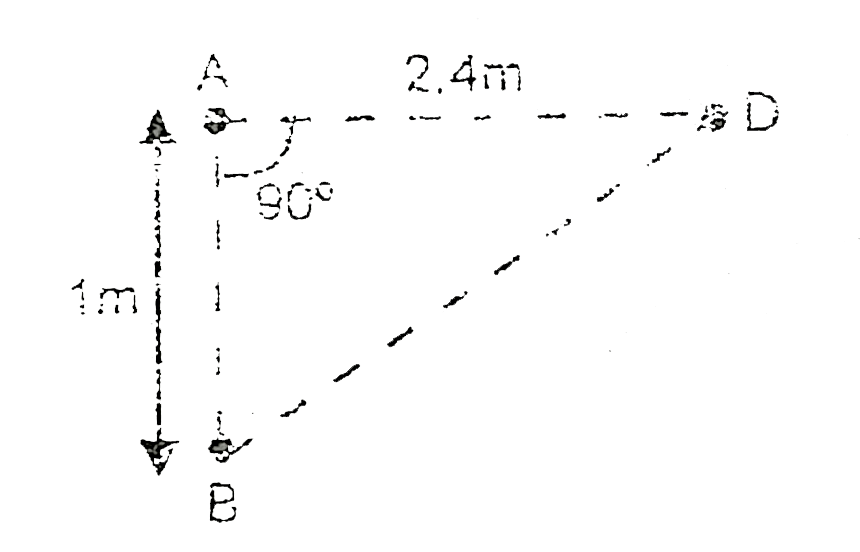
Determine the phase difference between the waves emitting from A and B received by detector D as shown in figure. Velocity of sound =340m/s.View SolutionFigure shows a siphon. The liquid shown in water. The pressure difference PB−PA between the points A and B is
 View Solution
View SolutionIt is found that what waves of same intensity from two coherent sources superpose at a certain point, then the resultant intensity is equal to the intensity of one wave only. This means that the phase difference between the two waves at that point is
View SolutionTwo SHM's are represented by y=asin(ωt−kx) and y=bcos(ωt−kx). The phase difference between the two is :
View SolutionLight waves of wave length λ propagate in a medium. If M end N are two points on the wave front and they are separated by a distance λ/4, the phase difference between them will be (in radian)
View SolutionTwo point sources of sound are kept at a separation of 10 cm. They vibrate in phase to produce waves of wavelength 5.0 cm. What would be the phase difference between the two waves arriving at a point 20 cm from one source (a) on the line joining the sources and (b) on the perpendicular bisector of the line joining the sources ?
View SolutionIn Young's double slit experiment, The locus of the point P lying in a plane with a constant path difference between two interfering waves is
View SolutionTwo points are located at a distance of 10m and 15m from the source of oscillation. The period of oscillation is 0.05s and the velocity of the wave is 300m/s. What is the phase difference between the oscillation of two points?
View Solution

