The equation x2+nx+m=0,n,m∈I can not have
integral roots
non-integral rational roots
irrational roots
complex roots
The correct Answer is:B
To solve the problem, we need to analyze the quadratic equation given as x2+nx+m=0 where n and m are integers. We want to determine which type of roots this equation cannot have.
1. Identify the standard form of the quadratic equation:
The standard form of a quadratic equation is ax2+bx+c=0. In our case, we have:
a=1,b=n,c=m
2. Use the quadratic formula to find the roots:
The roots of the quadratic equation are given by:
x=−b±√b2−4ac2a
Substituting a, b, and c into the formula, we get:
x=−n±√n2−4m2
3. Analyze the discriminant:
The term under the square root, n2−4m, is called the discriminant. We will analyze its value to determine the nature of the roots:
- If n2−4m>0: The roots are real and distinct.
- If n2−4m=0: The roots are real and equal (integral roots).
- If n2−4m<0: The roots are complex.
4. Check the conditions for integral, non-integral, irrational, and complex roots:
- Integral roots: Occur when n2−4m is a perfect square.
- Non-integral roots: Occur when n2−4m is positive but not a perfect square.
- Irrational roots: Occur when n2−4m is positive and not a perfect square.
- Complex roots: Occur when n2−4m<0.
5. Determine which type of roots cannot occur:
- Since n and m are integers, if n2−4m<0, the roots will be complex.
- If n2−4m=0, the roots will be integral.
- If n2−4m>0, we can have both integral and non-integral (including irrational) roots depending on whether n2−4m is a perfect square.
6. Conclusion:
The equation x2+nx+m=0 cannot have complex roots when n and m are integers, as it can have integral, non-integral, and irrational roots depending on the discriminant.
Final Answer:
The equation x2+nx+m=0 cannot have complex roots.
The standard form of a quadratic equation is ax2+bx+c=0. In our case, we have:
a=1,b=n,c=m
The roots of the quadratic equation are given by:
x=−b±√b2−4ac2a
Substituting a, b, and c into the formula, we get:
x=−n±√n2−4m2
The term under the square root, n2−4m, is called the discriminant. We will analyze its value to determine the nature of the roots:
- If n2−4m>0: The roots are real and distinct.
- If n2−4m=0: The roots are real and equal (integral roots).
- If n2−4m<0: The roots are complex.
- Integral roots: Occur when n2−4m is a perfect square.
- Non-integral roots: Occur when n2−4m is positive but not a perfect square.
- Irrational roots: Occur when n2−4m is positive and not a perfect square.
- Complex roots: Occur when n2−4m<0.
- Since n and m are integers, if n2−4m<0, the roots will be complex.
- If n2−4m=0, the roots will be integral.
- If n2−4m>0, we can have both integral and non-integral (including irrational) roots depending on whether n2−4m is a perfect square.
The equation x2+nx+m=0 cannot have complex roots when n and m are integers, as it can have integral, non-integral, and irrational roots depending on the discriminant.
The equation x2+nx+m=0 cannot have complex roots.
Similar Questions
Knowledge Check
If x=2 and x= 3 are the roots of the equation 3x2−2mx+2n=0, then the values of m, n respectively are:
A152,9B15, 7C9, 15D7, 13When the value of n = 2, m can have
A1 valueB3 valuesC4 valuesD7 values.
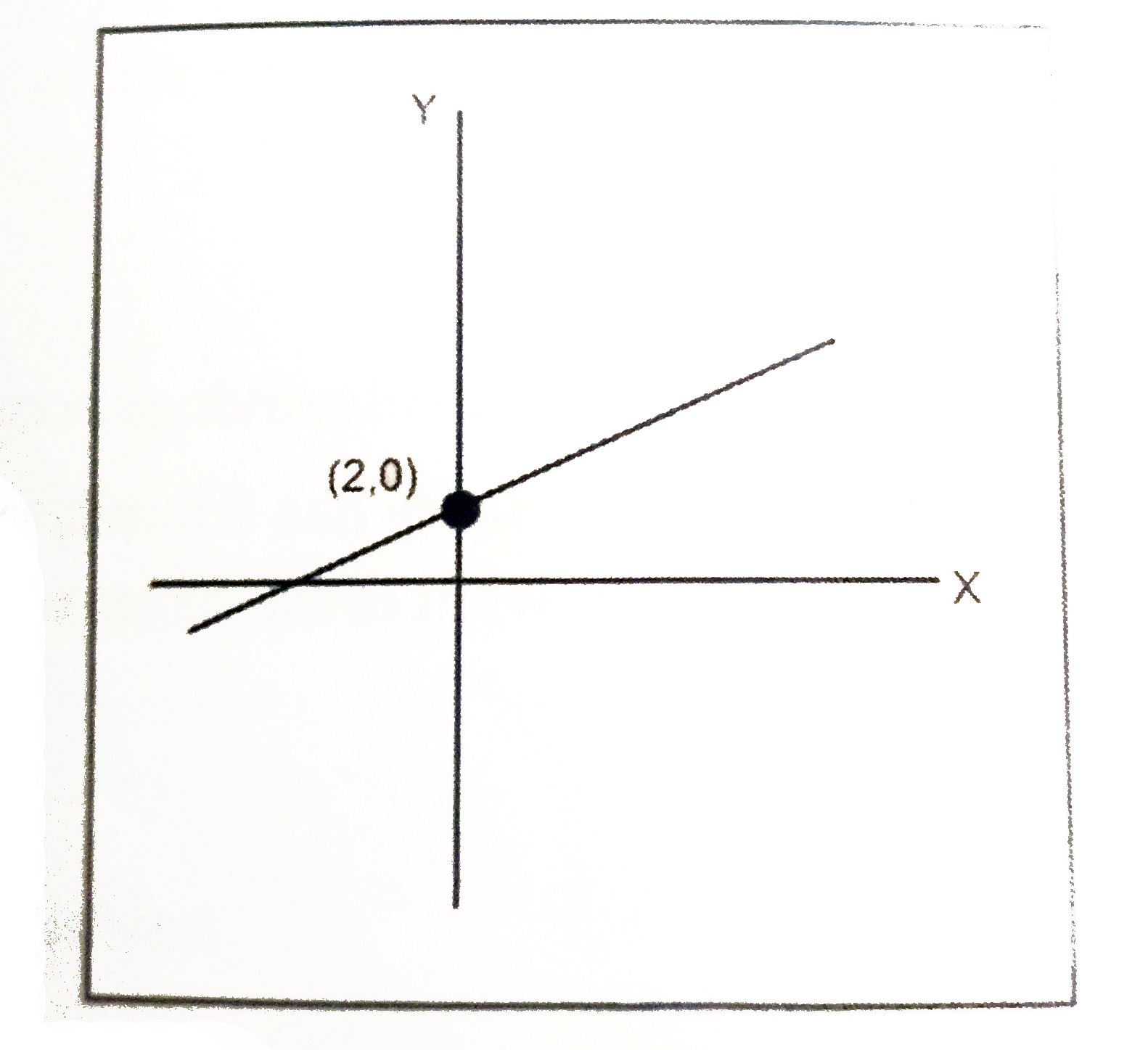
The graph above depicts a straight line having the equation y=mx+n . What can be said about the line given by the equation y=nx+m ?
View SolutionIf the equation x2−(2+m)x+(m2−4m+4)=0 has coincident roots, then
View SolutionIf m be the number of integral solutions of equation 2x2−3xy–9y2−11=0 and n be the roots of x3−[x]−3=0, then m
View SolutionIf x=2 and x=3 are roots of the equation 3x2−mx+2n=0, then find the values of m and m.
View SolutionIf x=2 and x=3 are roots of the equation 3x2−2mx+2n=0, find the values of m and n.
View SolutionThe quadratic equation x2+mx+n=0 has roots which are twice those of x2+px+m=0adm,nandp≠0. The n the value of n/p is _____.
View Solution
