If both the critical points of f(x)=ax3+bx2+cx+d are -ve then
bc>0
bc<0
ab<0
none of these
The correct Answer is:D
To solve the problem, we need to analyze the function f(x)=ax3+bx2+cx+d and its critical points. The critical points are found by setting the first derivative equal to zero.
1. Find the First Derivative:
We start by differentiating the function f(x):
f′(x)=ddx(ax3+bx2+cx+d)=3ax2+2bx+c
2. Set the First Derivative to Zero:
To find the critical points, we set the first derivative equal to zero:
3ax2+2bx+c=0
This is a quadratic equation in the form Ax2+Bx+C=0, where A=3a, B=2b, and C=c.
3. Identify the Roots:
The roots of the quadratic equation can be found using the quadratic formula:
x=−B±√B2−4AC2A=−2b±√(2b)2−4(3a)(c)2(3a)
Simplifying this gives:
x=−2b±√4b2−12ac6a
4. Condition for Critical Points:
We are given that both critical points are negative. This implies:
- The discriminant 4b2−12ac must be non-negative for real roots.
- The sum of the roots (given by −BA=−2b3a) must be negative, which leads to:
−2b3a<0⟹ba>0
This means b and a must have the same sign.
5. Analyzing the Product of Roots:
The product of the roots (given by CA=c3a) must also be positive for both roots to be negative:
c3a>0⟹c and a must have the same sign.
6. Conclusion:
From the above analysis, we can conclude:
- a and b must have the same sign.
- a and c must have the same sign.
- Therefore, a, b, and c must all be either positive or negative together.
We start by differentiating the function f(x):
f′(x)=ddx(ax3+bx2+cx+d)=3ax2+2bx+c
To find the critical points, we set the first derivative equal to zero:
3ax2+2bx+c=0
This is a quadratic equation in the form Ax2+Bx+C=0, where A=3a, B=2b, and C=c.
The roots of the quadratic equation can be found using the quadratic formula:
x=−B±√B2−4AC2A=−2b±√(2b)2−4(3a)(c)2(3a)
Simplifying this gives:
x=−2b±√4b2−12ac6a
We are given that both critical points are negative. This implies:
- The discriminant 4b2−12ac must be non-negative for real roots.
- The sum of the roots (given by −BA=−2b3a) must be negative, which leads to:
−2b3a<0⟹ba>0
This means b and a must have the same sign.
The product of the roots (given by CA=c3a) must also be positive for both roots to be negative:
c3a>0⟹c and a must have the same sign.
From the above analysis, we can conclude:
- a and b must have the same sign.
- a and c must have the same sign.
- Therefore, a, b, and c must all be either positive or negative together.
Similar Questions
Knowledge Check
If in the quadratic function f(x)=ax2+bx+c, a and c are both negative constant, which of the following could be the graph of function f?
A B
B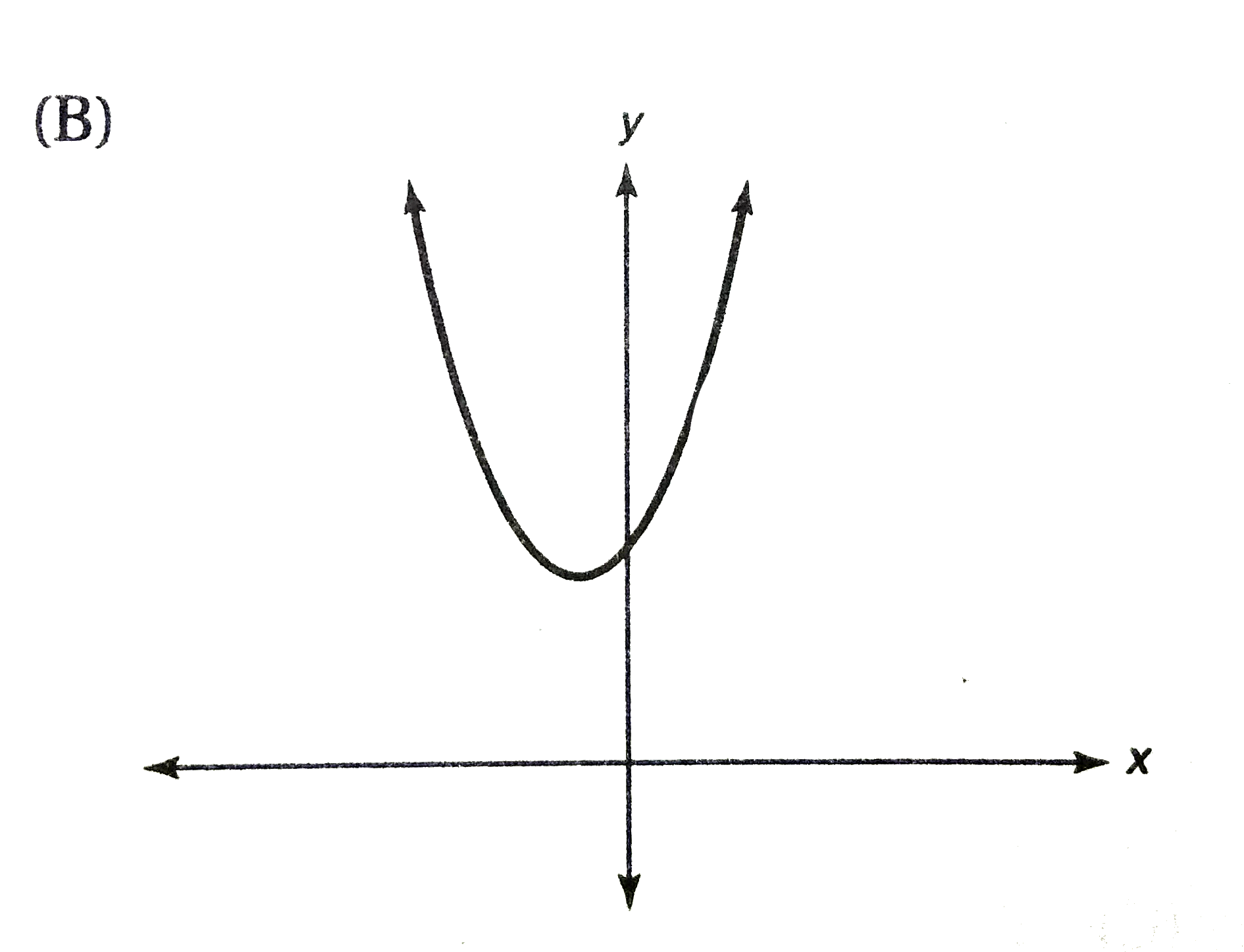 C
C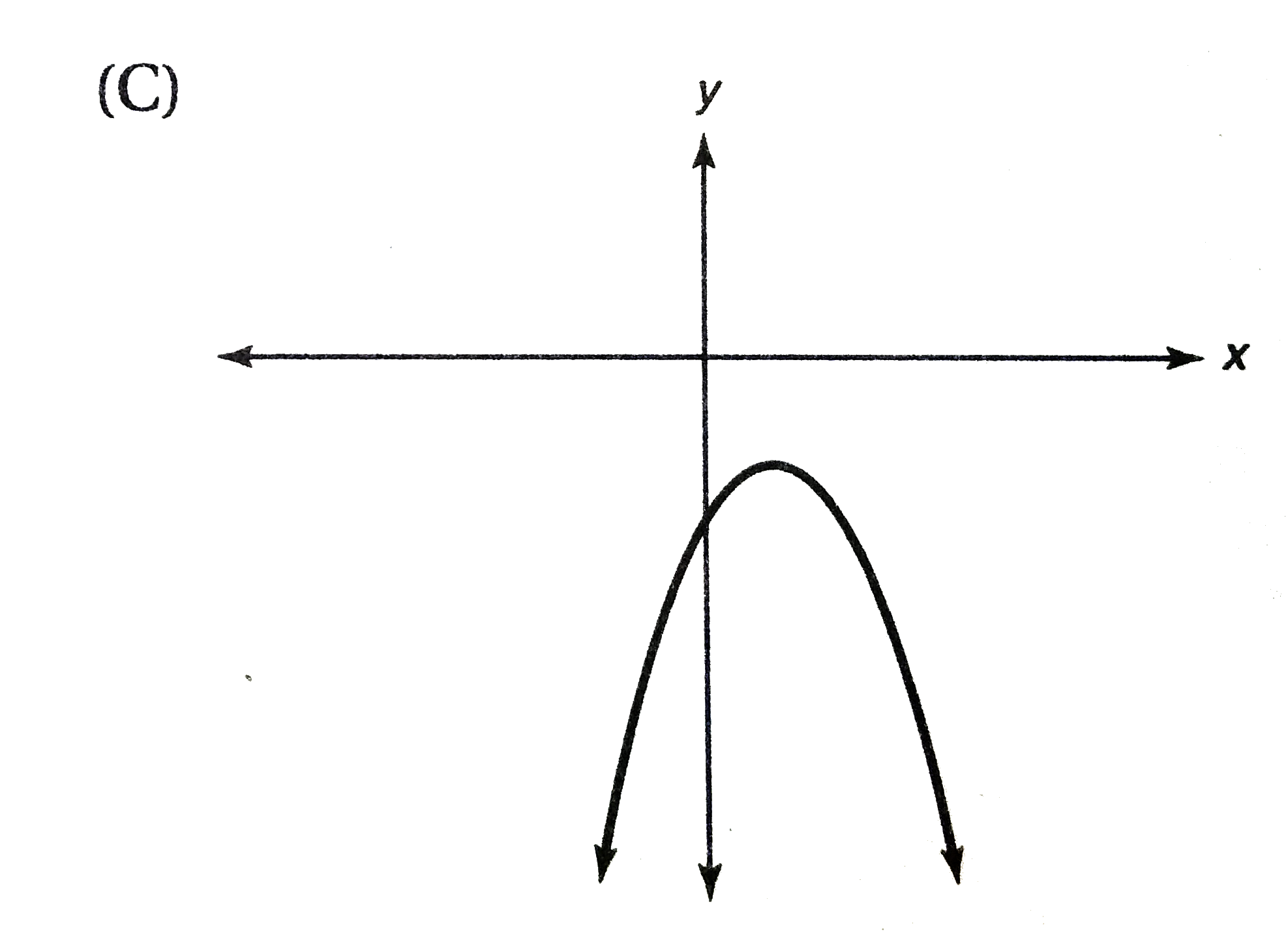 D
D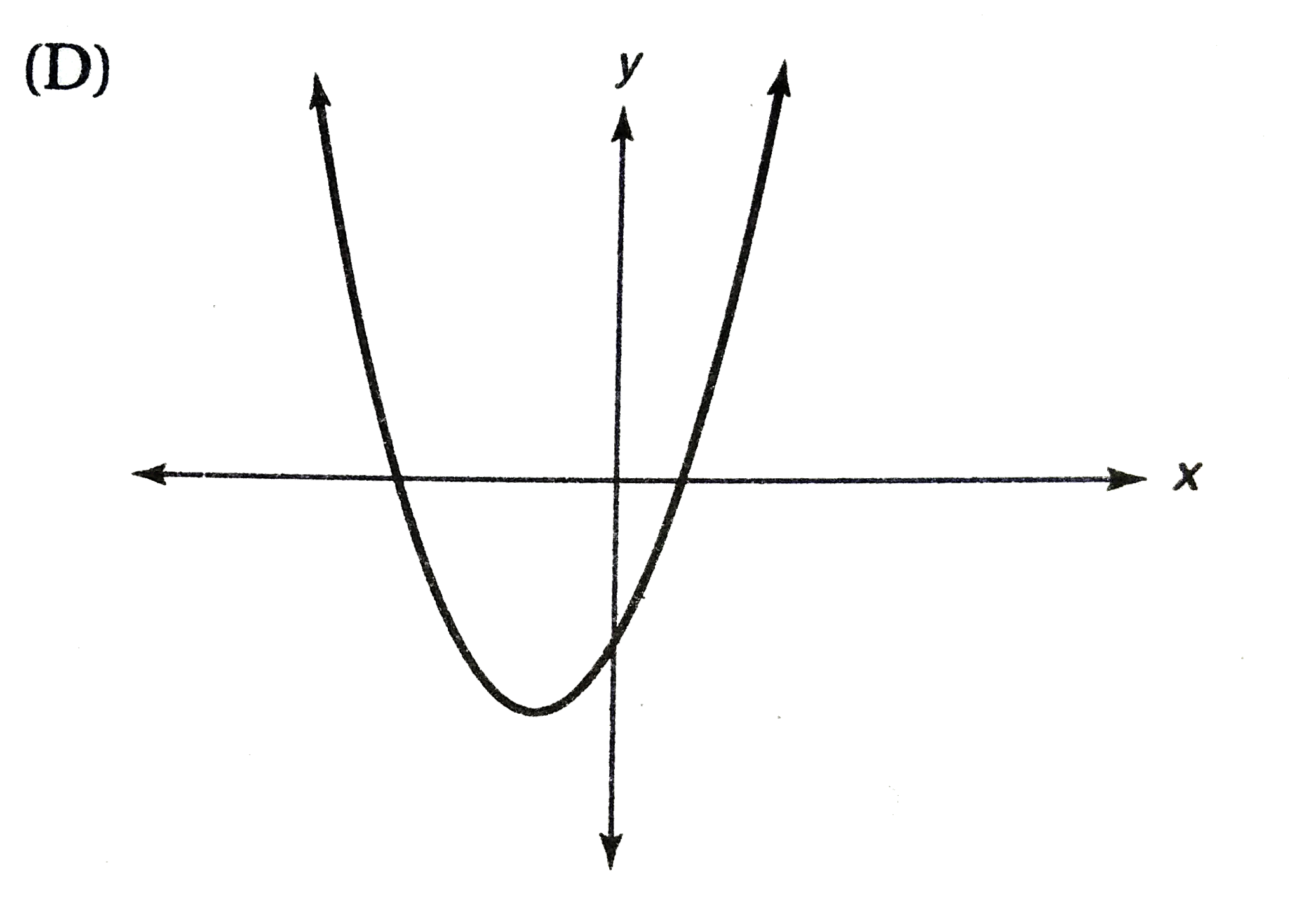
If the roots of the equation x3+bx2+cx+d=0 are in arithmetic progression, then b, c and d satisfy the relation
View SolutionIf 1, -2, 3 are the roots of ax3+bx2+cx+d=0 then the roots of ax3+3bx2+9cx+27d=0 are
View SolutionIf the roots of ax3+bx2+cx+d=0 are in G.P then the roots of dx3−cx2+bx−a=0 are in
View SolutionThe roots of the equation x5−40x4+ax3+bx2+cx+d=0 are in GP. Lf sum of reciprocals of the roots is 10, then find |c|and|d|
View SolutionIf the cubic polymomial y=ax3+bx2+cx+d(a,b,c,d∈R) has only one critical point in its entire domain and ac=2, then the value of |b| is:
View SolutionIf f(x)=x3+bx2+cx+d and 0<b2<c, then
View SolutionIf one of the zeroes of the cubic polynomial ax3+bx2+cx+d is zero, the product of the other two zeroes is :
View Solution
