If 4sin2x−8sinx+3≤0,0≤x≤2π then the solution set for x is
(0,π)
(0,π4)
(π4,π)
(π6,5π6)
The correct Answer is:d
To solve the inequality 4sin2x−8sinx+3≤0 for 0≤x≤2π, we will follow these steps:
Step 1: Rewrite the inequality
We start with the given inequality:
4sin2x−8sinx+3≤0
Step 2: Factor the quadratic expression
This is a quadratic inequality in terms of sinx. We can factor it:
4sin2x−8sinx+3=(2sinx−3)(2sinx−1)
Thus, we rewrite the inequality as:
(2sinx−3)(2sinx−1)≤0
Step 3: Find the critical points
To find the critical points, we set each factor to zero:
1. 2sinx−3=0⇒sinx=32 (not possible since sinx cannot exceed 1)
2. 2sinx−1=0⇒sinx=12
The only valid critical point is sinx=12.
Step 4: Determine the intervals
Next, we analyze the sign of the product (2sinx−3)(2sinx−1) in the intervals determined by the critical points. The relevant intervals are:
- (−∞,12)
- (12,∞)
Step 5: Test intervals
1. For sinx<12 (e.g., sinx=0):
(2⋅0−3)(2⋅0−1)=(−3)(−1)>0 (positive)
2. For sinx=12:
(2⋅12−3)(2⋅12−1)=(1−3)(1−1)=(−2)(0)=0 (zero)
3. For sinx>12 (e.g., sinx=1):
(2⋅1−3)(2⋅1−1)=(2−3)(2−1)=(−1)(1)<0 (negative)
Step 6: Combine the results
The inequality (2sinx−3)(2sinx−1)≤0 holds in the interval:
12≤sinx≤1
Step 7: Find the angles corresponding to sinx=12 and sinx=1
- sinx=12 gives x=π6,5π6
- sinx=1 gives x=π2
Step 8: Write the solution set
Thus, the solution set for x in the interval 0≤x≤2π is:
x∈(π6,5π6)∪(π2,π2)
Final Solution
The final solution set for x is:
(π6,5π6)
We start with the given inequality:
4sin2x−8sinx+3≤0
This is a quadratic inequality in terms of sinx. We can factor it:
4sin2x−8sinx+3=(2sinx−3)(2sinx−1)
Thus, we rewrite the inequality as:
(2sinx−3)(2sinx−1)≤0
To find the critical points, we set each factor to zero:
1. 2sinx−3=0⇒sinx=32 (not possible since sinx cannot exceed 1)
2. 2sinx−1=0⇒sinx=12
Next, we analyze the sign of the product (2sinx−3)(2sinx−1) in the intervals determined by the critical points. The relevant intervals are:
- (−∞,12)
- (12,∞)
1. For sinx<12 (e.g., sinx=0):
(2⋅0−3)(2⋅0−1)=(−3)(−1)>0 (positive)
2. For sinx=12:
(2⋅12−3)(2⋅12−1)=(1−3)(1−1)=(−2)(0)=0 (zero)
(2⋅1−3)(2⋅1−1)=(2−3)(2−1)=(−1)(1)<0 (negative)
The inequality (2sinx−3)(2sinx−1)≤0 holds in the interval:
12≤sinx≤1
- sinx=12 gives x=π6,5π6
- sinx=1 gives x=π2
Thus, the solution set for x in the interval 0≤x≤2π is:
x∈(π6,5π6)∪(π2,π2)
The final solution set for x is:
(π6,5π6)
Similar Questions
Knowledge Check
If 2x−3≤x+1≤4x+7,x∈I (integers), then the solution set of x is
A{−2,−1,0,1,2,3,4}B{−1,0,1,2,3}C{−2,−1,0,1,2,3}D{−1,0,1,2,3,4}If 2≤2x−3≤5,x∈I, then the solution set of x on the number line is:
A B
B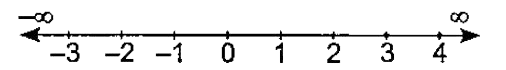 C
C D
D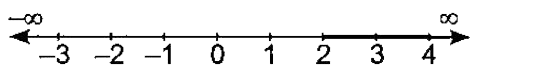
If 2x−5≤5x+4≤11 and x is a natural number (N), then the solution set of x is
A{1}B{−3,−2,−1,0,1}C{−2,−1,0,1}D{−2,−1,0}
If 2sinx−1≤0and x∈[0,2π], then the solution set for x, is
View SolutionIf cosx=√1−sin2x,0≤x≤π then a value of x is
View SolutionIf sin4x+cos4y+2=4sinx.cosy and 0≤x,y≤π2 then sin x + cos y is equal to
View SolutionIf a.3tanx+a.3−tanx−2=0 has real solutions, x≠π2,0≤x≤π, then find the set of all possible values of parameter 'a'.
View SolutionThe equation sinx+siny+sinz=−3 for 0≤x≤2π, 0≤y≤2π,o≤z≤2π, has
View Solution
