An electric dipole is placed at the centre of a sphere. Select the correct alternative(s).
The flux of electric field through the sphere is zero
The electric field is zero at every point of the sphere
The electric field is not zero anywhere on the sphere
The electric field is zero on a circle on the sphere
The correct Answer is:A, C
To solve the problem regarding the electric dipole placed at the center of a sphere, we can follow these steps:
Step 1: Understand the Electric Dipole
An electric dipole consists of two equal and opposite charges separated by a distance. For example, we can represent it as +q and -q.
Step 2: Apply Gauss's Law
According to Gauss's Law, the electric flux (Φ) through a closed surface is given by the equation:
Φ=Qencϵ0
where Qenc is the total charge enclosed by the surface and ϵ0 is the permittivity of free space.
Step 3: Determine the Charge Enclosed
In our case, the dipole consists of two charges (+q and -q). When we consider a sphere centered at the dipole, the total charge enclosed by the sphere is:
Qenc=+q+(−q)=0
Step 4: Calculate the Electric Flux
Since the total charge enclosed by the sphere is zero, we can substitute this into Gauss's Law:
Φ=0ϵ0=0
Thus, the electric flux through the sphere is zero.
Step 5: Analyze the Electric Field Inside the Sphere
The electric field (E) due to an electric dipole at a point in space can be expressed as:
E=K⋅pr3⋅(3cos2θ−1)
where K is a constant, p is the dipole moment, r is the distance from the dipole, and θ is the angle between the dipole axis and the line connecting the dipole to the point of interest.
Step 6: Evaluate the Electric Field at Points on the Sphere
For any point on the surface of the sphere, the electric field will not be zero. The expression for the electric field indicates that it depends on the angle θ, and since cos2θ is always greater than or equal to zero, the electric field will always have a non-zero value at any point on the sphere.
Conclusion
From the analysis, we can conclude:
1. The electric flux through the sphere is zero (due to the enclosed charge being zero).
2. The electric field is not zero at any point on the surface of the sphere.
Correct Alternatives
Thus, the correct alternatives based on the analysis are:
- The flux of electric field through the sphere is zero.
- The electric field is not zero at every point of the sphere.
An electric dipole consists of two equal and opposite charges separated by a distance. For example, we can represent it as +q and -q.
According to Gauss's Law, the electric flux (Φ) through a closed surface is given by the equation:
Φ=Qencϵ0
where Qenc is the total charge enclosed by the surface and ϵ0 is the permittivity of free space.
In our case, the dipole consists of two charges (+q and -q). When we consider a sphere centered at the dipole, the total charge enclosed by the sphere is:
Qenc=+q+(−q)=0
Since the total charge enclosed by the sphere is zero, we can substitute this into Gauss's Law:
Φ=0ϵ0=0
Thus, the electric flux through the sphere is zero.
The electric field (E) due to an electric dipole at a point in space can be expressed as:
E=K⋅pr3⋅(3cos2θ−1)
where K is a constant, p is the dipole moment, r is the distance from the dipole, and θ is the angle between the dipole axis and the line connecting the dipole to the point of interest.
For any point on the surface of the sphere, the electric field will not be zero. The expression for the electric field indicates that it depends on the angle θ, and since cos2θ is always greater than or equal to zero, the electric field will always have a non-zero value at any point on the sphere.
From the analysis, we can conclude:
1. The electric flux through the sphere is zero (due to the enclosed charge being zero).
2. The electric field is not zero at any point on the surface of the sphere.
Thus, the correct alternatives based on the analysis are:
- The flux of electric field through the sphere is zero.
- The electric field is not zero at every point of the sphere.
Similar Questions
Knowledge Check
An electric dipole is placed at the centre of a sphere. Mark the correct options:
AElectric field is zero at every point of the sphereBElectic field is zero anywhere on the sphereCThe flux of electric field is not zero through the sphereDAll of these
An electric dipole is placed at the centre of a sphere. Find the electric flux passing through the sphere.
View SolutionAn electric dipole is placed at the centre of a spherical shell. Find the electric field at an external point of the shell.
View SolutionA positively charged disc is placed on a horizontal plane. A charged particle is released from a certain height on its axis. The particle just reaches the centre of the disc. Select the correct alternative.
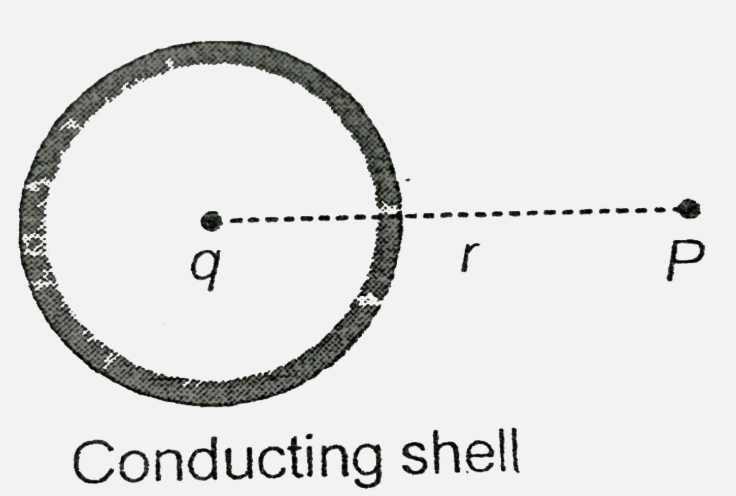
View SolutionFigure shows a point charge q, placed at the centre of a hollow conducting shell and a point P , outside the shell. The distance between centre and point P is r. Select the correct alternative (s).
View SolutionAn electric dipole is placed in uniform electric field as shown in the figure. The dipole is slightly rotated about its centre and released. Select the correct statement(s).
View SolutionA short electric dipoleis placed along y-axis at the origin. The electric field vector at a point P on x-axis is →E1. The dipole is rotated by π2 at its positin . Now, the electric field vector at point P is →E2. Select the correct alternative(s) :
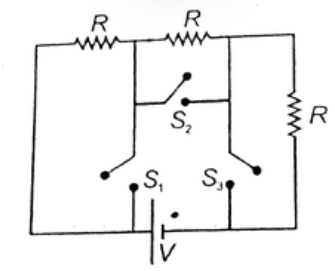
View SolutionIf all the resistors are identical , select the correct alternative (s).
View Solution
