Three infinitely charged sheets are kept parallel to x - y plane having charge densities as shown. Then the value of electric field at 'P' is
A. −4σ∈0ˆk
B. 4σ∈0ˆk
C. −2σ∈0ˆk
D. 2σ∈0ˆk
−4σ∈0ˆk
4σ∈0ˆk
−2σ∈0ˆk
2σ∈0ˆk
The correct Answer is:C
To find the electric field at point P due to three infinitely charged sheets with given charge densities, we can follow these steps:
1. Identify Charge Densities:
- Let the charge densities of the three sheets be:
- Sheet 1: σ (positive)
- Sheet 2: −2σ (negative)
- Sheet 3: −σ (negative)
2. Determine Electric Field from Each Sheet:
- The electric field E due to an infinite sheet with surface charge density σ is given by:
E=σ2ϵ0
- The direction of the electric field due to a positively charged sheet is away from the sheet, while for a negatively charged sheet, it is towards the sheet.
3. Calculate Electric Field Contributions:
- From Sheet 1 (charge density σ):
- E1=σ2ϵ0 (away from the sheet, in the positive z-direction)
- From Sheet 2 (charge density −2σ):
- E2=−−2σ2ϵ0=2σ2ϵ0=σϵ0 (towards the sheet, in the negative z-direction)
- From Sheet 3 (charge density −σ):
- E3=−−σ2ϵ0=σ2ϵ0 (towards the sheet, in the negative z-direction)
4. Determine the Net Electric Field:
- The net electric field Enet at point P is the vector sum of the electric fields from all three sheets:
Enet=E1+E2+E3
- Substituting the values:
Enet=σ2ϵ0−2σ2ϵ0−σ2ϵ0
- Simplifying this:
Enet=σ2ϵ0−2σ2ϵ0−σ2ϵ0=σ−2σ−σ2ϵ0=−2σ2ϵ0=−σϵ0
5. Direction of the Electric Field:
- Since the net electric field is negative, it indicates that the direction is in the negative z-direction (i.e., −^k).
6. Final Result:
- Therefore, the electric field at point P is:
Enet=−2σϵ0^k
Conclusion:
The correct answer is option C: −2σϵ0^k.
- Let the charge densities of the three sheets be:
- Sheet 1: σ (positive)
- Sheet 2: −2σ (negative)
- Sheet 3: −σ (negative)
- The electric field E due to an infinite sheet with surface charge density σ is given by:
E=σ2ϵ0
- The direction of the electric field due to a positively charged sheet is away from the sheet, while for a negatively charged sheet, it is towards the sheet.
- From Sheet 1 (charge density σ):
- E1=σ2ϵ0 (away from the sheet, in the positive z-direction)
- From Sheet 2 (charge density −2σ):
- E2=−−2σ2ϵ0=2σ2ϵ0=σϵ0 (towards the sheet, in the negative z-direction)
- From Sheet 3 (charge density −σ):
- E3=−−σ2ϵ0=σ2ϵ0 (towards the sheet, in the negative z-direction)
- The net electric field Enet at point P is the vector sum of the electric fields from all three sheets:
Enet=E1+E2+E3
- Substituting the values:
Enet=σ2ϵ0−2σ2ϵ0−σ2ϵ0
- Simplifying this:
Enet=σ2ϵ0−2σ2ϵ0−σ2ϵ0=σ−2σ−σ2ϵ0=−2σ2ϵ0=−σϵ0
- Since the net electric field is negative, it indicates that the direction is in the negative z-direction (i.e., −^k).
- Therefore, the electric field at point P is:
Enet=−2σϵ0^k
The correct answer is option C: −2σϵ0^k.
Similar Questions
Knowledge Check
Two infinite plane parallel sheets, separated by a distance d have equal and opposite uniform charge densities σ. Electric field at a point between the sheets is
Aσ2ε0Bσε0CzeroDdepends on the location of the point
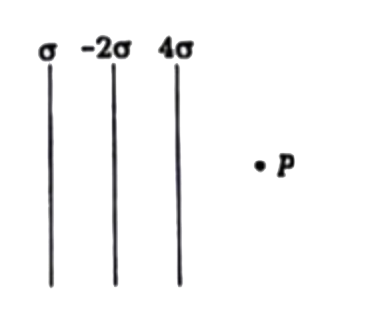
Three non-conducting large parallel plates have surface charge densities σ,−2σand4σ respectively as shown in the figure. The electric field at the point P is
View SolutionIf three infinite charged sheets of uniform surface charge densities σ,2σ and −4σ are placed as shown in figure, then find out electric field intensities at points A, B, C and D.

View SolutionTwo paralle plane sheets 1 and 2 carry uniform charge densites σ1andσ2 (see fig. The electric field in the region marked I is (σ1>σ2):

View SolutionThere are three concentric thin spheres of radius a,b,c(a>b>c). The total surface charge densities on their surfaces are σ,−σ,σ respectively. The magnitude of the electric field at r (distance from centre) such that a>r>b is:
A. 0
B. σε0r2(b2−c2)
C. σε0r(a2+b2)
D. none of these
View SolutionElectric field at the centre of uniformly charge hemispherical shell of surface charge density σ is σnε0 then find the value of n.
View SolutionTwo infinitely large charged planes having uniform suface charge density +σ and −σ are placed along x−y plane and yz plane respectively as shown in the figure. Then the nature of electric lines of forces in x−z plane is given by:

View SolutionThree concentric spherical metallic shells A,B and C of radii a,b and c (a<b<c) have surface charge densities σ,−σandσ respectively.
If the potential of shell B is VB=σ∈0(anb−b+c) and the potential of shell C is VC=σ∈0(anc−bnc+c) then n is .
View Solution