On a particular day , the maximum frequency reflected from the ionosphere is 9MHz. On another day , it was found to increase by 1MHz. Calculate , the ratio of the maximum electron densities of the ionosphere on the two days .
The correct Answer is:0.81
To solve the problem, we need to use the relationship between the maximum frequency reflected from the ionosphere and the maximum electron density. The relationship can be expressed as follows:
f=k√N
Where:
- f is the maximum frequency reflected (in Hz),
- N is the maximum electron density (in electrons per cubic meter),
- k is a constant.
For our calculations, we can ignore the constant k since we are interested in the ratio of electron densities on two different days.
1. Identify the frequencies:
- On the first day, the maximum frequency f1=9MHz.
- On the second day, the maximum frequency f2=9MHz+1MHz=10MHz.
2. Express the electron densities:
- Let the maximum electron density on the first day be N1.
- Let the maximum electron density on the second day be N2.
3. Set up the equations using the relationship:
- From the relationship f=k√N, we can write:
f1=k√N1⟹N1=(f1k)2
f2=k√N2⟹N2=(f2k)2
4. Calculate the ratio of the electron densities:
- The ratio of the maximum electron densities can be expressed as:
N2N1=(f2k)2(f1k)2=(f2f1)2
5. Substitute the frequencies:
- Substitute f1=9MHz and f2=10MHz:
N2N1=(109)2
6. Calculate the numerical value:
- Now calculate (109)2:
N2N1=(109)2=10081≈1.2346
7. Final ratio:
- The ratio of the maximum electron densities N2:N1=100:81.
Final Answer:
The ratio of the maximum electron densities of the ionosphere on the two days is 10081 or approximately 1.2346.
- f is the maximum frequency reflected (in Hz),
- N is the maximum electron density (in electrons per cubic meter),
- k is a constant.
- On the first day, the maximum frequency f1=9MHz.
- On the second day, the maximum frequency f2=9MHz+1MHz=10MHz.
- Let the maximum electron density on the first day be N1.
- Let the maximum electron density on the second day be N2.
- From the relationship f=k√N, we can write:
f1=k√N1⟹N1=(f1k)2
f2=k√N2⟹N2=(f2k)2
- The ratio of the maximum electron densities can be expressed as:
N2N1=(f2k)2(f1k)2=(f2f1)2
- Substitute f1=9MHz and f2=10MHz:
N2N1=(109)2
- Now calculate (109)2:
N2N1=(109)2=10081≈1.2346
- The ratio of the maximum electron densities N2:N1=100:81.
The ratio of the maximum electron densities of the ionosphere on the two days is 10081 or approximately 1.2346.
Similar Questions
Knowledge Check
On a particular day, the maximum frequency reflected from the ionosphere is 10 MHz. On another day, it was found to increase to 11 MHz. Calculate the ratio of the maximum electron densities of the ionosphere on the two days. Point out a plausible explanation for this.
A1.21B0.82C0.50D0.25On a particular day, the maximum frequency reflected from the ionosphere is 10 MHz. On another day, it was found to increase to 11 MHz. Calculate the ratio of the maximum electron densities of the ionosphere on the two days. Point out a plausible explanation for this.
A1.21B0.82C0.50D0.25
Two waves of equal frequencies have their amplitude in the ratio of 5:3. They are superimposed on each other. Calculate the ratio of the maximum to minimum intensities of the resultant wave.
View SolutionThe maximum fequency for reflection of sky waves from a certain layer of the ionosphere is found to be fmax=9(Nmax)1/2, Where N _max is the maximum electron density at that layer of the ionosphere.On a certain day it is observed that signals of frequencies higher than 5 MHz are not received by reflection from the F1 layer of the ionosphere while signals of frequencies higher than 8 MHz are not received by reflection from the F2 layer of the ionosphere. Estimate the maximum electron densities of the F1 and F2 layers on that day.
View SolutionTwo waves of equal frequencies have their amplitudes in the
ratio of 3:5. They are superimposed on each other. Calculate the ratio of
maximum and minimum intensities of the resultant wave.
View SolutionA metallic surface is illuminated alternatively with light of wavelenghts 3000Å and 6000Å. It is observed that the maximum speeds of the photoelectrons under these illuminations are in the ratio 3 : 1 . Calculate the work function of the metal and the maximum speed of the photoelectrons in two cases.
View SolutionA point sources S emitting light of wavelength 600nm is placed at a very small height h above the flat reflecting surface AB(see figure).The intensity of the reflected light is36% of the intensity.interference firnges are observed on a screen placed parallel to the reflecting surface a very large distance D from it.
(A)What is the shape of the interference fringes on the screen?
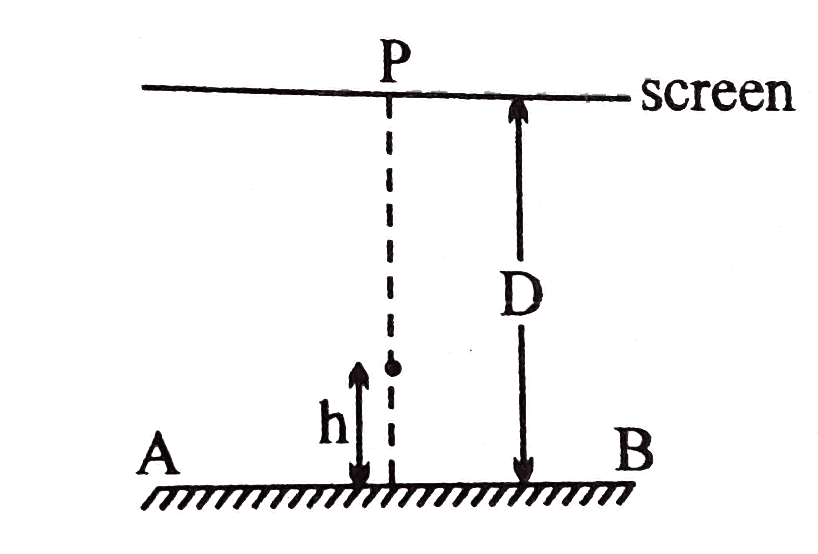
(B)Calculate the ratio of the minimum to the maximum to the maximum intensities in the interference fringes fromed near the point P (shown in the figure) (c) if the intenstities at point P corresponds to a maximum,calculate the minimum distance through which the reflecting surface AB should be shifted so that the intensity at P again becomes maximum.
View SolutionIn a class, the total numbers of boys and girls are in the ratio 4 : 3. On one day it was found that 8 boys and 14 girls were absent from the class and that the number of boys was the square of the number of girls. What is the total number of students in the class ?
View Solution
