Let an=827nn! for n∈N , then an is greatest when
n=824
n=825
n = 826
n = 828
The correct Answer is:C
To determine when the sequence an=827nn! is greatest, we can analyze the ratio of consecutive terms, an+1an.
1. Define the terms:
an=827nn!
an+1=827n+1(n+1)!
2. Find the ratio of consecutive terms:
an+1an=827n+1(n+1)!⋅n!827n=827n+1
3. Determine when the sequence is increasing:
The sequence an is increasing when an+1an>1:
827n+1>1
This simplifies to:
827>n+1⇒n<826
4. Determine when the sequence is decreasing:
The sequence an starts to decrease when an+1an<1:
827n+1<1
This simplifies to:
827<n+1⇒n>826
5. Conclusion:
The sequence an increases for n<826 and decreases for n>826. Therefore, the maximum value occurs at n=826.
Thus, the value of n for which an is greatest is:
826
an=827nn!
an+1=827n+1(n+1)!
an+1an=827n+1(n+1)!⋅n!827n=827n+1
The sequence an is increasing when an+1an>1:
827n+1>1
This simplifies to:
827>n+1⇒n<826
The sequence an starts to decrease when an+1an<1:
827n+1<1
This simplifies to:
827<n+1⇒n>826
The sequence an increases for n<826 and decreases for n>826. Therefore, the maximum value occurs at n=826.
826
Similar Questions
Let an=1000nn! for n∈N, then an is greatest, when value of n is
View SolutionLet an=(1+1n)n. Then for each n∈N
View SolutionIf <an>and<bn> be two sequences given by an=(x)12n+(y)12nandbn=(x)12n−(y)12n for all n∈N. Then, a1a2a3.....an is equal to
View SolutionIf a1=1,a2=1,andan=an−1+an−2 for n≥3, find the first 7 terms of the sequence.
View SolutionLet a sequence whose nth term is {an} be defined as
a1=12 and (n−1)an−1=(n+1)an for n≥2 then Limn→∞Sn equals
View SolutionLet an=∫π/20(1−sint)nsin2t,
then limn→∞n∑n=1annis equal to
View SolutionLet a0=0 and an=3an−1+1 for n≥1. Then the remainder obtained dividing a2010 by 11 is
View SolutionThe figure shows a graph between 1n∣∣∣AnA1∣∣∣ and 1n|n|, where An is the area enclosed by the nth orbit in a hydrogen like atom. The correct curve is
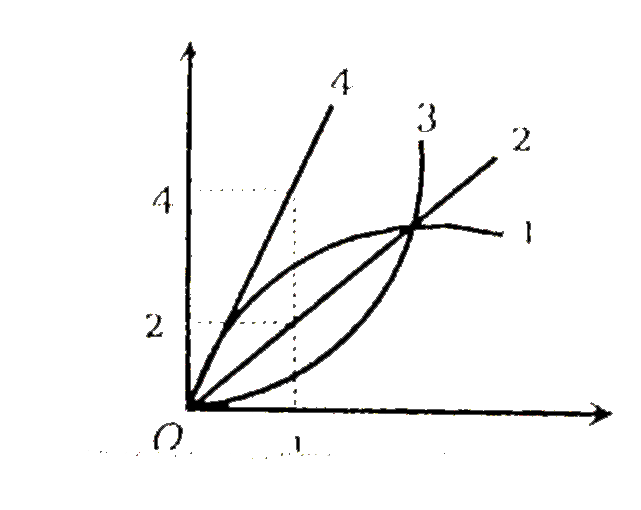
View SolutionThe figure shows a graph between 1n∣∣∣AnA1∣∣∣ and 1n|n|, where An is the area enclosed by the nth orbit in a hydrogen like atom. The correct curve is
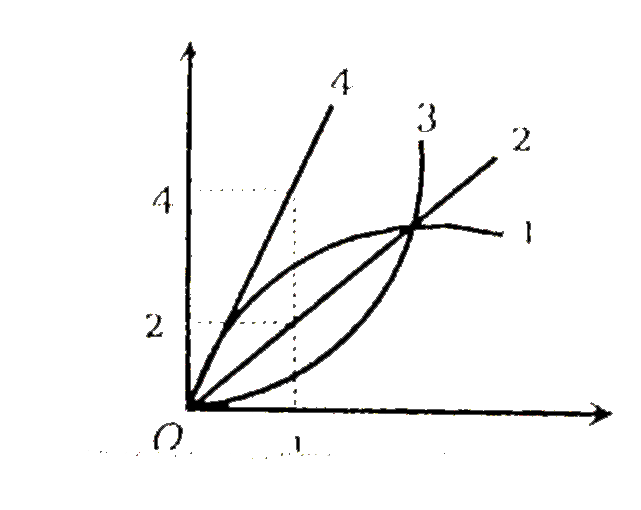
View SolutionIf a1 is the greatest value of f(x) , where f(x)=(12+[sinx]) (where [.] denotes greatest integer function) and an−1=(−1)n−2(n+1)+an (where n in N), then limn→∞(an) is
View Solution
