The speed of water is double that of swimmer's velocity relative to water ?What should be the direction of the swimmer so as to express minimum displacement assuming ?
To solve the problem, we need to determine the direction in which the swimmer should swim to achieve the minimum displacement when the speed of the water is double that of the swimmer's velocity relative to the water.
1. Identify Given Values:
- Let the swimmer's velocity relative to water be vm=5m/s.
- The speed of water vw is double that of the swimmer's velocity relative to water:
vw=2⋅vm=2⋅5m/s=10m/s.
2. Set Up the Relationship:
- We know that the ratio of the swimmer's velocity relative to water and the velocity of water is given as:
vmvw=12.
- This implies that:
sinθ=vmvw=12.
3. Calculate the Angle:
- To find the angle θ, we take the inverse sine:
θ=sin−1(12).
- The value of sin−1(12) is:
θ=30∘.
4. Determine the Direction of the Swimmer:
- The swimmer must swim at an angle θ with respect to the direction of the water flow. Since the water is flowing in one direction (let's say horizontally), the swimmer will need to swim at an angle of 30∘ upstream.
- To express this direction in relation to the standard coordinate system, we add 90∘ to 30∘ (since we are considering the angle from the positive x-axis):
Direction of swimmer=30∘+90∘=120∘.
5. Final Answer:
- Therefore, the direction in which the swimmer should swim to achieve minimum displacement is:
120 degrees from the positive x-axis.
- Let the swimmer's velocity relative to water be vm=5m/s.
- The speed of water vw is double that of the swimmer's velocity relative to water:
vw=2⋅vm=2⋅5m/s=10m/s.
- We know that the ratio of the swimmer's velocity relative to water and the velocity of water is given as:
vmvw=12.
- This implies that:
sinθ=vmvw=12.
- To find the angle θ, we take the inverse sine:
θ=sin−1(12).
- The value of sin−1(12) is:
θ=30∘.
- The swimmer must swim at an angle θ with respect to the direction of the water flow. Since the water is flowing in one direction (let's say horizontally), the swimmer will need to swim at an angle of 30∘ upstream.
- To express this direction in relation to the standard coordinate system, we add 90∘ to 30∘ (since we are considering the angle from the positive x-axis):
Direction of swimmer=30∘+90∘=120∘.
- Therefore, the direction in which the swimmer should swim to achieve minimum displacement is:
120 degrees from the positive x-axis.
Similar Questions
The stream of a river is flowing with a speed of 2km/h. A swimmer can swim at a speed of 4km/h. What should be the direction of the swimmer with respect to the flow of the river ot cross the river straight ?
View SolutionA man who can swim at a velocity v relative to water wants to cross a river of width b, flowing with a speed u.
View SolutionA man who can swim at a velocity v relative to water wants to cross a river of width b, flowing with a speed u.
View SolutionIf speed of water in river is 4 m/s and speed of swimmer with respect to water is 3 m/s, then in which direction the swimmer must swim so that he will reach directly opposite end?
View SolutionA gun of mass M fires a bullet of mass m with a velocity v relative to the gun. The average force required to bring the gun to rest in 0.5 sec. is
View SolutionA swimmer wands to cross a river and reach point B directly from A. The speed of the wimmer in still river and that of river flow are same. The dotted line AN is normal to flow direction of river. For swimmer to reach point B, the angle his velocity relative to river will make with line AN is given by θ. then the value of θ is :
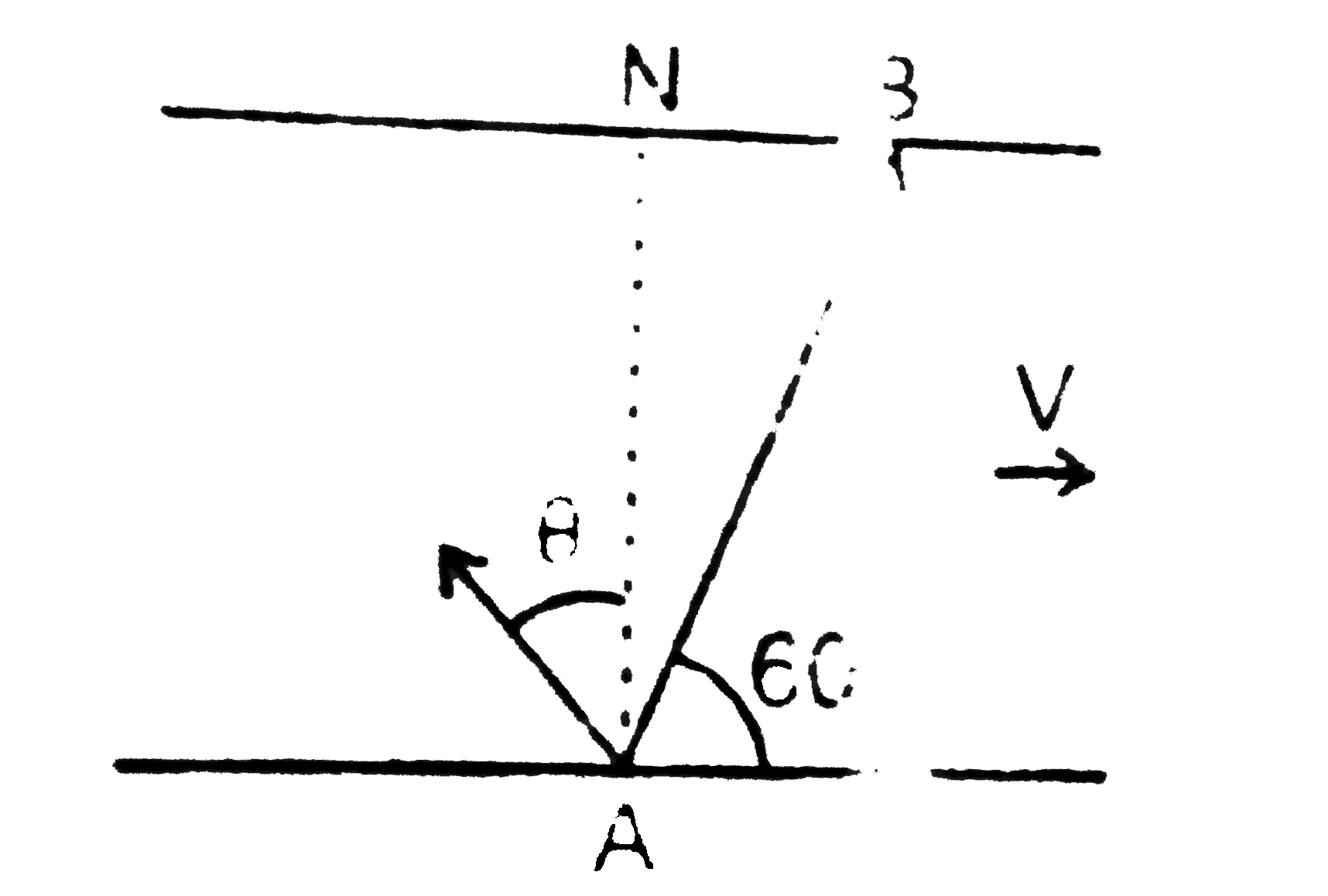 View Solution
View SolutionA swimmer crosses a river with minimum possible time 10 Second. And when he reaches the other end starts swimming in the direction towards the point from where he started swimming. Keeping the direction fixed the swimmer crosses the river in 15 sec. The ratio of speed of swimmer with respect to water and the speed of river flow is (Assume contant speed of river & swimmer)
View SolutionAn under water swimmer is at a depth of 12 m below the surface of water. A bird is at a height of 18 m from the surface of water, directly above his eyes. For the swimmer the bird appears to be at a distance from the surface of water equal to (Refractive Index of water is 4/3)
View SolutionA hollow sphere of volume V is floating on water surface with half immersed in it. What should be the minimum volume of water poured inside the sphere so that the sphere now sinks into the water ?
View SolutionWater flows through a hose (pipe) whose internal diameter is 2 cm at a speed of 1 m/s. What should be the diameter of the nozzle if the water is to emerge at a speed of 4 m/s
View Solution

