A block of mass m is moving down with constant velocity along an inclined plane of inclination θ. What is the work done by external force in pulling the block along the inclined plane through a height h with constant velocity?
To solve the problem, we need to find the work done by an external force in pulling a block of mass m along an inclined plane through a height h with constant velocity. Here is a step-by-step solution:
Step 1: Understand the Forces Acting on the Block
- The block of mass m is moving down the inclined plane with a constant velocity, which means the net force acting on it is zero.
- The gravitational force acting on the block is mg, where g is the acceleration due to gravity.
- The gravitational force can be resolved into two components:
- Parallel to the incline: mgsinθ
- Perpendicular to the incline: mgcosθ
Step 2: Identify the Forces When Pulling the Block Up
- When the block is pulled up the incline, the external force F must overcome both the component of gravitational force acting down the incline and any frictional force.
- Since the block is moving with constant velocity while being pulled, the net force is still zero.
Step 3: Set Up the Equation for Forces
- The equation for forces acting on the block while being pulled up the incline can be written as:
F−mgsinθ−f=0
where f is the frictional force acting up the incline.
Step 4: Relate the Forces
- From the previous step, we can express the external force F as:
F=mgsinθ+f
- Since the block is initially moving down with constant velocity, the frictional force f can be equated to mgsinθ (from the equilibrium condition when moving down):
f=mgsinθ
- Substituting this back into the equation for F:
F=mgsinθ+mgsinθ=2mgsinθ
Step 5: Find the Length of the Incline
- The height h and the length of the incline l are related by the angle θ:
sinθ=hl⇒l=hsinθ
Step 6: Calculate the Work Done
- The work done W by the external force is given by:
W=F⋅l
- Substituting F and l:
W=(2mgsinθ)⋅(hsinθ)
- Simplifying this expression:
W=2mg⋅h
Final Answer
The work done by the external force in pulling the block along the inclined plane through a height h with constant velocity is:
W=2mgh
- The block of mass m is moving down the inclined plane with a constant velocity, which means the net force acting on it is zero.
- The gravitational force acting on the block is mg, where g is the acceleration due to gravity.
- The gravitational force can be resolved into two components:
- Parallel to the incline: mgsinθ
- Perpendicular to the incline: mgcosθ
- When the block is pulled up the incline, the external force F must overcome both the component of gravitational force acting down the incline and any frictional force.
- Since the block is moving with constant velocity while being pulled, the net force is still zero.
- The equation for forces acting on the block while being pulled up the incline can be written as:
F−mgsinθ−f=0
where f is the frictional force acting up the incline.
- From the previous step, we can express the external force F as:
F=mgsinθ+f
- Since the block is initially moving down with constant velocity, the frictional force f can be equated to mgsinθ (from the equilibrium condition when moving down):
f=mgsinθ
- Substituting this back into the equation for F:
F=mgsinθ+mgsinθ=2mgsinθ
- The height h and the length of the incline l are related by the angle θ:
sinθ=hl⇒l=hsinθ
- The work done W by the external force is given by:
W=F⋅l
- Substituting F and l:
W=(2mgsinθ)⋅(hsinθ)
- Simplifying this expression:
W=2mg⋅h
The work done by the external force in pulling the block along the inclined plane through a height h with constant velocity is:
W=2mgh
Similar Questions
A block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.

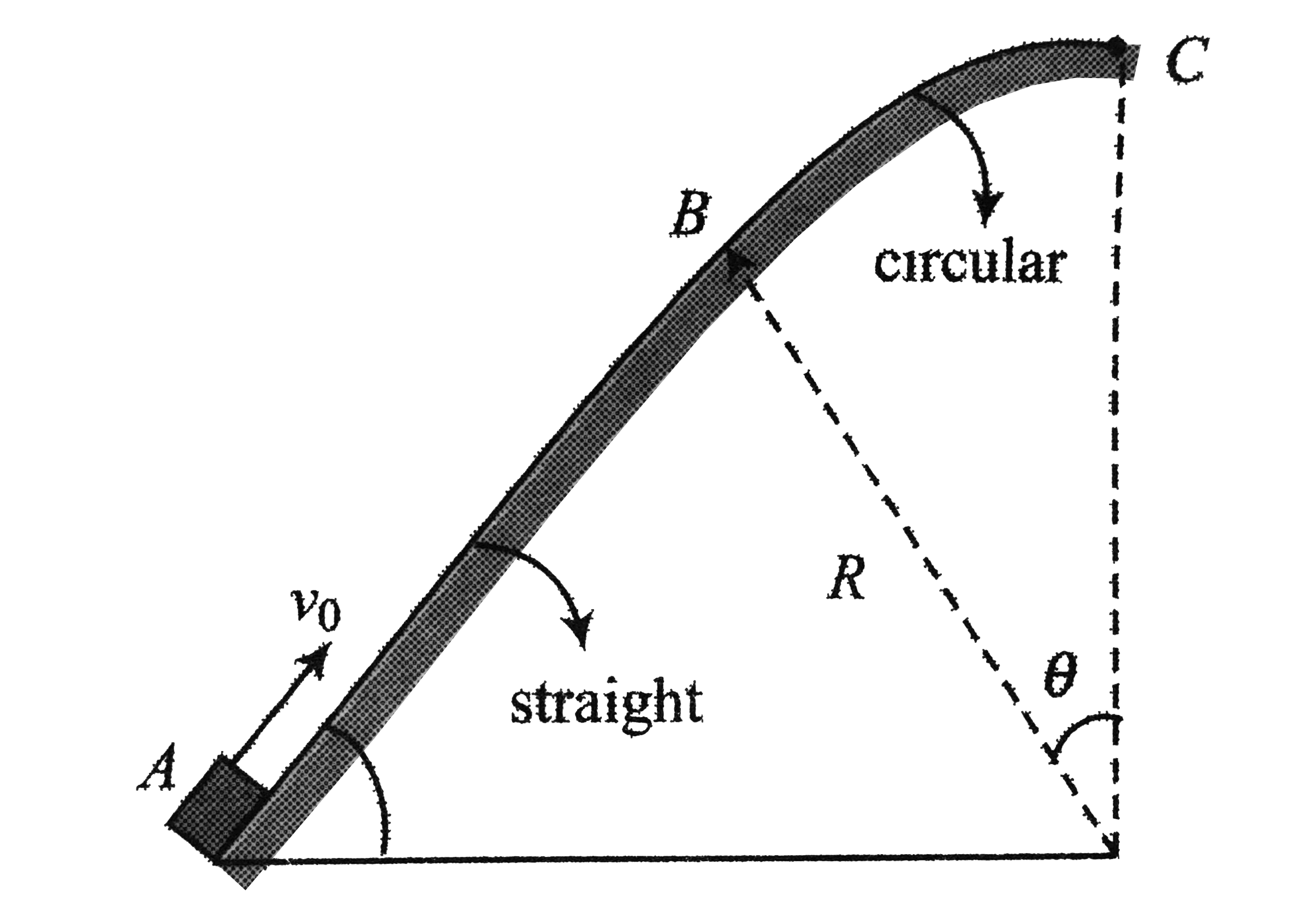
View SolutionA block of mass m is projected up with a velocity v0 along an inclined plane of angle of inclination θ=37∘. The coefficient of friction between the inclined plane AB and blocks is μ(=tanθ). Find the values of v0 so that the block moves in a circular path from B to C.
View SolutionA cubical block of mass M and edge a slides down a rougg inclined plane of inclination θ with a uniform velocity. The torque of the normal force on the block about its centre has magnitude.
View SolutionA cubical block of mass M and edge a slides down a rougg inclined plane of inclination θ with a uniform velocity. The torque of the normal force on the block about its centre has magnitude.
View SolutionThe velocity of a sphere rolling down an inclined plane of height h at an inclination θ with the horizontal, will be :
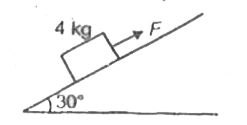
View SolutionA block of mass 4 kg is pulled along a smooth inclined plane of inclination 30∘ with constant velocity 3 m/s as shown, power delivered by the force is
View SolutionA block of mass m is lying on an inclined plane. The coefficient of friction between the plane and the block is μ. The force (F1) required to move the block up the inclined plane will be:-
View SolutionA drum of radius R and mass M, rolls down without slipping along an inclined plane of angle θ. The frictional force-
View SolutionA projectile is fired with a velocity v at right angle to the slope inclined at an angle θ with the horizontal. The range of the projectile along the inclined plane is

View SolutionA block of mass m is kept on an inclined plane is angle inclination θ(<ϕ), where ϕ= angle of friction. Then :

View Solution
