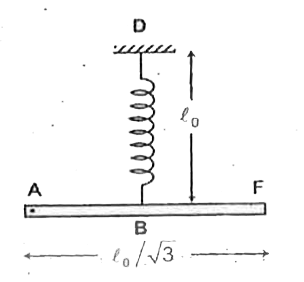
In the figure shown one end of a light spring of natural length $l_{0} = \sqrt{\frac{5}{8}} m (\approx 0.8 m)$ is fixed at point D and other end is attached to the centre B of a uniform rod AF of length $l_{0} / \sqrt{3}$ and mass 10kg. The rod is free to rotate in a vertical plane about a fixed horizontal axis passing through the end A of the rod. The rod is held at rest in horizontal position and the spring is in relaxed state. It is found that, when the rod is released to move it makes an angle of $60^{\circ}$ with the horizontal when it comes to rest for the first time. Find the
(a) the maximum elogation in the spring . (Approximately)
(b) the spring constant. (Approximately)

Video Solution

Text Solution

Verified by Experts

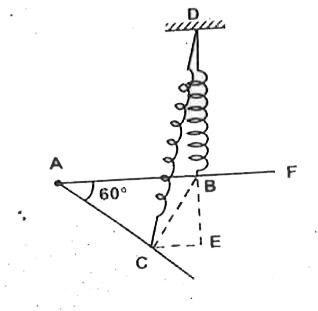
In triangle ABC
$A B = A C$
From geometry in $Δ A B C$
$∴ B C = \frac{l_{0}}{2 \sqrt{3}}$
So, $∠ A B C = ∠ A C B = 60^{\circ}$
Also in triangle $B C D, ∠ D B C = 150^{\circ}$
Applying cosine law
$D C^{2} = D B^{2} + B C^{2} - 2 D B . B C {cos 150}^{\circ}$
$= \frac{5}{8} + \frac{1}{12} \times \frac{5}{8} + 2 \sqrt{\frac{5}{8}} . \frac{1}{2 \sqrt{3}} \times \sqrt{\frac{5}{8}} \times \frac{\sqrt{3}}{2}$
$D C \approx 1 m$
$∴$ Expansion in the spring is $x = 1 - 0.8 \approx 0.2 m$
Vertical displacement of centre of mass of the rod
$B E = A C {sin 60}^{\circ} = \frac{l_{0}}{2 \sqrt{3}} (\frac{\sqrt{3}}{2}) = 0.2 m$
Using conservation of mechanical energy
$M g (B E) = \frac{1}{2} k x^{2}$
$10 \times 10 \times 0.2 = \frac{1}{2} k {(0.2)}^{2}$
$\Rightarrow K = 10^{3} N / m$
$\Rightarrow k \approx 10^{3} N / m$

|

Updated on:21/07/2023

Class 12 PHYSICS WORK, ENERGY AND POWER

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile