For stable equilibrium, which of the following is/are true ?
dUdx=0 and d2Udx2>0
dUdx=0 only
dUdx=0 and d2Udx2<0
None of these
The correct Answer is:C
To determine the conditions for stable equilibrium, we can break down the problem into a series of logical steps:
1. Understanding Stable Equilibrium:
- Stable equilibrium occurs when a system returns to its original position after being slightly disturbed. This implies that the net force acting on the body is zero.
- Mathematically, this can be expressed as:
Fnet=0
2. Forces Acting on the Body:
- Consider a body placed on a parabolic path. The forces acting on the body include:
- The gravitational force acting downward, mg.
- The normal force acting upward, N.
- For stable equilibrium, these forces must balance:
N=mg
3. Restoring Force Concept:
- When the body is displaced from its equilibrium position, a restoring force acts to bring it back to equilibrium. This restoring force can be defined as:
F=−dudx
- For stable equilibrium, the condition for the net force to be zero leads us to:
dudx=0
4. Second Derivative Condition:
- To ensure that the equilibrium is stable, we need to check the concavity of the potential energy function u. This is done by examining the second derivative:
d2udx2<0
- This condition indicates that the potential energy function is at a minimum, which is characteristic of stable equilibrium.
5. Conclusion:
- Therefore, for stable equilibrium, the following conditions must be satisfied:
- The first derivative of potential energy with respect to position must be zero:
dudx=0
- The second derivative of potential energy with respect to position must be less than zero:
d2udx2<0
- Stable equilibrium occurs when a system returns to its original position after being slightly disturbed. This implies that the net force acting on the body is zero.
- Mathematically, this can be expressed as:
Fnet=0
- Consider a body placed on a parabolic path. The forces acting on the body include:
- The gravitational force acting downward, mg.
- The normal force acting upward, N.
- For stable equilibrium, these forces must balance:
N=mg
- When the body is displaced from its equilibrium position, a restoring force acts to bring it back to equilibrium. This restoring force can be defined as:
F=−dudx
- For stable equilibrium, the condition for the net force to be zero leads us to:
dudx=0
- To ensure that the equilibrium is stable, we need to check the concavity of the potential energy function u. This is done by examining the second derivative:
d2udx2<0
- This condition indicates that the potential energy function is at a minimum, which is characteristic of stable equilibrium.
- Therefore, for stable equilibrium, the following conditions must be satisfied:
- The first derivative of potential energy with respect to position must be zero:
dudx=0
- The second derivative of potential energy with respect to position must be less than zero:
d2udx2<0
Similar Questions
Knowledge Check
Which of the following is the least stable?
A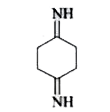 B
B C
C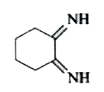 D
D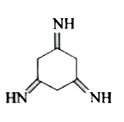
Which of the following is least stable ?
View SolutionWhich of the following ions is more stable ?
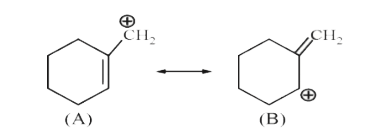
View SolutionWhich of the following is most stable ?
View SolutionWhich of the following is least stable?
View SolutionWhich of the following is least stable
View SolutionWhich of the following is most stable?
View SolutionWhich of the following is stable (inert) to fire ?
View Solution
