The energy needed for breaking a drop of radius R into n drops each of radius r is
(4πr2−4πR2)T
(4πR2−4πr2)T
[43πr3−43πR3]T
(4πr2−n4πr2)/T
The correct Answer is:A
To find the energy needed for breaking a drop of radius R into n drops each of radius r, we can follow these steps:
Step 1: Understand the concept of surface tension
Surface tension (T) is the energy required to create a unit area of surface. When a drop is broken into smaller drops, the surface area increases, and thus energy is required to create this new surface area.
Step 2: Calculate the initial energy
The initial drop has a radius R. The surface area Ai of the initial drop is given by the formula for the surface area of a sphere:
Ai=4πR2
The initial energy (Ei) associated with this surface area is:
Ei=T×Ai=T×4πR2
Step 3: Calculate the final energy
When the drop is broken into n smaller drops, each of radius r, the surface area Af of one small drop is:
Af=4πr2
Since there are n such drops, the total surface area for all n drops is:
Af=n×Af=n×4πr2
The final energy (Ef) associated with this total surface area is:
Ef=T×Af=T×n×4πr2
Step 4: Calculate the energy required for breaking the drop
The energy required (E) to break the original drop into n smaller drops is the difference between the final energy and the initial energy:
E=Ef−Ei
Substituting the expressions for Ef and Ei:
E=(T×n×4πr2)−(T×4πR2)
Factoring out T:
E=T×(n×4πr2−4πR2)
This can be simplified to:
E=4πT×(nr2−R2)
Final Answer
Thus, the energy needed for breaking a drop of radius R into n drops each of radius r is:
E=4πT(nr2−R2)
---
Surface tension (T) is the energy required to create a unit area of surface. When a drop is broken into smaller drops, the surface area increases, and thus energy is required to create this new surface area.
The initial drop has a radius R. The surface area Ai of the initial drop is given by the formula for the surface area of a sphere:
Ai=4πR2
The initial energy (Ei) associated with this surface area is:
Ei=T×Ai=T×4πR2
When the drop is broken into n smaller drops, each of radius r, the surface area Af of one small drop is:
Af=4πr2
Since there are n such drops, the total surface area for all n drops is:
Af=n×Af=n×4πr2
The final energy (Ef) associated with this total surface area is:
Ef=T×Af=T×n×4πr2
The energy required (E) to break the original drop into n smaller drops is the difference between the final energy and the initial energy:
E=Ef−Ei
Substituting the expressions for Ef and Ei:
E=(T×n×4πr2)−(T×4πR2)
Factoring out T:
E=T×(n×4πr2−4πR2)
This can be simplified to:
E=4πT×(nr2−R2)
Thus, the energy needed for breaking a drop of radius R into n drops each of radius r is:
E=4πT(nr2−R2)
Similar Questions
Knowledge Check
Energy needed in breaking a drop of radius R into n drops of radius r, is where T is surface tension and P is atmospheric pressure.
A(4πr2n−4πR2)TB(4π3nr2−43πR2)TC(4πR2−4πr2)nTD(4πR2−n4πr2)P
If a drop of liquid breaks into smaller droplets, it result in lowering of temperature of the droplets. Let a drop of radius R, breaks into N small droplets each of radius r. Estimate the drop in temperature.
View SolutionWork done in forming a liquid drop of radius R is W1 and that of radius 3R is W2. The ratio of work done is
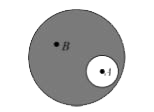
View SolutionThere is an air bubble of radius R inside a drop of water of radius 3R. Find the ratio of gauge pressure at point B to that at point A.
View SolutionThe kinetic energy needed to project a body of mass m from the earth surface (radius R) to infinity is
View SolutionThe work done to split a liquid drop id radius R into N identical drops is (taken σ as the surface tension of the liquid)
View SolutionA force F is needed to break a copper wire having radius R. The force needed to break a copper wire of same length and radius 2R will be
View Solutionn number of water droplets, each of radius r, coalese, to form a single drop of radius R. The rise in temperature dθ is
View Solution
