Chosse the correct statement (s) about the pressure in a liquid .
Two points in the same horizontal plane can not have te same pressure
Two points at different levels may have same pressure
two points at different levels canot have same pressure
Two points in the same vertical line always have different pressures
The correct Answer is:B
To solve the question regarding the correct statements about pressure in a liquid, we will analyze the statements step by step.
Step 1: Understanding Pressure in a Liquid
In a liquid at rest (static fluid), the pressure at a given depth is the same at all points on a horizontal plane. This means that if two points are at the same horizontal level in a non-accelerated fluid, they will have the same pressure.
Hint: Remember that pressure in a static fluid depends only on the depth, not the horizontal position.
Step 2: Analyzing the Statements
1. Statement A: "Two points in the same horizontal plane cannot have the same pressure."
- This statement is incorrect because, in a static fluid, points at the same horizontal level do have the same pressure.
2. Statement B: "Two points at different levels may have the same pressure."
- This statement is correct. In certain conditions (e.g., when the fluid is moving), two points at different heights can have the same pressure due to the dynamics of fluid flow.
3. Statement C: "Two points in the same vertical line cannot have the same pressure."
- This statement is incorrect. In a static fluid, two points in the same vertical line (but at different depths) will have different pressures. However, in a dynamic fluid, it is possible for two points along the same vertical line to have the same pressure if the conditions allow for it.
Step 3: Conclusion
Based on the analysis:
- Statement A is incorrect.
- Statement B is correct.
- Statement C is incorrect.
Thus, the only correct statement is Statement B.
Final Answer:
The correct statement about the pressure in a liquid is Statement B: "Two points at different levels may have the same pressure."
In a liquid at rest (static fluid), the pressure at a given depth is the same at all points on a horizontal plane. This means that if two points are at the same horizontal level in a non-accelerated fluid, they will have the same pressure.
1. Statement A: "Two points in the same horizontal plane cannot have the same pressure."
- This statement is incorrect because, in a static fluid, points at the same horizontal level do have the same pressure.
- This statement is correct. In certain conditions (e.g., when the fluid is moving), two points at different heights can have the same pressure due to the dynamics of fluid flow.
- This statement is incorrect. In a static fluid, two points in the same vertical line (but at different depths) will have different pressures. However, in a dynamic fluid, it is possible for two points along the same vertical line to have the same pressure if the conditions allow for it.
Based on the analysis:
- Statement A is incorrect.
- Statement B is correct.
- Statement C is incorrect.
The correct statement about the pressure in a liquid is Statement B: "Two points at different levels may have the same pressure."
Similar Questions
Knowledge Check
Chosse the incorrect statement.
AThe Montreal protocol is associated with the control of emission of ozone depleting substances.BMethane and carbon dioxide are greenhouse gases.CDobson units are used to measure oxygen content.DUse of incinertators is crucial to disposal of hospital wastes.
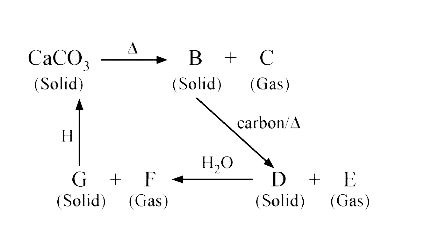
The correct statement about F is
View SolutionCorrect statements (s) about
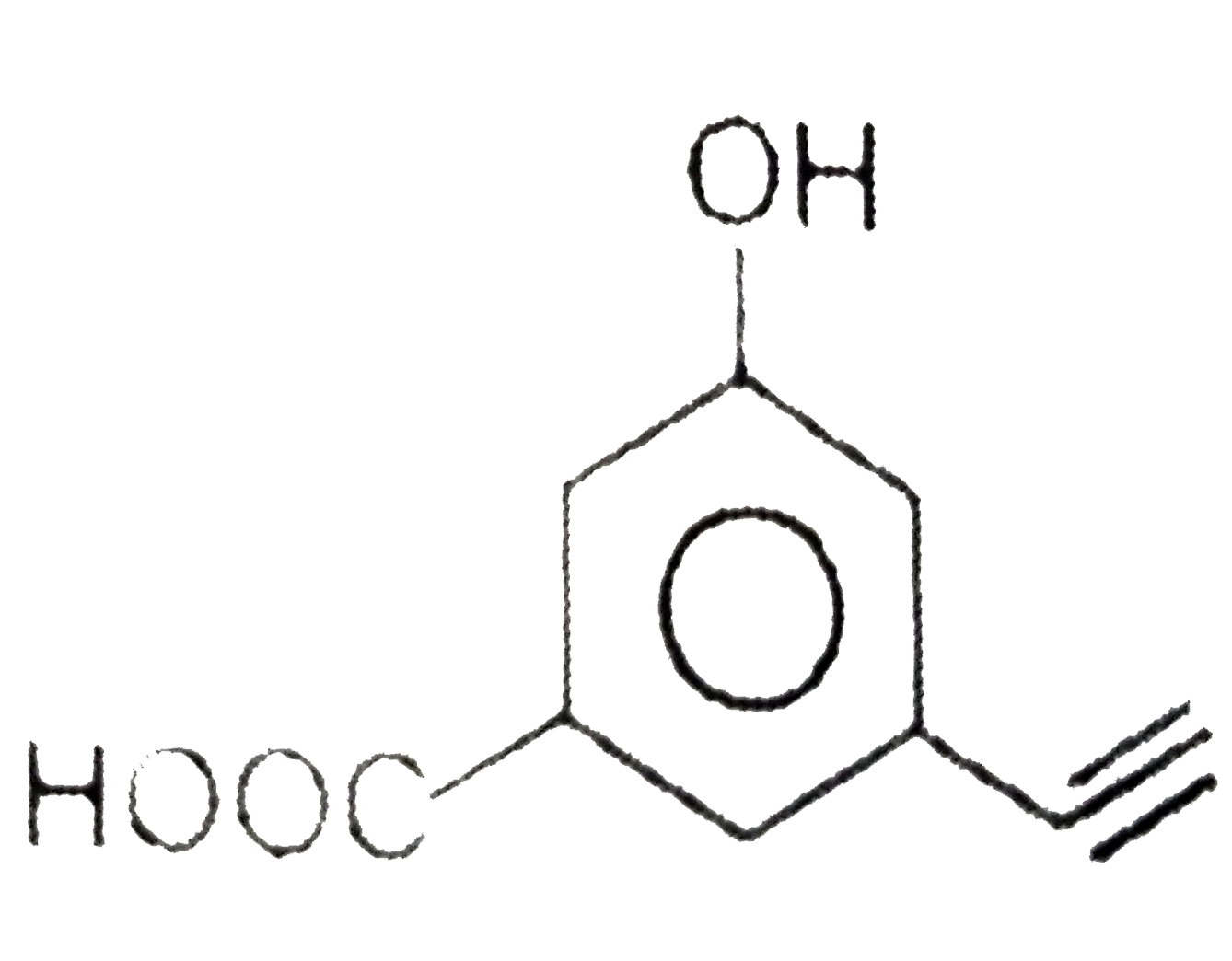is /are
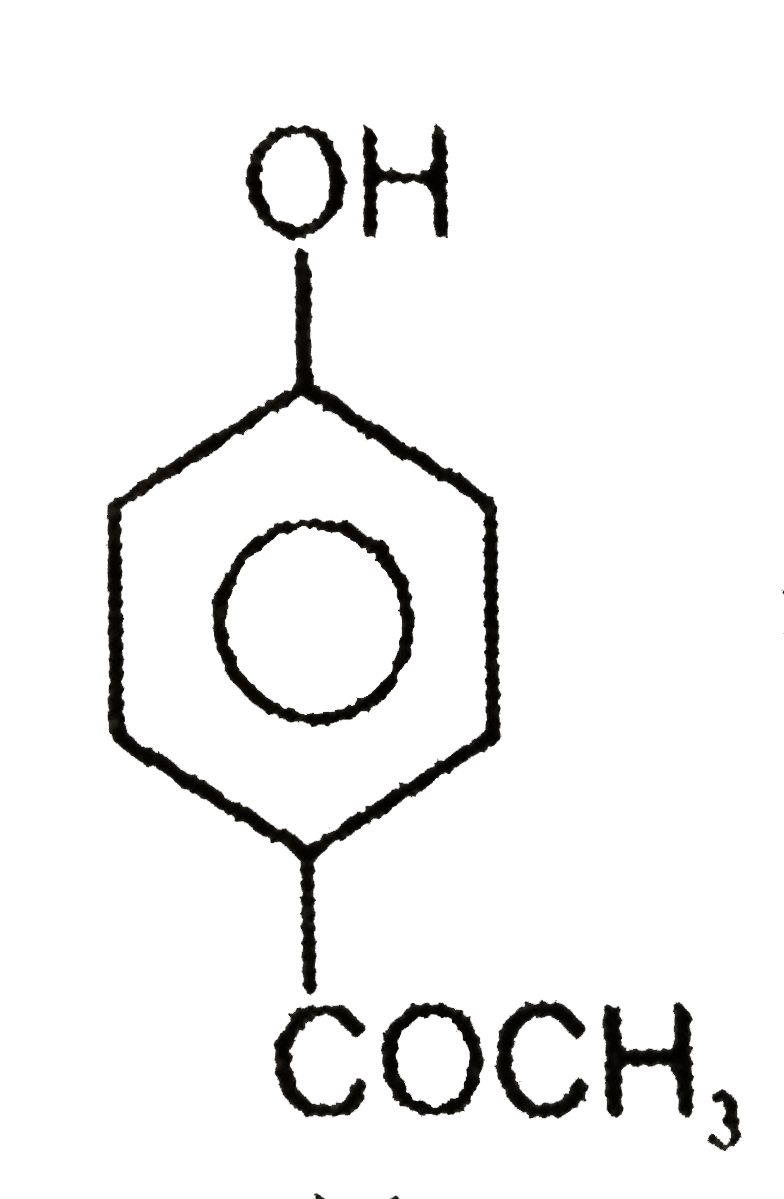
View SolutionCorrect statements (s) about
is /are
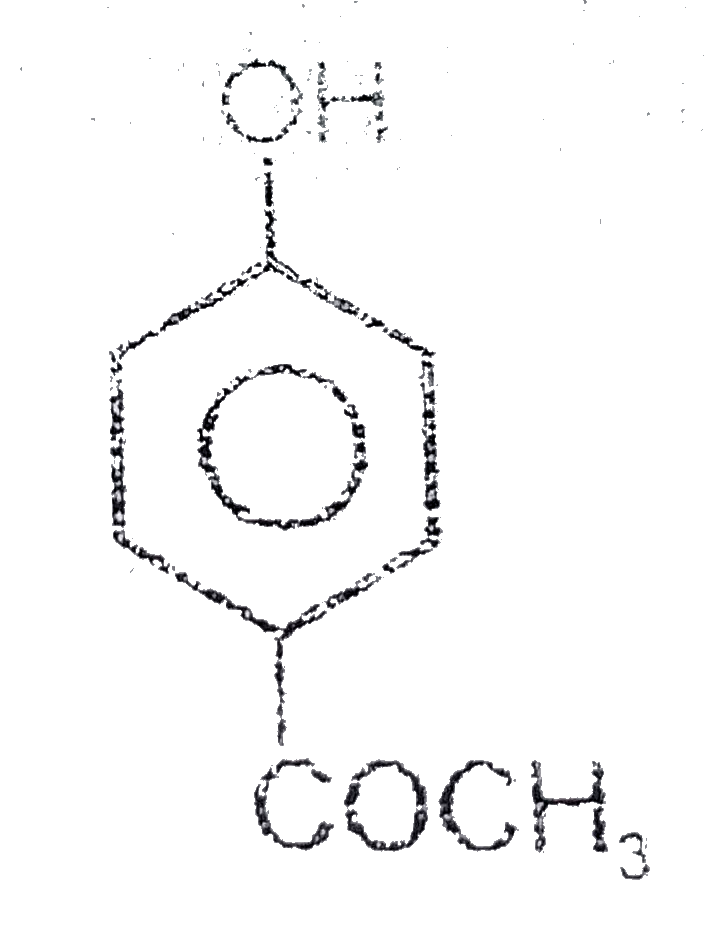
View SolutionCorrect statement (s) about
is/are
View SolutionThe correct statements about anomers are
View SolutionThe correct statements about peptides are
View SolutionFigure shows a container filled with a liquid of density ρ. Four points A,B,C and D lie on the vertices of a vertical square. Points A and C lie on a vertical line and points B and D lies on a horizontal line. Choose the correct statement(s) about the pressure at the four points.
View Solution