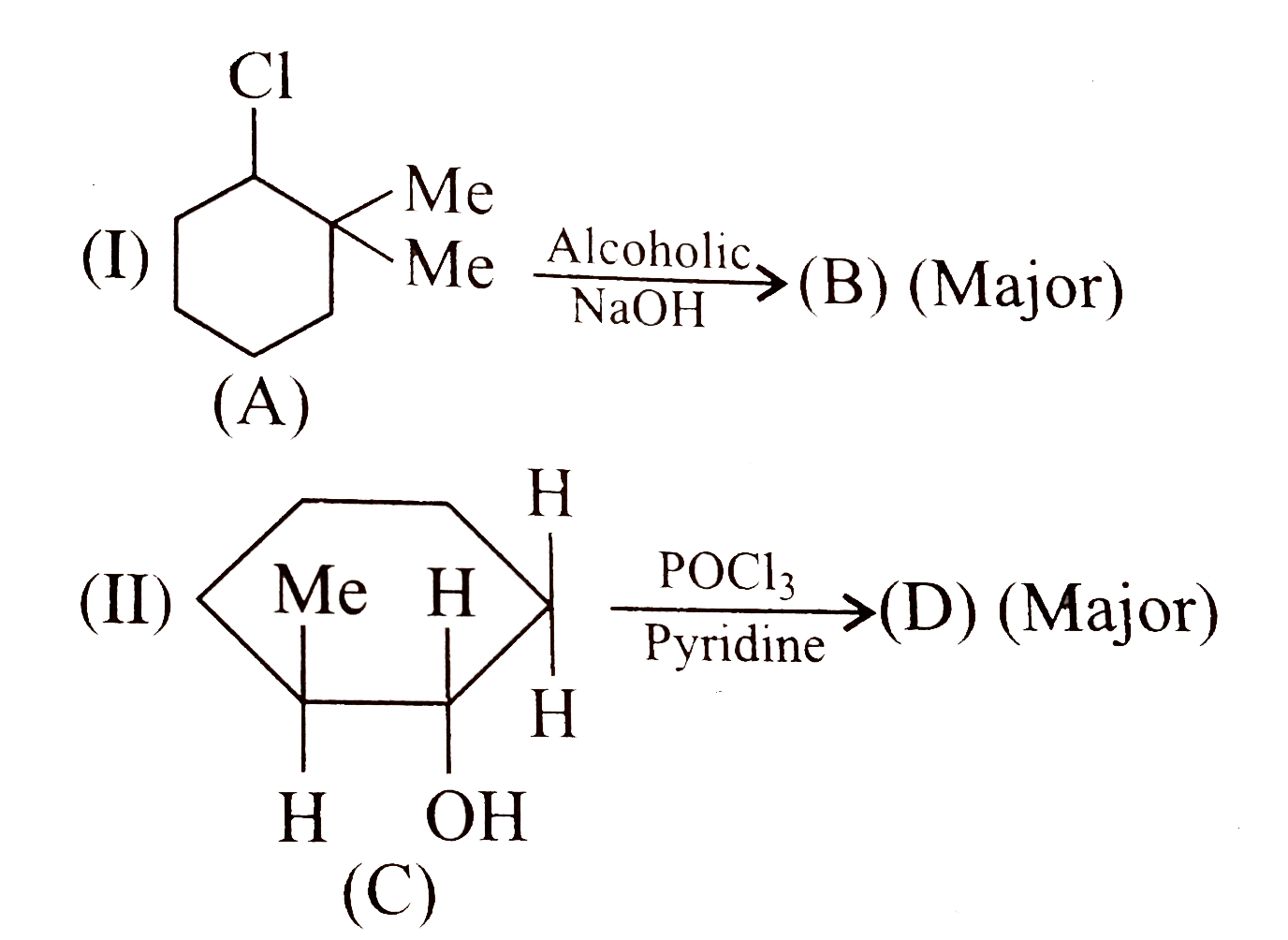
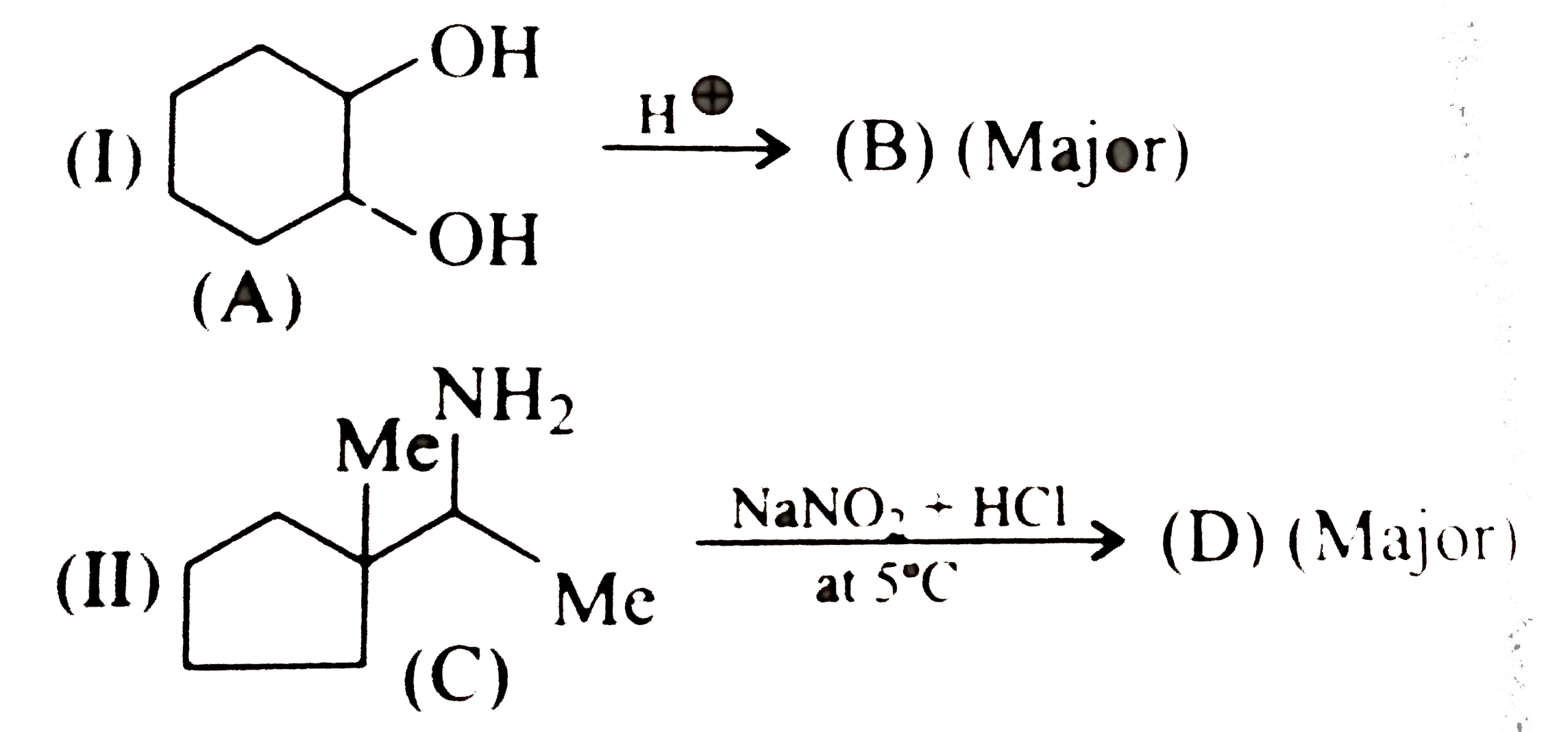Consider an attractive force which is central but is inversely proportional to the first power of distance. If a particle is in circular orbit, under such a force , which of the following statements are correct ?
the speed is directly proportional to the square root of orbital radius
the speed isindependent of radius
the period is independent of radius
the period is directly proportional to radius.
The correct Answer is:B, D
To solve the problem, we need to analyze the given attractive force, which is inversely proportional to the first power of distance. Let's denote this force as F. According to the problem, we can express this force as:
F=kr
where k is a constant and r is the distance from the center of the force.
Step 1: Equate the gravitational force to the centripetal force
For a particle in circular motion, the centripetal force required to keep the particle in orbit is given by:
Fc=mv2r
where m is the mass of the particle and v is its speed. Since the attractive force F provides the necessary centripetal force, we can set these two forces equal:
kr=mv2r
Step 2: Simplify the equation
We can cancel r from both sides of the equation (assuming r≠0):
k=mv2
From this equation, we can solve for the speed v:
v2=km
Taking the square root gives us:
v=√km
Step 3: Analyze the speed
From the expression for v, we see that the speed v is independent of the radius r. This means that regardless of how far the particle is from the center, its speed remains constant.
Step 4: Determine the time period
The time period T of the circular motion can be found using the relationship between speed, distance, and time. The distance traveled in one complete orbit (circumference of the circle) is 2πr, so we have:
T=DistanceSpeed=2πrv
Substituting the expression for v:
T=2πr√km=2πr√mk
Step 5: Analyze the time period
From the expression for T, we can see that the time period T is directly proportional to the radius r. This means that as the radius increases, the time period also increases.
Conclusion
Based on our analysis, we can summarize the findings:
1. The speed v is independent of the radius r.
2. The time period T is directly proportional to the radius r.
Thus, the correct statements are:
- Speed is independent of the radius (Option 2 is correct).
- Time period is directly proportional to the radius (Option 4 is correct).
Final Answer
The correct options are 2 and 4.
For a particle in circular motion, the centripetal force required to keep the particle in orbit is given by:
We can cancel r from both sides of the equation (assuming r≠0):
From the expression for v, we see that the speed v is independent of the radius r. This means that regardless of how far the particle is from the center, its speed remains constant.
The time period T of the circular motion can be found using the relationship between speed, distance, and time. The distance traveled in one complete orbit (circumference of the circle) is 2πr, so we have:
From the expression for T, we can see that the time period T is directly proportional to the radius r. This means that as the radius increases, the time period also increases.
Based on our analysis, we can summarize the findings:
2. The time period T is directly proportional to the radius r.
- Speed is independent of the radius (Option 2 is correct).
- Time period is directly proportional to the radius (Option 4 is correct).
The correct options are 2 and 4.
Similar Questions
Knowledge Check
Consider the following conformations. Which of the following statements is correct?
 AStructure I represents staggered conformation.BStructure Il represents a skew conformationCStructure Ill represents eclipsed conformation.DI, II and III are the conformations of propane.
AStructure I represents staggered conformation.BStructure Il represents a skew conformationCStructure Ill represents eclipsed conformation.DI, II and III are the conformations of propane.Which of the following statements is true about electrical forces?
AElectrical forces are produced by electrical charges.BLike charges attract, unlike charges repel.CElectric forces are weaker than gravitational forces.DPositive and negative charges can combine to produce a third type of charge.
Consider the following compounds Which of the following statements are correct?
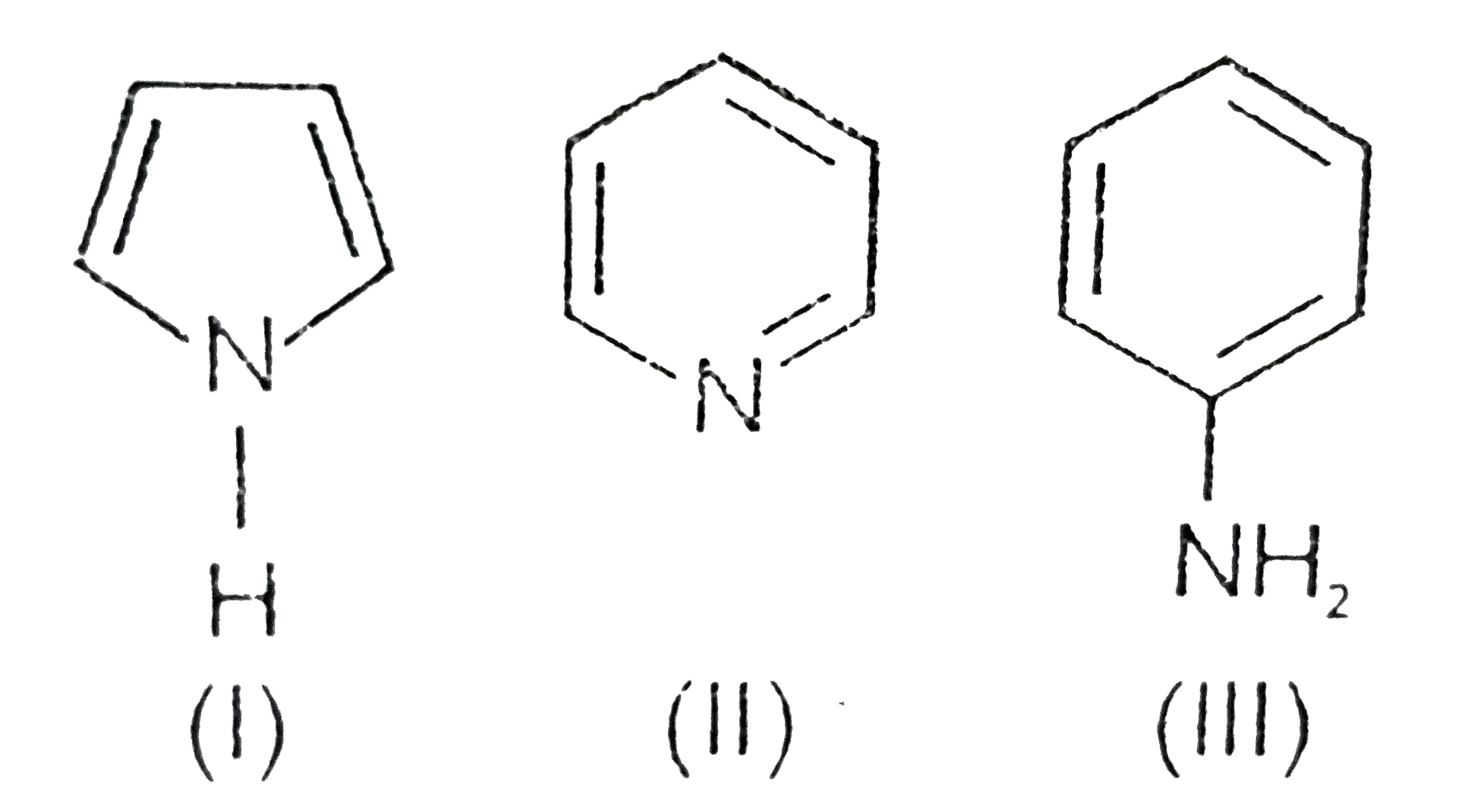
View SolutionWhich of the following statement regarding an orbital is correct ?
View SolutionWhich of the following statements is true for nuclear forces?
View SolutionWhich of the following statements is incorrect for nuclear forces?
View SolutionWhich of the following is correct about nuclear forces?
View SolutionThe force acting on a body is inversely proportional to the distance (x) covered. The work done is proportional to
View Solution