The earth, moving around the sun in a circular orbit, is acted upon by a force and hence work must be done on earth by this force.
To solve the problem, we need to analyze the situation of the Earth moving around the Sun in a circular orbit and determine whether work is done on the Earth by the gravitational force exerted by the Sun.
1. Understanding the Forces Involved:
- The Earth is in a circular orbit around the Sun due to the gravitational force exerted by the Sun. This force acts as the centripetal force that keeps the Earth in its circular path.
2. Identifying the Direction of Forces and Displacement:
- The gravitational force (Fg) acts towards the center of the Sun. At any point in its orbit, the Earth has a velocity that is tangential to the circular path. Therefore, the direction of the gravitational force is radial (inward), while the displacement of the Earth is tangential to the orbit.
3. Analyzing the Work Done:
- Work done (W) by a force is given by the formula:
W=F⋅d⋅cos(θ)
where F is the force, d is the displacement, and θ is the angle between the force and the displacement vectors.
- In this case, since the gravitational force is directed towards the center and the displacement is tangential, the angle θ between the gravitational force and the displacement is 90∘.
4. Calculating Work Done:
- Since cos(90∘)=0, we can conclude that:
W=Fg⋅d⋅cos(90∘)=0
- Therefore, the work done by the gravitational force on the Earth is zero.
5. Conclusion:
- Since the work done is zero, it implies that there is no change in the kinetic energy of the Earth as it moves in its orbit. The total mechanical energy (kinetic + potential) of the Earth remains constant while it is in orbit.
Final Answer:
The work done on the Earth by the gravitational force exerted by the Sun is zero.
---
- The Earth is in a circular orbit around the Sun due to the gravitational force exerted by the Sun. This force acts as the centripetal force that keeps the Earth in its circular path.
- The gravitational force (Fg) acts towards the center of the Sun. At any point in its orbit, the Earth has a velocity that is tangential to the circular path. Therefore, the direction of the gravitational force is radial (inward), while the displacement of the Earth is tangential to the orbit.
- Work done (W) by a force is given by the formula:
W=F⋅d⋅cos(θ)
where F is the force, d is the displacement, and θ is the angle between the force and the displacement vectors.
- In this case, since the gravitational force is directed towards the center and the displacement is tangential, the angle θ between the gravitational force and the displacement is 90∘.
- Since cos(90∘)=0, we can conclude that:
W=Fg⋅d⋅cos(90∘)=0
- Therefore, the work done by the gravitational force on the Earth is zero.
- Since the work done is zero, it implies that there is no change in the kinetic energy of the Earth as it moves in its orbit. The total mechanical energy (kinetic + potential) of the Earth remains constant while it is in orbit.
The work done on the Earth by the gravitational force exerted by the Sun is zero.
Similar Questions
Knowledge Check
An earth satellite is moving around the earth in circular orbit. IN such case what is conserved
AvelocityBlinear momentumCangular momentumDnone of the aboveThe earth moves around the Sun in an elliptical orbit as shown in Fig. The ratio OA/OB=x. The ratio of the speed of the earth at B to that at A is nearly
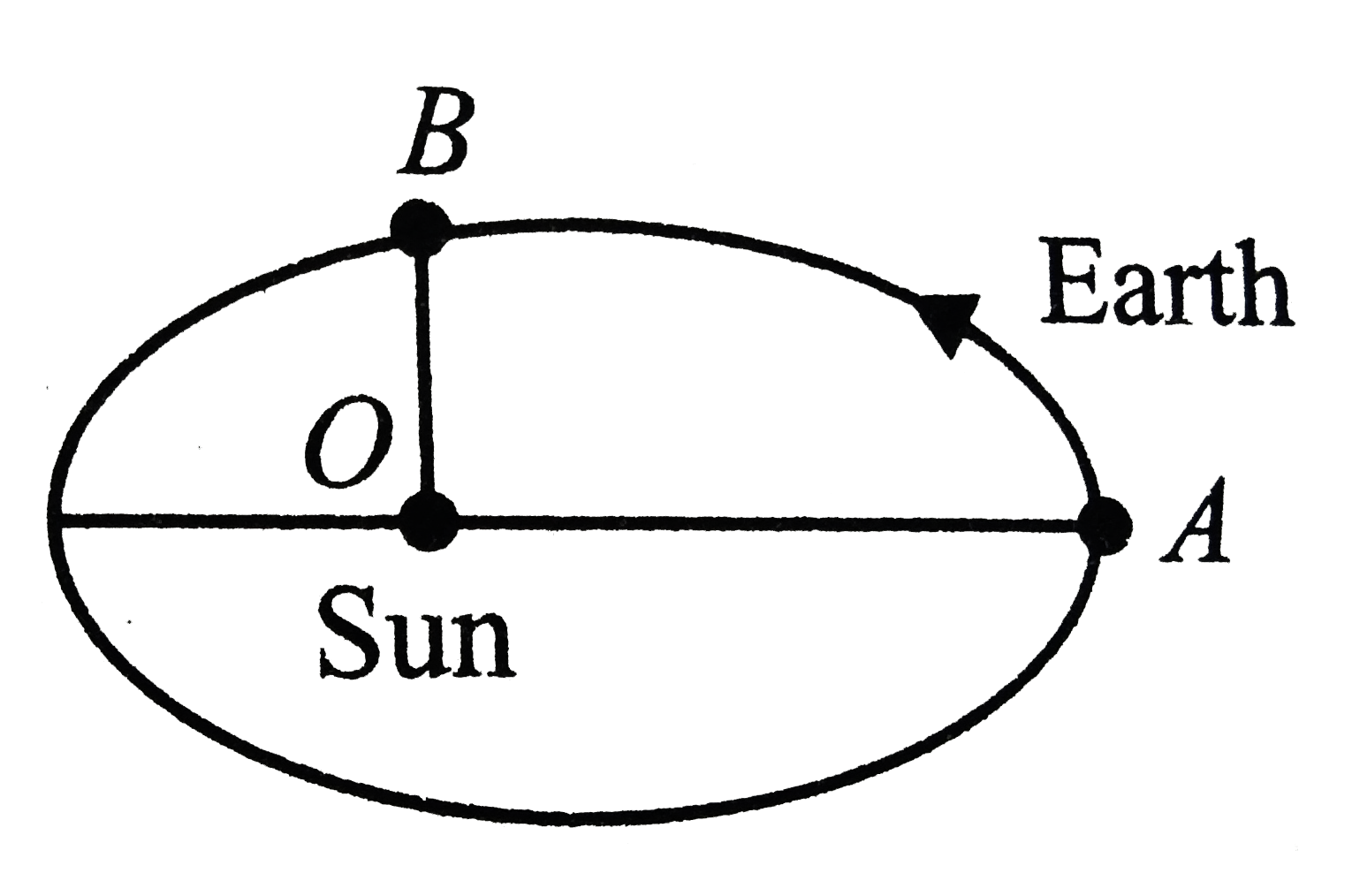 A√xBxCx√xDx2
A√xBxCx√xDx2A satellite is moving around the earth with speed v in a circular orbit of radius r. IF the orbit radius is decreased by 1%, its speed will
Aincrease by 1%Bincrease by 0.5 %Cdecrease by 1%Ddecrease by 0.5 %
Assertion(A) : The earth revolves around the sun an elliptical orbit
Reasoning(R) : The sun alwaye attracts the earth with the same force
View SolutionEarth completes one orbit around the sun is
View SolutionStarting at rest , a10kg object is acted upon by only one force as indicated in figure. Then the total work done by the force is :
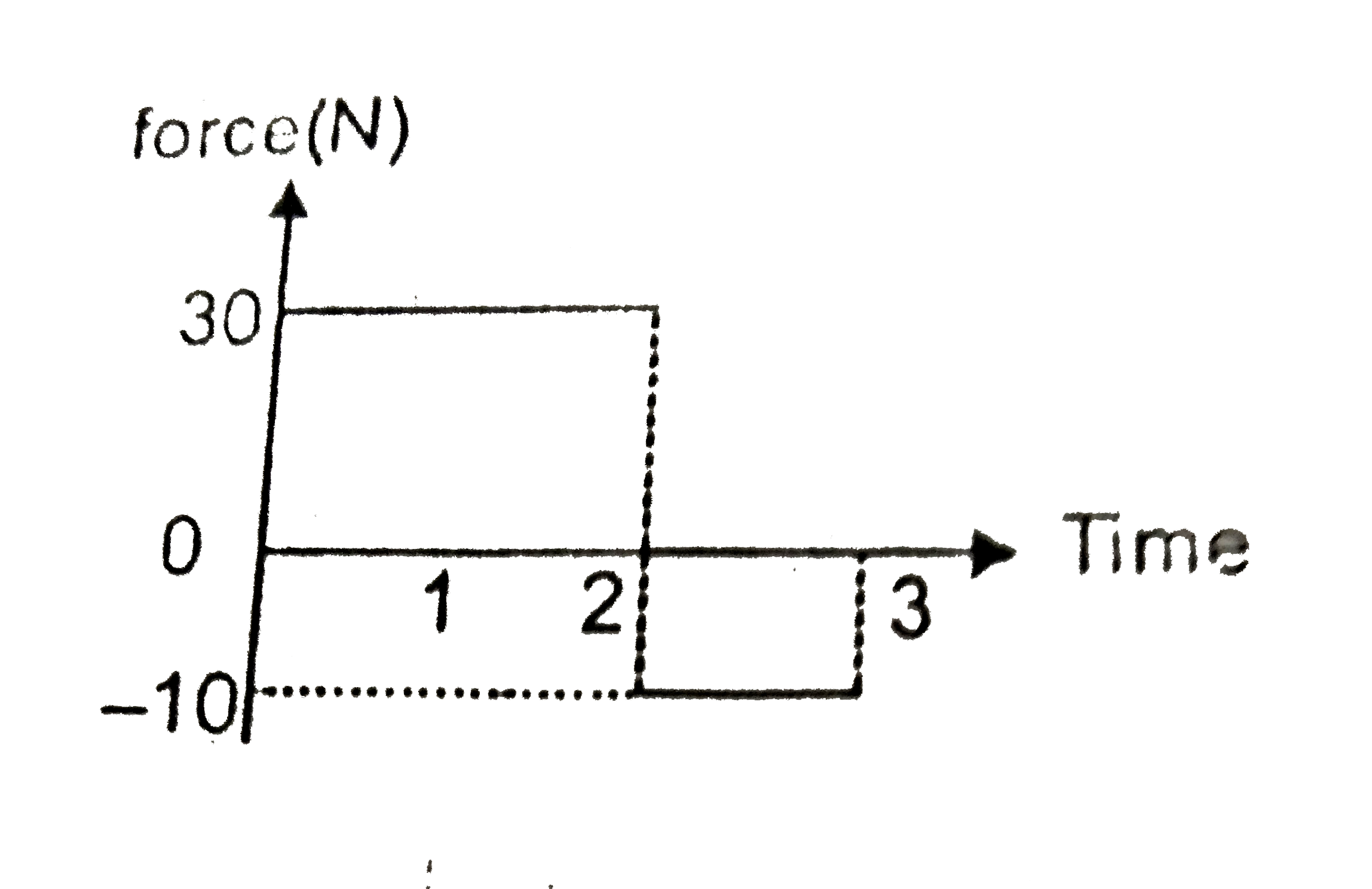
View SolutionStarting from rest a 10 kg object is acted upon by only one force as indicated in figure. Then the total work done by the force in 5 seconds is

View SolutionA satellite X moves round the earth in a circular orbit of radius R. If another satellite Y of the same mass moves round the earth in a circular orbit of radius 4R, then the speed of X is ____________ times that of Y.
View Solution
