The earth revolves round the sun in an elliptical orbit. Its speed
goes on decreasing continuously
greatest when it is closest to the sun
greatest when it is farthest from the sun
constant at all the points on the orbit
The correct Answer is:B
To solve the problem regarding the speed of the Earth as it revolves around the Sun in an elliptical orbit, we can follow these steps:
1. Understanding the Orbit: The Earth revolves around the Sun in an elliptical orbit. An ellipse has two foci, and one of them is occupied by the Sun.
2. Forces Acting on the Earth: The only force acting on the Earth is the gravitational attraction exerted by the Sun. This force is directed towards the Sun.
3. Torque Consideration: Since the gravitational force acts along the line connecting the Earth and the Sun, there is no torque about the Sun. This means that the angular momentum of the Earth is conserved.
4. Angular Momentum Conservation: The angular momentum (L) of the Earth can be expressed as:
L=m⋅v⋅r
where m is the mass of the Earth, v is the velocity of the Earth, and r is the distance from the Earth to the Sun.
5. Constant Angular Momentum: Since angular momentum is conserved, we can say that:
m⋅v⋅r=constant
This implies that as r changes, v must change in such a way that the product v⋅r remains constant.
6. Analyzing the Relationship: When the Earth is closest to the Sun (at perihelion), the distance r is at its minimum. Since m is constant, for the product m⋅v⋅r to remain constant, if r decreases, v must increase. Conversely, when the Earth is farthest from the Sun (at aphelion), r is at its maximum, and thus v must decrease.
7. Conclusion: Therefore, the speed of the Earth is greatest when it is closest to the Sun and least when it is farthest from the Sun. This leads us to conclude that the speed of the Earth varies inversely with the distance from the Sun.
Final Answer:
The speed of the Earth is greatest when it is closest to the Sun and decreases as it moves away from the Sun.
---
L=m⋅v⋅r
where m is the mass of the Earth, v is the velocity of the Earth, and r is the distance from the Earth to the Sun.
m⋅v⋅r=constant
This implies that as r changes, v must change in such a way that the product v⋅r remains constant.
The speed of the Earth is greatest when it is closest to the Sun and decreases as it moves away from the Sun.
Similar Questions
Assertion(A) : The earth revolves around the sun an elliptical orbit
Reasoning(R) : The sun alwaye attracts the earth with the same force
View SolutionA planet is revolving around the Sun in an elliptical orbit. Its closest distance from the Sun is r and farthest distance is R. If the orbital velocity of the planet closest to the Sun is v, then what is the velocity at the farthest point?
View Solution
Knowledge Check
A planet revolves around the sun in an elliptical orbit. If vp and va are the velocities of the planet at the perigee and apogee respectively, then the eccentricity of the elliptical orbit is given by :
AvpvaBva−vpva+vpCvp+vavp−vaDvp−vavp+vaThe earth moves around the Sun in an elliptical orbit as shown in Fig. The ratio OA/OB=x. The ratio of the speed of the earth at B to that at A is nearly
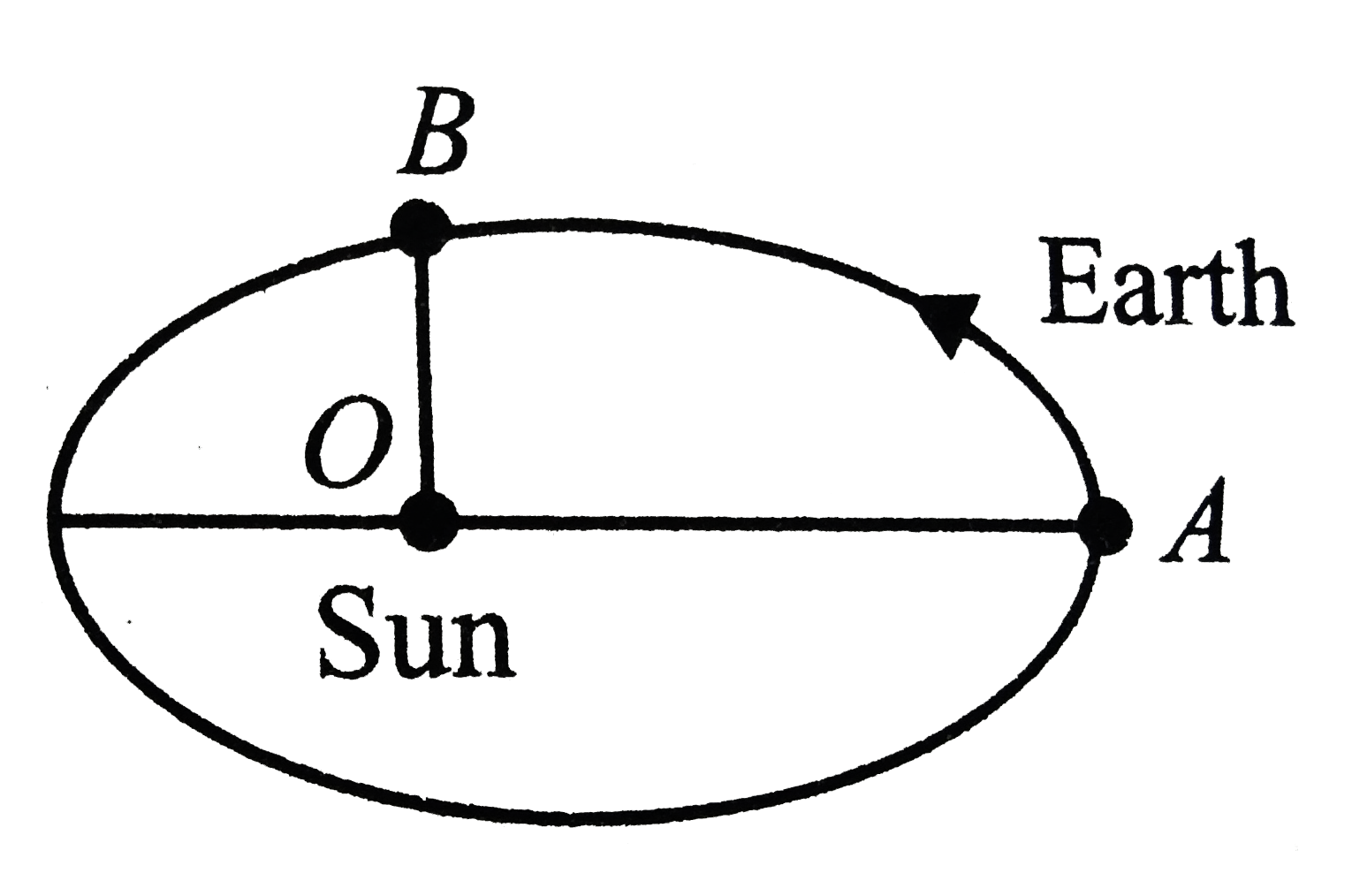 A√xBxCx√xDx2
A√xBxCx√xDx2A planet revolves around the sun in an elliptical orbit. Suppose that the gravitational attraction between the sun and the planet suddenly disappear then the planet would move
Atowards the sun in a spiral pathBaway from the sun along a straight path with continuously increasing speedCwith constant speed along a tangential path to the oribtDtowards the sun along a straight path with constant speed
A planet is revolving around the Sun in an elliptical orbit. Its closest distance from the sun is rmin. The farthest distance from the sun is rmax if the orbital angular velocity of the planet when it is nearest to the Sun ω then the orbital angular velocity at the point when it is at the farthest distance from the sun is
View SolutionA comet revolves around the sun in an eliptical orbit. When it is closest to the sun at a distance d, its corresponding kinetic energy is k0. If it is farthest from the sun at distance 3d then the corresponding kinetic energy will be
View SolutionFollowing physical quantity is constant where a planet that revolves around Sun in an elliptical orbit.
View SolutionA planet revolves around the sun in an elliptical . The linear speed of the planet will be maximum at

View SolutionA planet is revolving round the sun in an elliptical orbit, If v is the velocity of the planet when its position vector from the sun is r, then areal velocity of the planet is
View Solution
