Three point masses are at the corners of an equilateral traingle of side r. Their separations do not change when the system rotates about the centre of the triangle. For this, the time period of rotation must be proportional to
r3/2
r
m
m−1/2
The correct Answer is:A, D
To solve the problem, we need to find the relationship between the time period of rotation of three point masses located at the corners of an equilateral triangle and the parameters involved, namely the side length r of the triangle and the mass m of the point masses.
1. Understand the System:
We have three point masses m located at the corners of an equilateral triangle with side length r. The system rotates about the centroid of the triangle.
2. Calculate the Gravitational Force:
The gravitational force between any two masses m is given by:
F0=Gm2r2
where G is the gravitational constant.
3. Determine the Resultant Force:
Each mass experiences gravitational forces from the other two masses. By symmetry, the resultant force acting on any mass can be calculated. The angle between the forces acting on one mass due to the other two is 60∘. The net force Fnet can be calculated as:
Fnet=2F0cos(60∘2)=2F0cos(30∘)
Substituting cos(30∘)=√32:
Fnet=2⋅Gm2r2⋅√32=√3Gm2r2
4. Relate to Centripetal Force:
The net force acts as the centripetal force required for circular motion. If A is the radius of the circular path for the masses, we can equate the net force to the centripetal force:
Fnet=mω2A
where ω is the angular velocity.
5. Express Angular Velocity:
The angular velocity ω is related to the time period T by:
ω=2πT
Substituting this into the centripetal force equation gives:
Fnet=m(2πT)2A
6. Substituting and Rearranging:
Now substituting Fnet:
√3Gm2r2=m(2πT)2A
Canceling m from both sides:
√3Gmr2=(2πT)2A
7. Finding the Radius A:
The distance A from the centroid to a vertex of the triangle can be calculated as:
A=r√3
Substituting this back into the equation:
√3Gmr2=(2πT)2⋅r√3
8. Solving for Time Period T:
Rearranging gives:
T2=4π2r3√3Gm
Therefore, we find:
T∝r3/2m−1/2
Final Result:
The time period T of rotation is proportional to:
T∝r3/2m−1/2
We have three point masses m located at the corners of an equilateral triangle with side length r. The system rotates about the centroid of the triangle.
The gravitational force between any two masses m is given by:
F0=Gm2r2
where G is the gravitational constant.
Each mass experiences gravitational forces from the other two masses. By symmetry, the resultant force acting on any mass can be calculated. The angle between the forces acting on one mass due to the other two is 60∘. The net force Fnet can be calculated as:
Fnet=2F0cos(60∘2)=2F0cos(30∘)
Substituting cos(30∘)=√32:
Fnet=2⋅Gm2r2⋅√32=√3Gm2r2
The net force acts as the centripetal force required for circular motion. If A is the radius of the circular path for the masses, we can equate the net force to the centripetal force:
Fnet=mω2A
where ω is the angular velocity.
The angular velocity ω is related to the time period T by:
ω=2πT
Substituting this into the centripetal force equation gives:
Fnet=m(2πT)2A
Now substituting Fnet:
√3Gm2r2=m(2πT)2A
Canceling m from both sides:
√3Gmr2=(2πT)2A
The distance A from the centroid to a vertex of the triangle can be calculated as:
A=r√3
Substituting this back into the equation:
√3Gmr2=(2πT)2⋅r√3
Rearranging gives:
T2=4π2r3√3Gm
Therefore, we find:
T∝r3/2m−1/2
The time period T of rotation is proportional to:
T∝r3/2m−1/2
Similar Questions
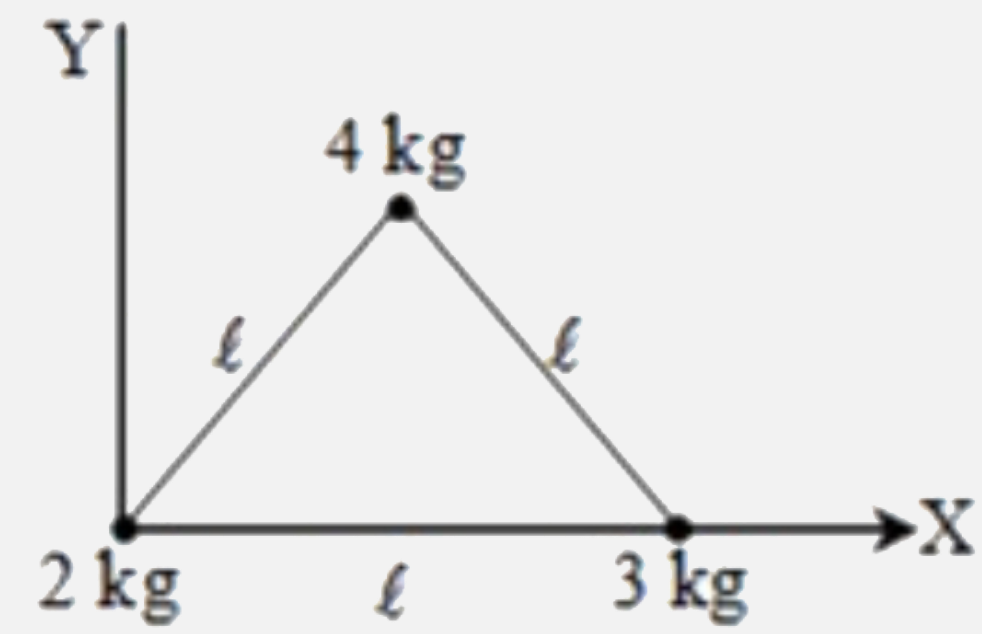
Three masses 2 kg , 3kg and 4kg are lying at the corners of an equilateral triangle of side I. The X coordinate of center of mass is
View SolutionThree point masses 'm' each are placed at the three vertices of an equilateral traingle of side 'a'. Find net gravitational force on any point mass.
View Solution
Knowledge Check
Three point masses each of mass m are placed at the corners of an equilateral triangle of side b. The moment of inertia of the system about an axis coinciding with one side of the triangle is
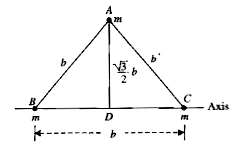 A3mb2Bmb2C(3/4)mb2D(2/3)mb2
A3mb2Bmb2C(3/4)mb2D(2/3)mb2
Three particle each of mass m are placed at the corners of equilateral triangle of side l

Which of the following is/are correct ?
View SolutionThree particles each of mass m are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is
View SolutionThree mass points each of mass m are placed at the vertices of an equilateral triangle of side 1. What is the gravitational field and potential due to the three masses at the centroid of the triangle ?
View SolutionThree mass points each of mass m are placed at the vertices of an equilateral tringale of side l. What is the gravitational field and potential due to three masses at the centroid of the triangle ?
View SolutionThree particle of mass m each are placed at the three corners of an equilateral triangle of side a. Find the work which should be done on this system to increase the sides of the triangle to 2a.
View SolutionThree particle of mass m each are placed at the three corners of an equilateral triangle of side a. Find the work which should be done on this system to increase the sides of the triangle to 2a.
View SolutionThree particle of mass m each are placed at the three corners of an equilateral triangle of side a. Find the work which should be done on this system to increase the sides of the triangle to 2a.
View Solution
