Can mass of a body be taken concentrated at its centre of mass for the purpose of calculating its rotational inertia ?
The correct Answer is:No
To determine whether the mass of a body can be taken as concentrated at its center of mass for the purpose of calculating its rotational inertia, we can analyze the concept of rotational inertia (or moment of inertia) in detail.
1. Understanding Moment of Inertia:
The moment of inertia (I) of a body is a measure of how difficult it is to change its rotational motion about an axis. It depends on the distribution of mass relative to the axis of rotation.
2. Definition of Center of Mass:
The center of mass of a body is the point at which the mass of the body can be considered to be concentrated for translational motion. However, for rotational motion, the distribution of mass around the axis of rotation is crucial.
3. Example of Different Shapes:
Consider two different shapes: a hollow sphere and a solid sphere. Both can have the same mass (m) and radius (r), and their centers of mass will coincide when they are positioned similarly.
4. Calculating Moment of Inertia:
- The moment of inertia of a hollow sphere about its center is given by:
Ihollow=23mr2
- The moment of inertia of a solid sphere about its center is given by:
Isolid=25mr2
5. Comparison of Moments of Inertia:
Although both spheres have the same mass and radius, their moments of inertia are different:
- Ihollow=23mr2
- Isolid=25mr2
6. Conclusion:
Since the moments of inertia are different despite having the same mass and center of mass, we conclude that the mass cannot simply be concentrated at the center of mass for the purpose of calculating rotational inertia. The distribution of mass relative to the axis of rotation is what determines the moment of inertia.
7. Final Statement:
Therefore, the statement that the mass of a body can be taken as concentrated at its center of mass for the purpose of calculating its rotational inertia is false.
The moment of inertia (I) of a body is a measure of how difficult it is to change its rotational motion about an axis. It depends on the distribution of mass relative to the axis of rotation.
The center of mass of a body is the point at which the mass of the body can be considered to be concentrated for translational motion. However, for rotational motion, the distribution of mass around the axis of rotation is crucial.
Consider two different shapes: a hollow sphere and a solid sphere. Both can have the same mass (m) and radius (r), and their centers of mass will coincide when they are positioned similarly.
- The moment of inertia of a hollow sphere about its center is given by:
Ihollow=23mr2
- The moment of inertia of a solid sphere about its center is given by:
Isolid=25mr2
Although both spheres have the same mass and radius, their moments of inertia are different:
- Ihollow=23mr2
- Isolid=25mr2
Since the moments of inertia are different despite having the same mass and center of mass, we conclude that the mass cannot simply be concentrated at the center of mass for the purpose of calculating rotational inertia. The distribution of mass relative to the axis of rotation is what determines the moment of inertia.
Therefore, the statement that the mass of a body can be taken as concentrated at its center of mass for the purpose of calculating its rotational inertia is false.
Similar Questions
The mass of a body cannot be considered to be concentrated at the centre of mass of the body for the purpose of computing its moment of inertia.
For then the moment of inertia of every body about an axis passing through its centre of mass would be zero.
View SolutionCalculate centre of mass of the system
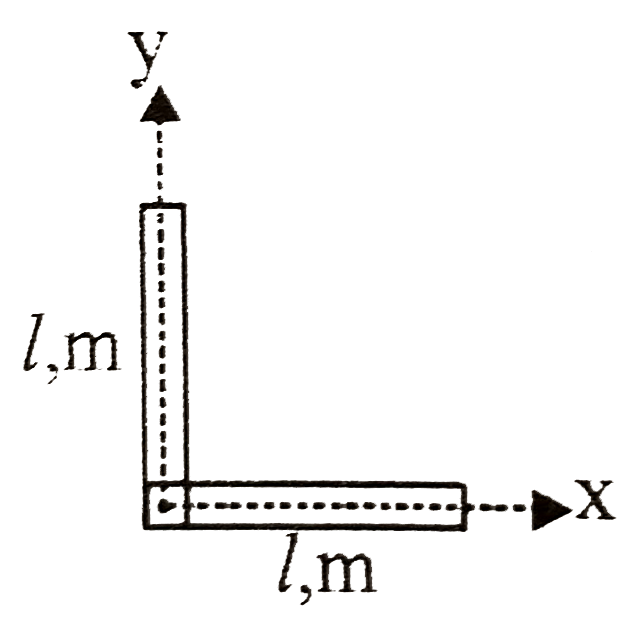
View Solution
Knowledge Check
The centre of mass of a body
Alies always at the geometrical centreBlies always inside the bodyClies always outside the bodyDmay lie within or outside the body(1) Centre of gravity (C.G.) of a body is the point at which the weight of the body acts,
(2) Centre of mass coincides with the centre of gravity if the earth is assumed to have infinitely large radius,
(3) To evaluate the gravitational field intensity due to any body at an external point, the entire mass of the body can be considered to be concentrated at its C.G..,
(4) The radius of gyration of any body rotating about an axis is the length of the perpendicular dropped from the C.G. of the body to the axis. which one of the following pairs of statements is correct ?A(1) and (4)B(1) and (2)C(1) and (3)D(3) and (4)Two thin discs each of mass M and radius r metre are attached to form a rigid body as shown in figure. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is
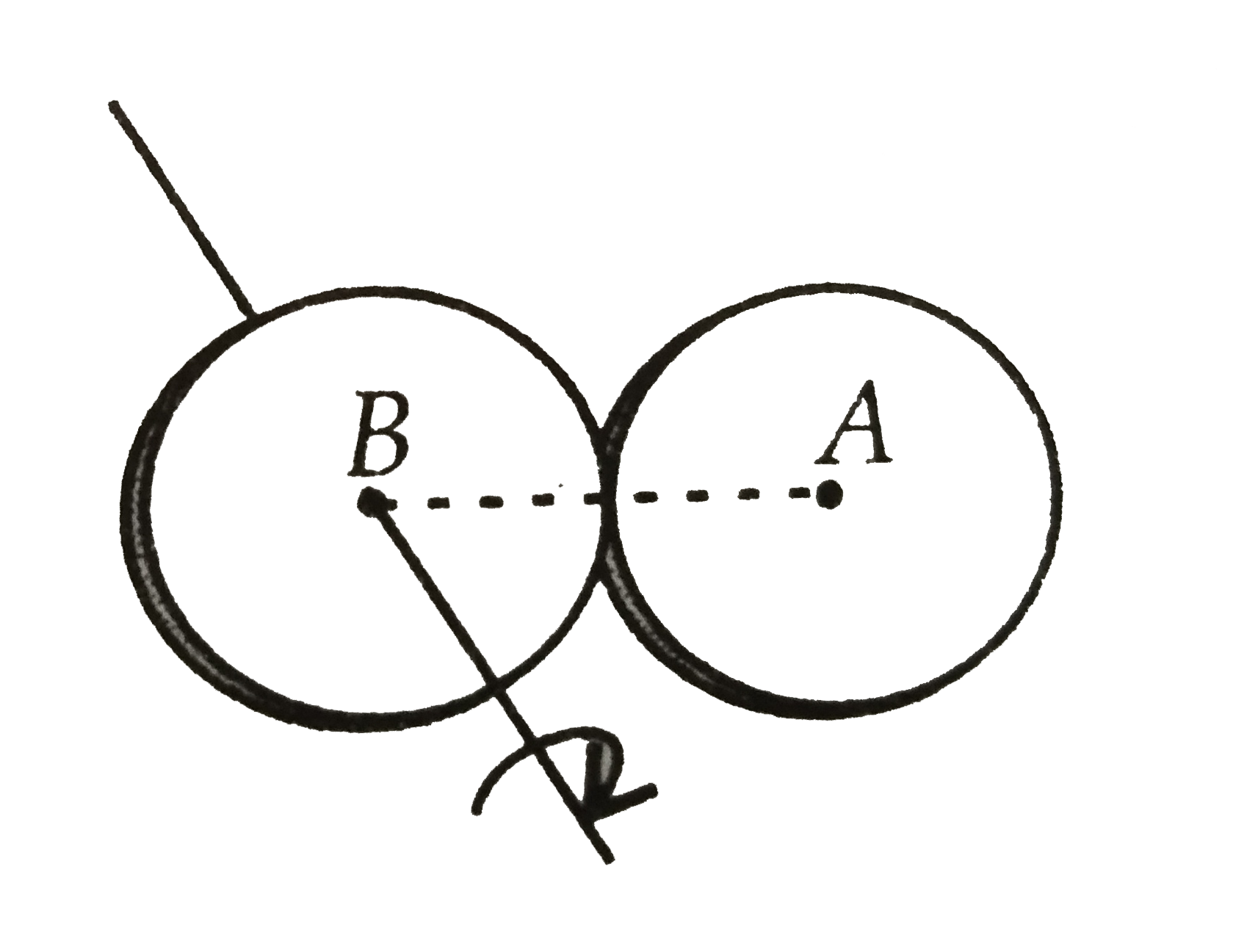 A2Mr2B3Mr2C4Mr2D5Mr2
A2Mr2B3Mr2C4Mr2D5Mr2
Mass of a body is 5 kg. What is its weight ?
View SolutionA semicircular lamina of mass m and radius r and centre C. Its center of mass is at a distance x from C. Its moment of inertia about an axis through its center of mass and perpendicular to its plane is:
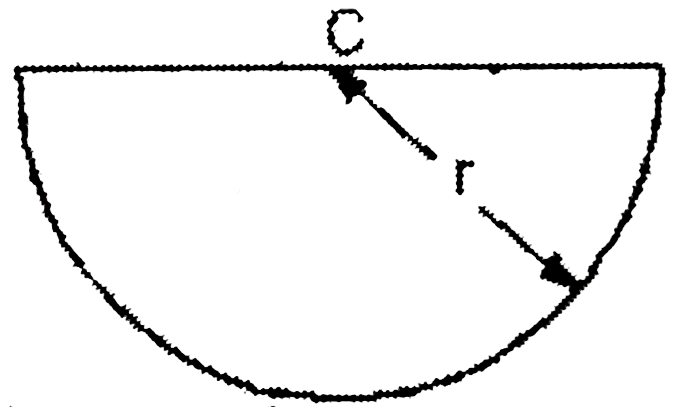
View SolutionCan the centre of mass of a body be at a point outside the body?
View SolutionRadius of gyration of a body about an axis at a distance 6 cm from its centre of mass is 10 cm. Find its radius of gyration about a parallel axis through its centre of mass.
View SolutionCircular disc of mass 2 kg and radius 1 m is rotating about an axis perpendicular to its plane and passing through its centre of mass with a rotational kinetic energy of 8 J. The angular momentum is (Js) is
View Solution
