A uniform rod AB which is free to swing in the vertical plane about a horizontal axis through A, is hanging freely. A particle of equal mass strikes the rod with a velocity v0 and gets stucks to it. Find the angular velocity of the combination immediately after the collision.
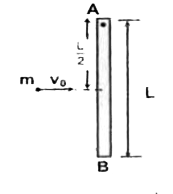
The correct Answer is:ω=6V07L (anticlockwise)
Step by step video & image solution for A uniform rod AB which is free to swing in the vertical plane about a horizontal axis through A, is hanging freely. A particle of equal mass strikes the rod with a velocity v_(0) and gets stucks to it. Find the angular velocity of the combination immediately after the collision. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A uniform rod of mass M and length L, which is free to rotate about a fixed vertical axis through O, is lying on a frictionless horizontal table. A particle of equal mass strikes the rod with a velocity V0 and sticks to it. The angular velocity of the combination immediately after the collision is:
View SolutionA wooden log of mass M and length L is hinged by a frictionless nail at O.A bullet of mass m strikes with velocity v and sticks to it. Find angular velocity of the system immediately after the collision aboutO.

View Solution
A uniform rod of length L is free to rotate in a vertical plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View Solution
A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
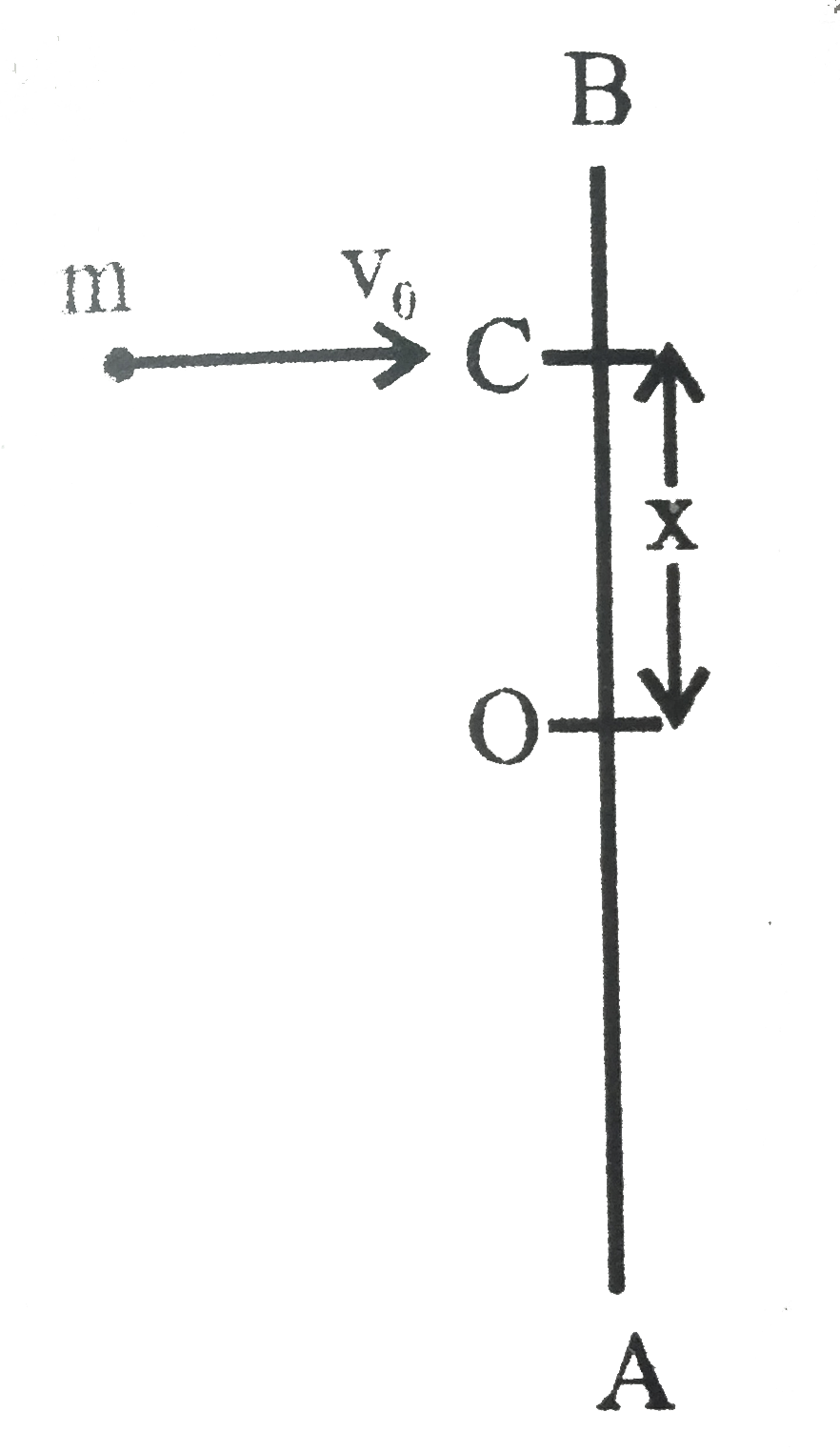
View SolutionA uniform rod AB of length L and mass M is lying on a smooth table. A small particle if mass m strike the rod with velocity v0 at point C at a distance comes to rest after collision. Then find the value of x, so that point A of the rod remains stationary just after collision.
 .
.
View Solution
A rod of length l forming an angle θ with the horizontal strikes a frictionless floor at A with its centre of mass velocity v0 and no angular velocity. Assuming that the impact at A is perfectly elastic. Find the angular velocity of the rod immediately after the impact.
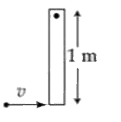
View SolutionA thin rod of mass 0.9 kg and length 1 m is suspended, at rest, from one end so that it can freely oscillate in the vertical plane. A particle of mass 0.1 kg moving in a straight line with velocity 80 m/s hits the rod at is bottom most point and sticks to it (see figure) . The angular speed ( in rad/s) of the rod immediately after the collision will be .
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

View SolutionA uniform rod AB of mass 3m and length 4l, which is free to turn in a vertical plane about a smooth horizontal axis through A, is released from rest when horizontal. When the rod first becomes vertical, a point C of the rod, where AC=3l strikes a fixed peg. Find the linear impulse exerted by the peg on the rod if
(a). The rod is brought to rest by the peg.
(b). The rod rebounds and next comes to instantaneous rest inclined to the downward vertical at an angle π3 radian.
View SolutionA L shaped rod of mass M is free to rotate in a vertical plane about axis A A as shown in figure. Maximum angular acceleration of rod is

View Solution