Three identical solid spheres (1, 2 and 3) are allowed to roll down from three inclined plane of angles $θ_{1}, θ_{2} and θ_{3}$ respectively starting at time t = 0, where $θ_{1} > θ_{2} > θ_{3}$ , then

sphere 1 will reach the bottom first

sphere 2 will reach the bottom first

sphere 3 will reach the bottom first

all the spheres will reach the bottom at the same time

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Answer

Step by step video & image solution for Three identical solid spheres (1, 2 and 3) are allowed to roll down from three inclined plane of angles theta_(1), theta_(2) and theta_(3) respectively starting at time t = 0, where theta_(1) gt theta_(2) gt theta_(3), then by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS ROTATIONAL MECHANICS

Similar Questions

If ${sin θ}_{1} + {sin θ}_{2} + {sin θ}_{3} = 3, t h e n {cos θ}_{1} + {cos θ}_{2} + {cos θ}_{3} =$
View Solution
If ${sin θ}_{1} + {sin θ}_{2} + {sin θ}_{3} = 3$ , then ${cos θ}_{1} + {cos θ}_{2} + {cos θ}_{3} =$
View Solution
A solid cylinder is rolling down a rough inclined plane of inclination $θ$ . Then
View Solution
Let $L_{1}, L_{2} and L_{3}$ be the three normals to the parabola $y^{2} = 4 a x$ from point P inclined at the angle $θ_{1}, θ_{2} and θ_{3}$ with x-axis, respectively. Then find the locus of point P given that $θ_{1} + θ_{2} + θ_{3} = α$ (constant).
View Solution
The net field $\to E$ due to the uniformly charged rod at $P$ makes angles $θ_{1}$ and $θ_{2}$ with $A P$ and $B P$ respectively. Then find the value of $θ_{1} / θ_{2}$

View Solution
The base of a triangle is divided into three equal parts. If $θ_{1}, θ_{2}, θ_{3}$ be thw angles subtended by these parts at the vertex, then prove that
$({cot θ}_{1} + {cot θ}_{2}) ({cot θ}_{2} + {cot θ}_{3}) = 4 cos e c^{2} θ_{2}$
View Solution
Let $\to a, \to b, \to c$ are three unit vector such that $\to a + \to b + \to c$ os also a unit vector. If pairwise angles between $\to a, \to b, \to c$ are $θ_{1}, θ_{2}$ and $θ_{3}$ respectively then ${cos θ}_{1} + {cos θ}_{2} + {cos θ}_{3}$ equals
View Solution
Two materials having coefficients of thermal conductivity '3k' and 'k' and thickness 'd' and '3d' respectively, are joined to form a slab as shown in the figures. The temperatures of the outer surfaces are $θ_{2}$ and $θ_{1}$ respectively $(θ_{2} > θ_{2})$ . The temperature at the interface is :

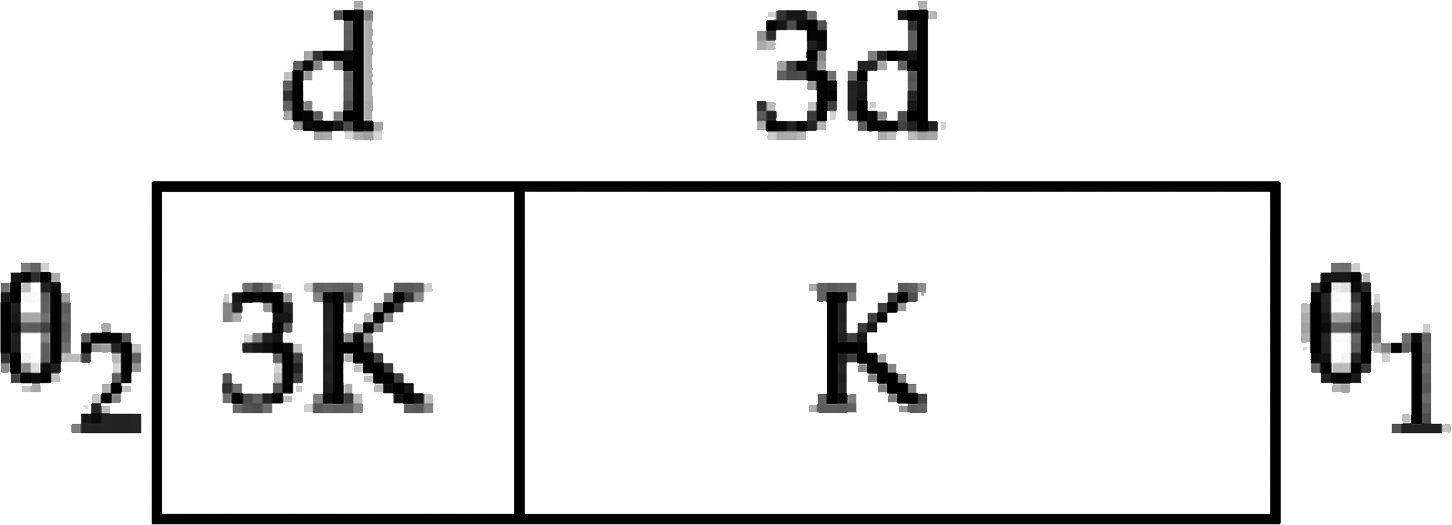
View Solution
If ${sin θ}_{1} + {sin θ}_{2} + {sin θ}_{3} = 3$ then find the value of ${cos θ}_{1} + {cos θ}_{2} + {cos θ}_{3} .$
View Solution
Two small spheres of masses $M_{1}$ and $M_{2}$ are suspended by weightless insulating threads of lengths $L_{1}$ and $L_{2}$ . The spheres carry charges $Q_{1}$ and $Q_{2}$ respectively. The spheres are suspended such that they are in level with one another and the threads are inclined to the vertical at angles $θ_{1}$ and $θ_{2}$ respectively . Which one of the following conditions is essential for $θ_{1} = θ_{2}$ ?
View Solution

Three identical solid spheres (1, 2 and 3) are allowed to roll down from three inclined plane of angles θ1,θ2andθ3 respectively starting at time t = 0, where θ1>θ2>θ3, then

The correct Answer is:A

Similar Questions

Recommended Questions

Three identical solid spheres (1, 2 and 3) are allowed to roll down from three inclined plane of angles $θ_{1}, θ_{2} and θ_{3}$ respectively starting at time t = 0, where $θ_{1} > θ_{2} > θ_{3}$ , then