A complex wave y=3sin2tcos500t is formed by superposition of how many waves?
The correct Answer is:3 waves
To solve the problem of how many waves are superimposed to form the complex wave y=3sin2tcos500t, we will break down the expression step by step.
1. Rewrite the Complex Wave:
The given wave equation is:
y=3sin2tcos500t
We can use the trigonometric identity for sin2t:
sin2t=1−cos2t2
Substituting this into the equation gives:
y=3(1−cos2t2)cos500t
2. Simplify the Expression:
Simplifying the equation further:
y=32(1−cos2t)cos500t
This can be expanded as:
y=32cos500t−32cos2tcos500t
3. Use the Product-to-Sum Formulas:
To simplify the term cos2tcos500t, we can use the product-to-sum identities:
cosAcosB=12(cos(A+B)+cos(A−B))
Here, A=2t and B=500t:
cos2tcos500t=12(cos(502t)+cos(498t))
Substituting this back into the equation gives:
y=32cos500t−34(cos(502t)+cos(498t))
4. Combine the Terms:
Now we can rewrite the equation:
y=32cos500t−34cos502t−34cos498t
5. Identify the Individual Waves:
The equation can now be seen as a superposition of three waves:
- 32cos500t
- −34cos502t
- −34cos498t
6. Count the Waves:
From the final expression, we can conclude that there are three distinct wave components in the superposition.
Final Answer:
The complex wave y=3sin2tcos500t is formed by the superposition of 3 waves.
---
The given wave equation is:
y=3sin2tcos500t
We can use the trigonometric identity for sin2t:
sin2t=1−cos2t2
Substituting this into the equation gives:
y=3(1−cos2t2)cos500t
Simplifying the equation further:
y=32(1−cos2t)cos500t
This can be expanded as:
y=32cos500t−32cos2tcos500t
To simplify the term cos2tcos500t, we can use the product-to-sum identities:
cosAcosB=12(cos(A+B)+cos(A−B))
Here, A=2t and B=500t:
cos2tcos500t=12(cos(502t)+cos(498t))
Substituting this back into the equation gives:
y=32cos500t−34(cos(502t)+cos(498t))
Now we can rewrite the equation:
y=32cos500t−34cos502t−34cos498t
The equation can now be seen as a superposition of three waves:
- 32cos500t
- −34cos502t
- −34cos498t
From the final expression, we can conclude that there are three distinct wave components in the superposition.
The complex wave y=3sin2tcos500t is formed by the superposition of 3 waves.
Similar Questions
If there are equations of two waves y=Asin(ωt−kx) and z=Asin(ωt−kx), then on superposition of the two waves, the amplitude of resultant wave is
View SolutionMany interesting wave phenomenon in nature cannot just be described by a single wave, instead one must analyze complex wave forms in terms of a combinations of many travelling waves. To analyze such wave combinations, we make use of the principle of superposition which states that if two or more travelling waves are moving through a medium and combine at a given point, the resultant displacement of the medium at that point is sum of the displacement of individual waves. Two pulses travelling on the same string are described by
y1=5(3x−4t)2+2 and y2=−5(3x+4t−6)2+2
The time when the two waves cancel everywhere
View Solution
Knowledge Check
The stationary wave y = 2a sinkx cosωt in a stretched string is the result of superposition of y1=asin(kx−ωt) and
Ay2=acos(kx+ωt)By2=asin(kx+ωt)Cy2=acos(kx−ωt)Dy2=asin(kx−ωt)
Many interesting wave phenomenon in nature cannot just be described by a single wave, instead one must analyze complex wave forms in terms of a combinations of many travelling waves. To analyze such wave combinations, we make use of the principle of superposition which states that if two or more travelling waves are moving through a medium and combine at a given point, the resultant displacement of the medium at that point is sum of the displacement of individual waves. Two pulses travelling on the same string are described by
y1=5(3x−4t)2+2 and y2=−5(3x+4t−6)2+2
The point where the two waves always cancel
View SolutionMany interesting wave phenomenon in nature cannot just be described by a single wave, instead one must analyze complex wave forms in terms of a combinations of many travelling waves. To analyze such wave combinations, we make use of the principle of superposition which states that if two or more travelling waves are moving through a medium and combine at a given point, the resultant displacement of the medium at that point is sum of the displacement of individual waves. Two pulses travelling on the same string are described by
y1=5(3x−4t)2+2 and y2=−5(3x+4t−6)2+2
The direction in which each pulse is travelling
View SolutionConsider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
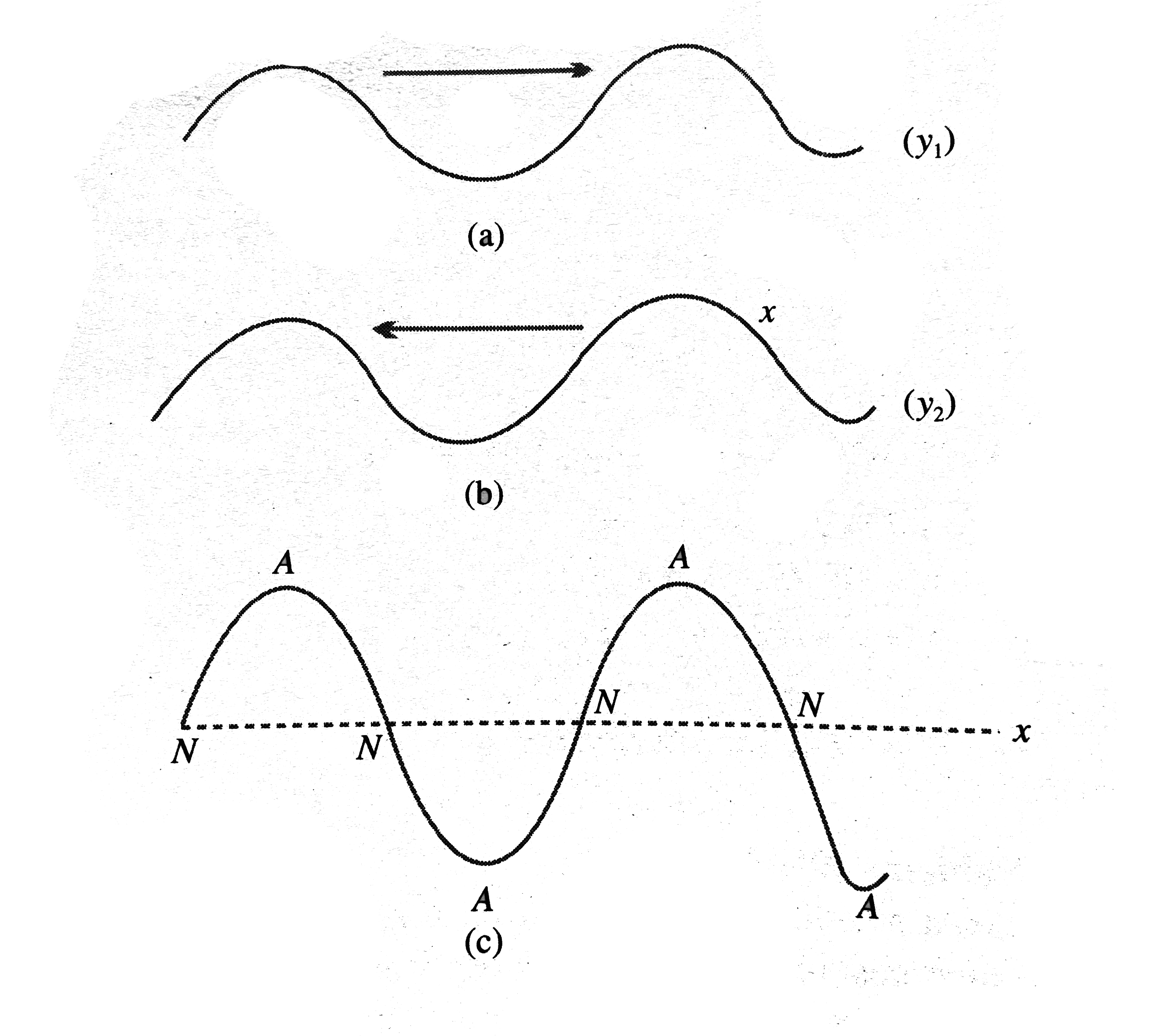
Figure 7.104( c) shows the standing wave pattern at t=0 due to superposition of waves given by y1 and y2 in Figs.7.104(a) and (b) . In Fig. 7.104 (c ) , N is a node and A and antinode . At this instant say t=0 , instantaneous velocity of points on the string named as A
View SolutionFour sound sources produce the following four waves
(i) y1=asin(ωt+ϕ1)
(ii) y2=asin2ωt
(iii) y3=a'sin(ωt+ϕ2)
(iv) y4=a'sin(3ωt+ϕ)
Superposition of which two waves gives rise to interference?
View SolutionThe stationary wave y = 2a sin kx cosωt in a closed organ pipe is the result of the superposition of y = a sin( ωt — kx) and
View SolutionThe equation of a stationary wave is y=0.8cos(πx20)sin200πt where x is in cm and t is in s. The separation between consecutive nodes will be
View SolutionThe displacement of two interfering light waves are y1=4sinωt and y2=3cos(ωt). The amplitude of the resultant waves is (y1 and y2 are in CGS system)
View Solution
