The frequency of a tuning fork with an amplitude A = 1 cm is 250 Hz. The maximum velocity of any particle in air is equal to
2.5 m/s
5π m/s
(3.30/π) m/sec
none of these
The correct Answer is:B
To find the maximum velocity of any particle in air when a tuning fork is vibrating, we can use the relationship between amplitude, frequency, and maximum velocity in simple harmonic motion.
1. Identify the Given Values:
- Amplitude (A) = 1 cm = 0.01 m (convert centimeters to meters)
- Frequency (f) = 250 Hz
2. Calculate Angular Frequency (ω):
- The angular frequency (ω) is given by the formula:
ω=2πf
- Substituting the value of frequency:
ω=2π×250 Hz
- Calculate:
ω=500π rad/s
3. Calculate Maximum Velocity (v_max):
- The maximum velocity (v_max) of a particle in simple harmonic motion is given by:
vmax=ω×A
- Substituting the values of ω and A:
vmax=(500π)×(0.01) m
- Calculate:
vmax=5π m/s
4. Final Answer:
- Therefore, the maximum velocity of any particle in air is:
vmax=5π m/s
- Amplitude (A) = 1 cm = 0.01 m (convert centimeters to meters)
- Frequency (f) = 250 Hz
- The angular frequency (ω) is given by the formula:
ω=2πf
- Substituting the value of frequency:
ω=2π×250 Hz
- Calculate:
ω=500π rad/s
- The maximum velocity (v_max) of a particle in simple harmonic motion is given by:
vmax=ω×A
- Substituting the values of ω and A:
vmax=(500π)×(0.01) m
- Calculate:
vmax=5π m/s
- Therefore, the maximum velocity of any particle in air is:
vmax=5π m/s
Similar Questions
Knowledge Check
The frequency of tuning fork is 256 Hz. It will not resonate with a fork of frequency
A768 HzB738 HzC512 HzD256 Hz
The frequency of a tuning fork is 150 Hz and distance travelled by the sound, produced in air is 20 cm in one vibration. Calculate the speed of sound in air.
View SolutionA stationary observer receives sound waves from two tuning forks, one of which approaches and the other recedes with the same velocity. As this takes place, the observer hears beats of frequency υ=2Hz. Find the velocity of each tuning fork if their oscillation frequency is υ0=680Hz and the velocity of sound in air is υs=340ms.
View SolutionIn determination of velocity of sound in air using resonance column tube, radius of cylindrical tube is 1 cm and frequency of tuning fork is 256 Hz. If velocity of sound is 340 m/s then length of air column in the tube when first resonance occurs, is
View SolutionThe frequency of tuning forks A and B are respectively 5% more and 4% less than the frequency of tuning fork C. When A and B are simultaneously excited, 9 beats per second are produced. Then the frequency of the tuning fork A (in Hz) is
View SolutionThere is a source of sound (a tuning fork) moving towards a reflecting wall will a speed of 30ms−1. The velocity of the sound in air is 330ms−1and the frequency of the tuning fork is 600 Hz. The observer is between the source and the wall and is moving with some velocity V1 towards the wall. The beat frequency heard by the observer is 4 Hz. If the tuning fork is waxed, the frequency beats heard by the observer becomes 3 Hz. If the new frequency of tuning fork is k then k/50 is
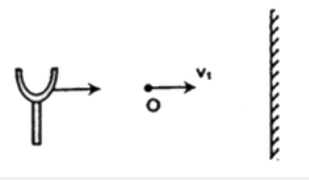
View SolutionThe frequency of tuning forks A and B are respectively 3% more and 2% less than the frequency of tuning fork C. When A and B are simultaneously excited, 5 beats per second are produced. Then the frequency of the tuning fork A (in Hz) Is
View SolutionThe natural frequency of an air column in a pipe fixed at one end, of length 17 cm is 500 Hz. At what length of air column, a tuning fork of frequency 250 Hz will resonate with it?
View Solution
