In a 10 m high room a partition of height 7m separates two students on either side. Both light and sound waves can deviate from their path if they experience any obstruction. Then why is it that the two students can converse with each other even if one cannot see the other?
The correct Answer is:The size of partition is very large as compared to the wavelength of light and hence it is not diffracted and both students cannot see each other. The wavelength of sound waves is of the order of height of partition. It causes sound to diffraction and they can converse with each other.
Step-by-Step Solution:
1. Understanding the Setup: We have a room that is 10 meters high, with a partition that is 7 meters high. This creates a gap of 3 meters between the top of the partition and the ceiling of the room.
2. Identifying the Waves: The two types of waves we are considering are light waves and sound waves. Both can be obstructed by the partition, but they behave differently when encountering the gap.
3. Concept of Diffraction: Diffraction is the phenomenon where waves bend around obstacles or spread out after passing through small openings (slits). The ability of a wave to diffract depends on the relationship between the size of the opening and the wavelength of the wave.
4. Wavelength Comparison:
- The wavelength of light is much smaller than the gap size (3 meters), which is not comparable.
- The wavelength of sound is much larger and is comparable to the gap size.
5. Application of Diffraction:
- Since the gap (3 meters) is comparable to the wavelength of sound, sound waves can diffract through the gap and reach the other student.
- Light waves, on the other hand, do not diffract significantly because their wavelength is much smaller than the gap size, and thus they cannot bend around the partition.
6. Conclusion: The two students can converse because sound waves can diffract through the gap created by the partition and the ceiling, while light waves cannot. Therefore, even though one student cannot see the other, they can still communicate through sound.
Final Answer: The two students can converse because sound waves can diffract through the 3-meter gap above the partition, while light waves cannot due to their much smaller wavelength compared to the gap size.
---
- The wavelength of light is much smaller than the gap size (3 meters), which is not comparable.
- The wavelength of sound is much larger and is comparable to the gap size.
- Since the gap (3 meters) is comparable to the wavelength of sound, sound waves can diffract through the gap and reach the other student.
- Light waves, on the other hand, do not diffract significantly because their wavelength is much smaller than the gap size, and thus they cannot bend around the partition.
Similar Questions
Two identical speakers emit sound waves of frequency 680HZ uniformly in all directions with a total audio output of 1mW each. The speed of sound in air is 340m/s. A point P is a distance 2.00m from one speaker and 3.00m from the other.
(a) Finf the intensity I1 and I2 from rach speaker at point p separately.
(b) If the speakers are driven coherently and in phase, what is the intensity at point p?
(c ) If they driven coherently but of phase by 180∘, what is the intensity at point P?
(d) If the speakers are incoherent, what is the intensity at point p?
View SolutionTwo identical copper spheres are separated by 1m in vacuum. How many electrons would have to be removed from one sphere and added to the other so that they now attract each other with a force of 0.9N?
View Solution
Knowledge Check
Light from sodium lamp is made to pass through two polaroids placed one after the other in the path of light. Taking the intensity of the incident light as 100%, the intensity of the out coming light that can be varied in the range
A0% to 100%B0% to 50%C0% to 25%D0% to 75%
two trains move towards each other sith the same speed. The speed of sound is 340 m/s. If the height of the tone of the whistle of one of them heard on the other changes 9/8 times, then the speed of each train should be
View SolutionTwo canoes are 10 m apart on a lake. Each bobs up and down with a period of 4.0 s. when one canoe is at its highest point, the other canoe is at its lowest point. Both canoes are always within a single cycle of the waves determine the speed of the wave.
View SolutionA metallic rod of length 1m is rigidly clamped at its mid point. Longirudinal stationary wave are setup in the rod in such a way that there are two nodes on either side of the midpoint. The amplitude of an antinode is 2×10−6m. Write the equation of motion of a point 2 cm from the midpoint and those of the constituent waves in the rod, (Young,s modulus of the material of the rod =2×1011Nm−2 , density =8000kg−m−3). Both ends are free.
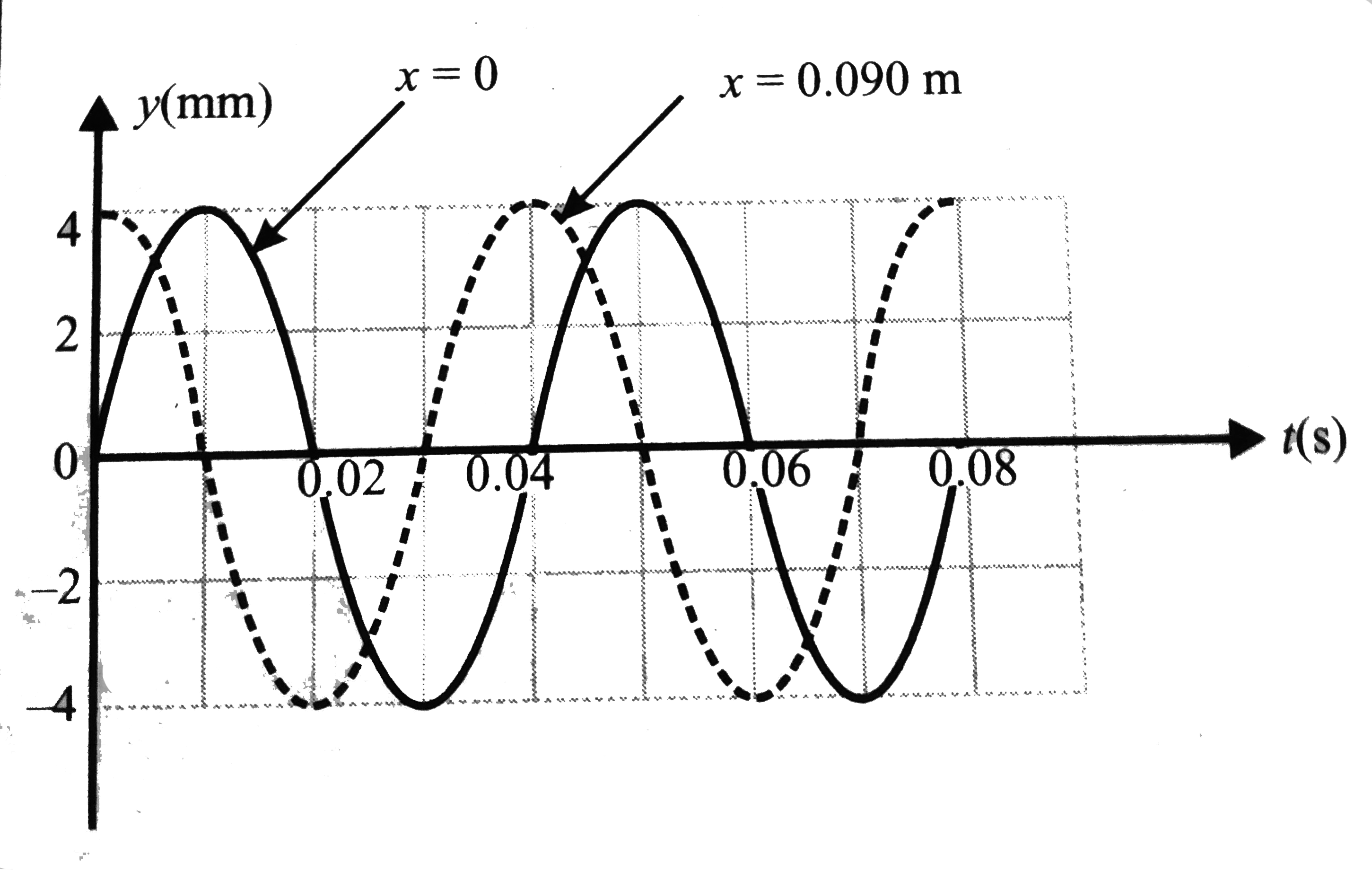
View SolutionA sinusoidal wave is propagating along a streched string that lies along the x-axis. The displacement of the string as a function of time is graphed in for particles at x-0 and at x=0.0900 m. (a) what is the amplitude of the wave? (b)what is the period of the wave? (c ) you are told that the two points x=0 and x=0.0900 m are within one wavelength of each other. if the wave is moving in the +x-direction, determine the wavelength and the wave speed. (d) if instead the wave is moving in the -x-direction, determine the wavelength and the wave speed. (e) would it be possible to derermine definitely the wavelength in parts (c ) and (d) if you were not told that the two points were within one wavelength of each other? why ot why not?
View SolutionA man sitting at a height of 20m on a tall tree on a small island in the middle of a river observes two poles directly opposite to each other on the two banks of the river and in line with the foot of tree. If the angles of depression of the feet of the poles from a point at which the man is sitting on the tree on either side of the river are 600and300 respectively. Find the width of the river.
View SolutionThere are eight rooms on the first floor of a hotel, with four rooms on each side of the corridor, symmetrically situated (that is each room is exactly opposite to one other room). Four guests have to be accommodated in four of the eight rooms (that is, one in each) such that no two guests are in adjacent rooms or in opposite rooms. in how many ways can the guests be accommodated?
View SolutionTwo vertical poles of height 10 m and 40 m stand apart on a horizontal plane. The height (in meters) of the point of intersection of the line joining the top of each pole to the foot of the other, from this horizontal plane is
View Solution
