In Young's double slit experiment the 7th maximum with wavelength λ1is at a distance d1, and that with wavelength λ2 is at distance d2. Then d1/d2 is
λ1λ2
λ2√λ1
λ21/λ22
λ22/λ12
The correct Answer is:A
To solve the problem, we need to analyze the relationship between the distances of the maxima in Young's double slit experiment for two different wavelengths. Here's the step-by-step solution:
Step 1: Understand the conditions for maxima in Young's double slit experiment
In Young's double slit experiment, the condition for maxima is given by the formula:
Δx=nλ
where Δx is the path difference, n is the order of the maximum (an integer), and λ is the wavelength of the light used.
Step 2: Relate the path difference to the distance from the central maximum
The path difference can also be expressed in terms of the angle θ and the distance d between the slits:
dsinθ=nλ
For small angles, we can use the approximation sinθ≈tanθ≈yD, where y is the distance from the central maximum to the n-th maximum and D is the distance from the slits to the screen.
Step 3: Express the distance y for the n-th maximum
From the above relationships, we can express y as:
y=nλDd
This means that the distance to the n-th maximum is directly proportional to the wavelength.
Step 4: Apply the formula for both wavelengths
For the 7th maximum with wavelength λ1:
d1=7λ1Dd
For the 7th maximum with wavelength λ2:
d2=7λ2Dd
Step 5: Find the ratio d1d2
Now, we can find the ratio of the distances:
d1d2=7λ1Dd7λ2Dd=λ1λ2
Conclusion
Thus, the ratio of the distances d1d2 is given by:
d1d2=λ1λ2
In Young's double slit experiment, the condition for maxima is given by the formula:
Δx=nλ
where Δx is the path difference, n is the order of the maximum (an integer), and λ is the wavelength of the light used.
The path difference can also be expressed in terms of the angle θ and the distance d between the slits:
dsinθ=nλ
For small angles, we can use the approximation sinθ≈tanθ≈yD, where y is the distance from the central maximum to the n-th maximum and D is the distance from the slits to the screen.
From the above relationships, we can express y as:
y=nλDd
This means that the distance to the n-th maximum is directly proportional to the wavelength.
For the 7th maximum with wavelength λ1:
d1=7λ1Dd
For the 7th maximum with wavelength λ2:
d2=7λ2Dd
Now, we can find the ratio of the distances:
d1d2=7λ1Dd7λ2Dd=λ1λ2
Thus, the ratio of the distances d1d2 is given by:
d1d2=λ1λ2
Similar Questions
If an interference experiment is performed using two wavelengths close to each other, two interference patterns corresponding to the two wavelengths are obtained on the screen. The frings system remains distinct up to a point on the screen where the nth order maximum of one wavelength falls on the nth order minimum of the other wavelength. Suppose in Young's double sit experiment, sodium light composed of two wavelengths λ1andλ2 close to each other (with λ2 greater than λ1) is used. The order n, up to which the fringes can be seen on the screen, is given by
View SolutionDraw a neat labelled diagram of Young.s Double Slit experiment. Show that β=λDd, where the terms have their usual meaning (either for bright or dark fringe).
View Solution
Knowledge Check
In Young's double slit experiment, the 10th maximum of wavelength λ1 is at a distance y1 from its central maximum and the 5th maximum of wavelength λ2 is at a distance y2 from its central maximum. The ratio y1/y2 will be
A2λ1λ2B2λ2λ1Cλ12λ2Dλ22λ1In a Young's double slit experiment, (slit distance d) monochromatic light of wavelength λ is used and the fringe pattern observed at a distance D from the slits. The angular position of the bright fringes are
Asin−1(Nλd)Bsin−1⎛⎜ ⎜⎝(N+12)λd⎞⎟ ⎟⎠Csin−1(NλD)Dsin−1⎛⎜ ⎜⎝(N+12)λD⎞⎟ ⎟⎠
In a young's doule slits experiment, a monochromatic source of wavelength λ is used to illuminate the two slits
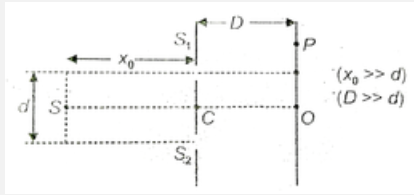
S1 and S2. The slitss S1 and S2 are identical and source S is placed symmetrically as shown. interference pattern is observed on a screen at a distance D from the centre of slit. The distance between the slits is d.
If the size of slits S1 is slightly decreased, then
View SolutionIn a young's doule slits experiment, a monochromatic source of wavelength λ is used to illuminate the two slits
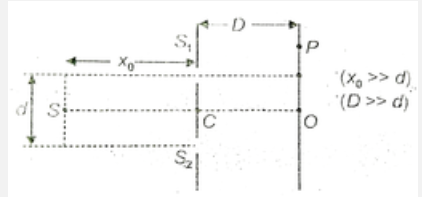
S1 and S2. The slitss S1 and S2 are identical and source S is placed symmetrically as shown. interference pattern is observed on a screen at a distance D from the centre of slit. The distance between the slits is d.
If the resultant intensity at P is same as that O, then the distance OP can not be
View SolutionIn a young's doule slits experiment, a monochromatic source of wavelength λ is used to illuminate the two slits

S1 and S2. The slitss S1 and S2 are identical and source S is placed symmetrically as shown. interference pattern is observed on a screen at a distance D from the centre of slit. The distance between the slits is d.
If the source is moved up by a very small distance y0, the central maxima will shift
View SolutionIn young's double slit experiment the separation d between the slits is 2mm, the wavelength λ of the light used is 5896Å and distance D between the screen and slits is 100cm. It is found that the angular width of the fringes is 0.20∘. To increases the fringe angular width to 0.21∘(with same λ and D) the separtion between the slits needs to be changed to
View SolutionIn the figure an arrangement of young's double slit experiment is shown. A parallel beam of light of wavelength 'λ' (in medium n1) is incident at an angle 'θ' as shown. Distance S1O=S2O. Point 'O' is the origin of the coordinate system. The medium on the left and right side of the plane of slits has refractive index n1 and n2 respectively. Distance between the slits is d. The distance between the screen and the plane of slits is D.
Using D=1m,d=1mm,θ=30∘,λ=0.3mm,n1=43,n2=109, answer the following
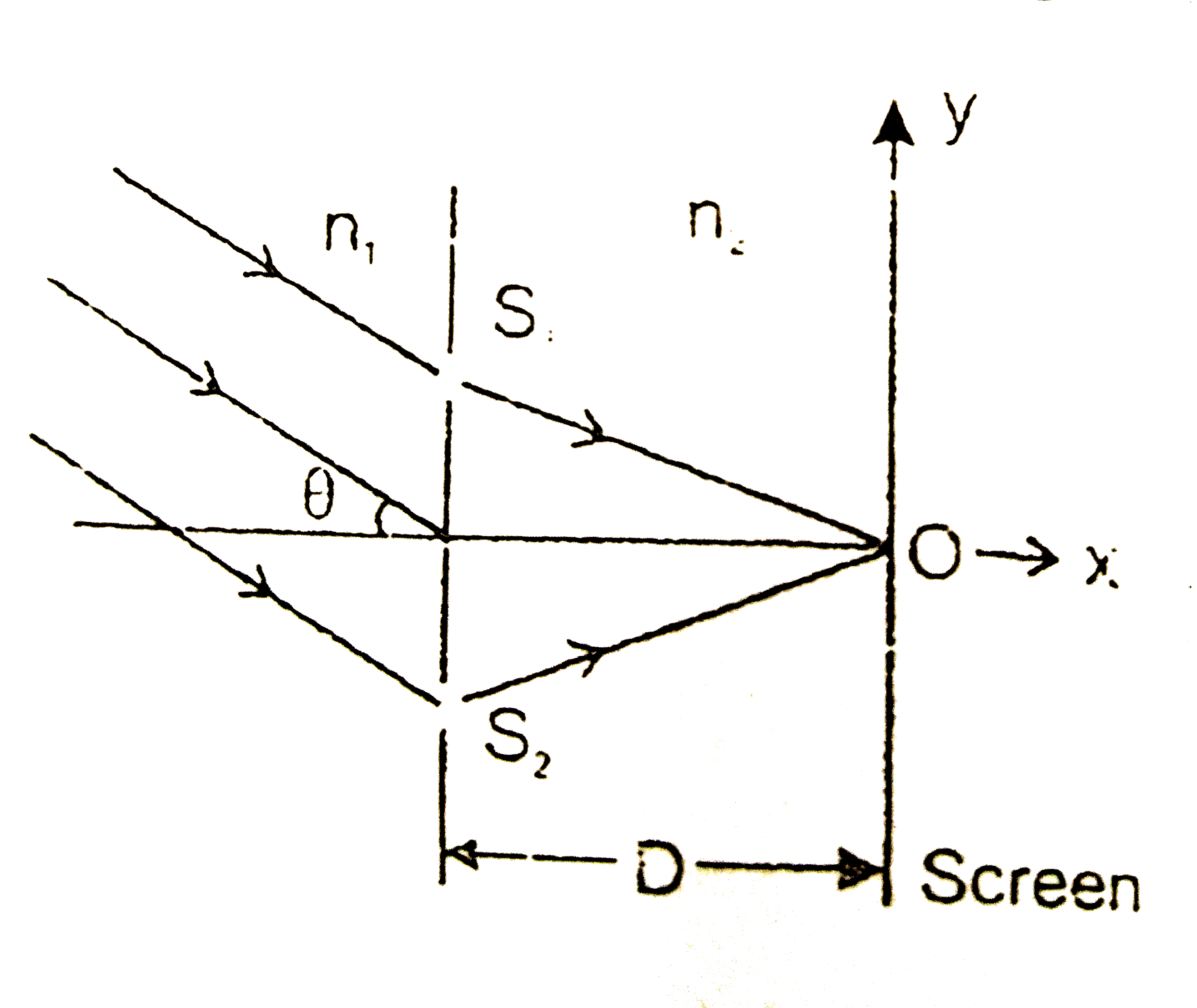
They-corrdinate of the point where the total phase difference between the interefering waves is zero, is
View SolutionIn the figure an arrangement of young's double slit experiment is shown. A parallel beam of light of wavelength 'λ' (in medium n1) is incident at an angle 'θ' as shown. Distance S1O=S2O. Point 'O' is the origin of the coordinate system. The medium on the left and right side of the plane of slits has refractive index n1 and n2 respectively. Distance between the slits is d. The distance between the screen and the plane of slits is D.
Using D=1m,d=1mm,θ=30∘,λ=0.3mm,n1=43,n2=109, answer the following

If the intensity due to each light wave at point 'O' is I0 then the resultant intensity at point 'O' will be -
View Solution
