Current in LCR ac circuit will be maximum when omega is
as large as possible
√LC
√1LC
√LCR
The correct Answer is:C
To determine the condition under which the current in an LCR AC circuit is maximum, we can follow these steps:
1. Understand the relationship of current in LCR circuit:
The current I in an LCR circuit can be expressed as:
I=VZ
where Z is the impedance of the circuit.
2. Impedance expression:
The impedance Z for a series LCR circuit is given by:
Z=√R2+(XL−XC)2
where XL=ωL (inductive reactance) and XC=1ωC (capacitive reactance).
3. Maximizing the current:
To maximize the current I, we need to minimize the impedance Z. This means we need to minimize the term (XL−XC).
4. Condition for minimum impedance:
The term (XL−XC) will be zero when:
XL=XC
Therefore, we set:
ωL=1ωC
5. Solving for ω:
Rearranging the equation ωL=1ωC gives:
ω2=1LC
Taking the square root of both sides results in:
ω=1√LC
6. Conclusion:
The current in the LCR AC circuit will be maximum when:
ω=1√LC
This frequency is known as the resonance frequency.
The current I in an LCR circuit can be expressed as:
I=VZ
where Z is the impedance of the circuit.
The impedance Z for a series LCR circuit is given by:
Z=√R2+(XL−XC)2
where XL=ωL (inductive reactance) and XC=1ωC (capacitive reactance).
To maximize the current I, we need to minimize the impedance Z. This means we need to minimize the term (XL−XC).
The term (XL−XC) will be zero when:
XL=XC
Therefore, we set:
ωL=1ωC
Rearranging the equation ωL=1ωC gives:
ω2=1LC
Taking the square root of both sides results in:
ω=1√LC
The current in the LCR AC circuit will be maximum when:
ω=1√LC
This frequency is known as the resonance frequency.
Similar Questions
An AC circuit consists of an inductor of inductance 0.5H and a capacitor of capacitance 8μF in series. The current in the circuit is maximum when the angular frequency of AC source is
View SolutionCurrent in an ac circuit is given by I=3sinωt+4cosωt, then
View SolutionAnswer the following:
(a) What do you understand by 'sharpness of resonance' for a series LCR resonant circuit? How is it related with the quality factor 'Q' of the circuit? Using the graphs given in the diagram, explain the factors which affect it. For which graph is the resistance (R ) minimum?
(b) A 2μF capacitor, 100Ω resistor and 8H inductor are connected in series with an ac source. Find the frequency of the ac source for which the current drawn in the circuit is maximum.
If the peak value of emf of the source is 200 V, calculate the (i) maximum current, and (ii) inductive and capacitive reactance of the circuit at resonance.
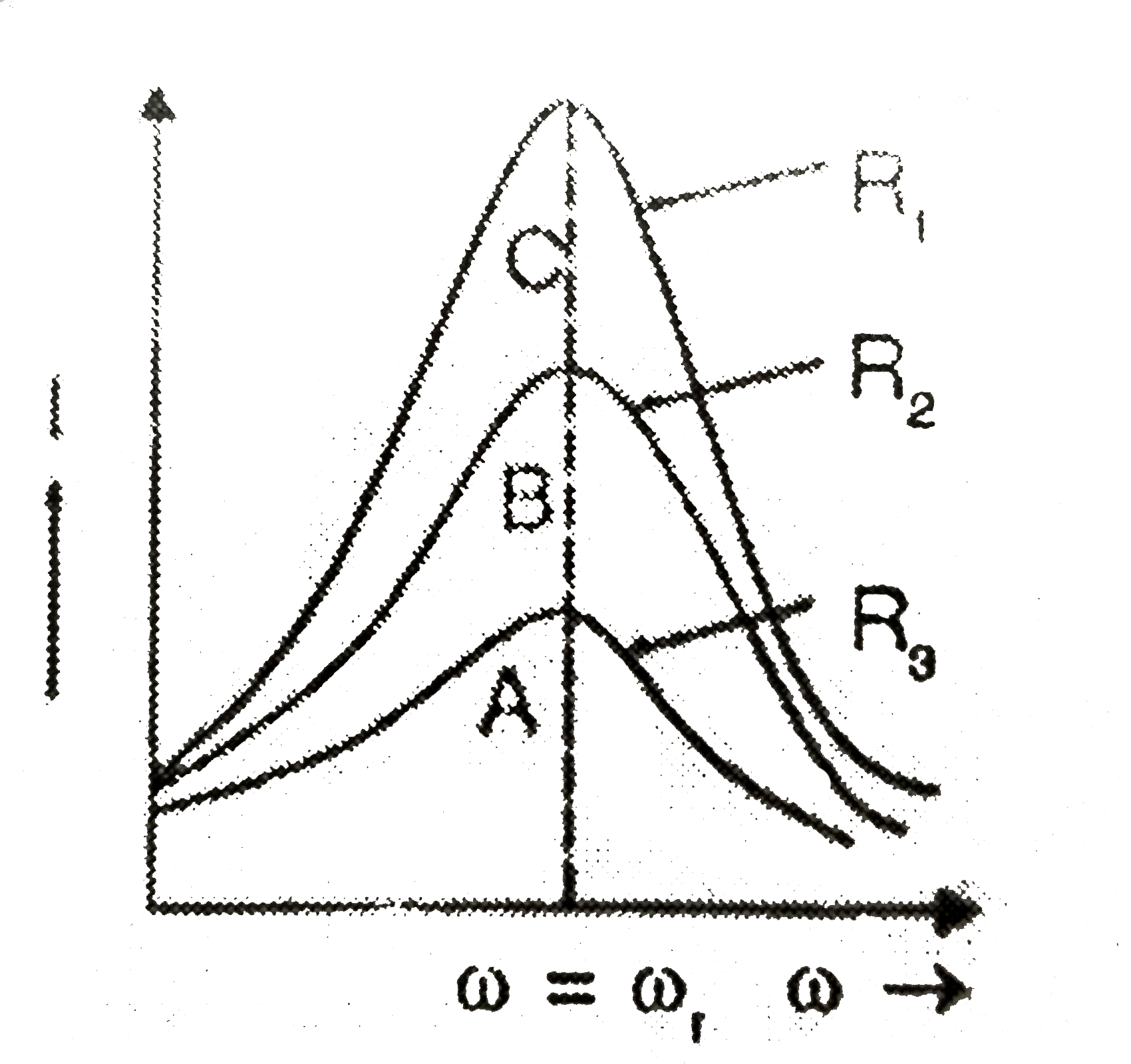
View SolutionStatement 1: In the purely resistive element of a series LCR, ac circuit the maximum value of rms current increase with increase in the angular frequency of the applied emf.
Statement 2: Imax=εmaxZ,Z= ⎷R2+(ωL−1(ωC)2),
where (Imax) is the peak current in a cycle.
View SolutionAssertion : Angular frequency of LC oscillations is 2rad/s and maximum current in the circuit is 1A. Then, maximum rate of change of current should be 2A/s.
Reason: (dIdt)max=(Imax)ω
View SolutionIn an ac circuit the current
View SolutionThe emf and current in a circuit are such that E=E0sinωt and I=I0sin(ωt−θ). This AC circuit contains
View SolutionWhat is the value of inductance L for which the current is maximum in a series LCR circuit with C=10μFandω=1000s−1 ?
View SolutionThe average power dissipated in AC circuit is 2W. If a current flowing throuh a circuit is 2A, impedance is 1Ω, then what is the power factor of the circuit?
View SolutionA 100μF capacitor in series with a 40Ω resistance is connected to 110 V, 60 Hz supply.
(a) what is the maximum current in the circuit ?
(b) what is the time lag between the current maximum and the voltage maximum ?
View Solution
