The value of 1+(1+i)+(1+i2)+(1+i3)=
To solve the expression 1+(1+i)+(1+i2)+(1+i3), we will break it down step by step.
Step 1: Write down the expression
We start with the expression:
1+(1+i)+(1+i2)+(1+i3)
Step 2: Simplify the expression
We can rewrite the expression by distributing:
=1+1+i+1+i2+1+i3
Combining the constant terms, we have:
=4+i+i2+i3
Step 3: Substitute the values of i2 and i3
We know that:
- i2=−1
- i3=i⋅i2=i⋅(−1)=−i
Substituting these values into the expression:
=4+i−1−i
Step 4: Combine like terms
Now, we can combine the terms:
=(4−1)+(i−i)=3+0=3
Final Answer
Thus, the value of the expression 1+(1+i)+(1+i2)+(1+i3) is:
3
We start with the expression:
1+(1+i)+(1+i2)+(1+i3)
We can rewrite the expression by distributing:
=1+1+i+1+i2+1+i3
Combining the constant terms, we have:
=4+i+i2+i3
We know that:
- i2=−1
- i3=i⋅i2=i⋅(−1)=−i
=4+i−1−i
Now, we can combine the terms:
=(4−1)+(i−i)=3+0=3
Thus, the value of the expression 1+(1+i)+(1+i2)+(1+i3) is:
3
Similar Questions
Knowledge Check
In the circuit shown, the value of currents I1,I2andI3 are
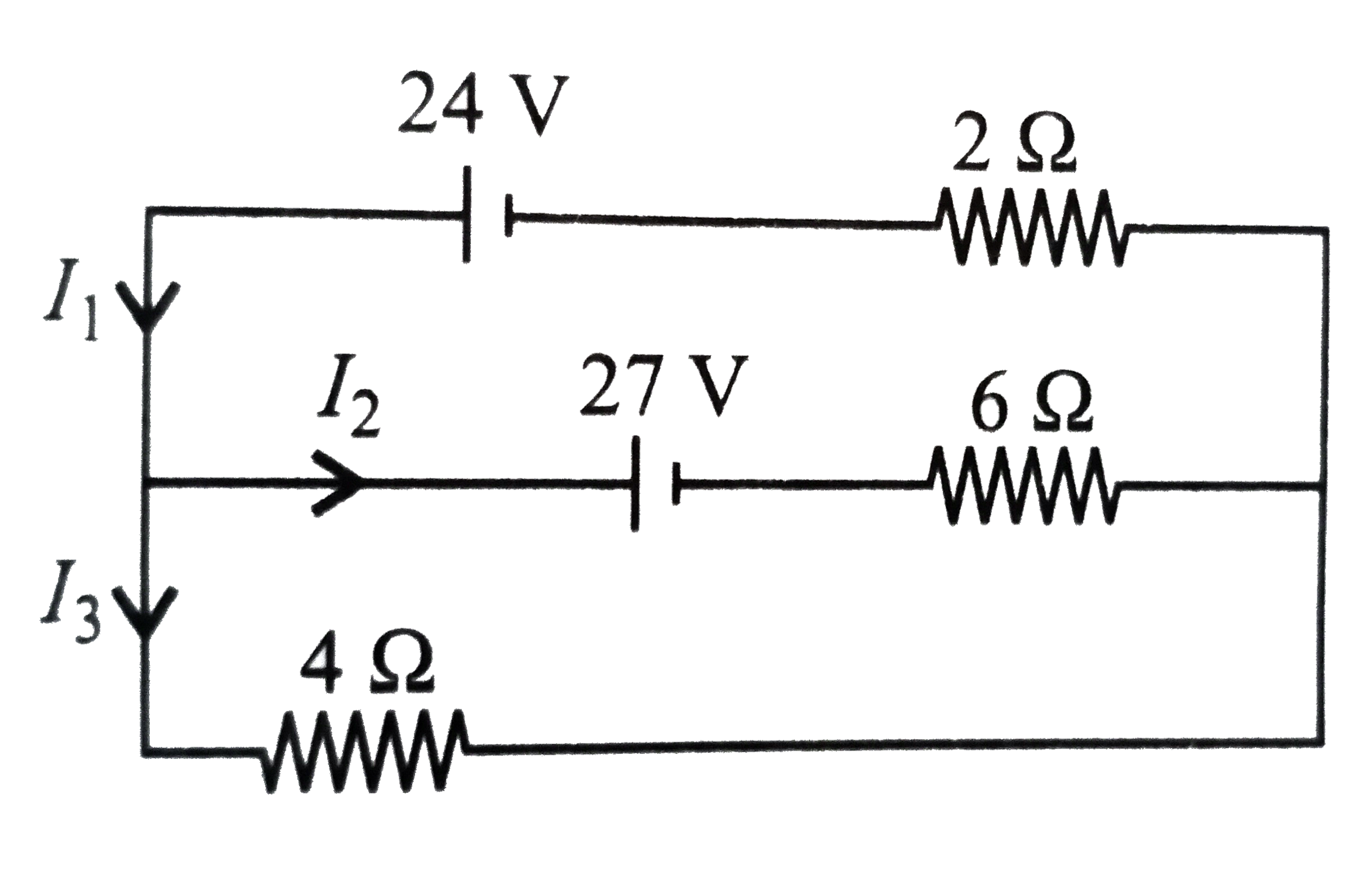 A3A,−3A2A,92AB92A,−32AC5A,4A,−3AD7A,54A,92A
A3A,−3A2A,92AB92A,−32AC5A,4A,−3AD7A,54A,92A
The value of (1+i)(1+i2)(1+i3)(1+i4) is a. 2 b. 0 c. 1 d. i
View SolutionThe value of (1+i)(1−i2)(1+i4)(1−i5) is
View SolutionThe value of (1+i)4+(1−i)4 is
View SolutionThe value of ∣∣∣12+i−12−i∣∣∣ is
View SolutionThe value of (1−i)31−i3 is equal to
View SolutionIf (1+i)(1+2i)(1+3i)...(1+ni)=a+ib, then the value of; 2.5.10.17...(1+n2 ) will be (a). a−ib (b). a2−b2 (c). a2+b2 (d). none of these
View SolutionIf Σ2ni=1sin−1xi=nπ , then find the value of Σ2ni=1xi.
View Solution