Let s be the standard deviation of n observations. Each of the n observations is multiplied by a constant c. Then the standard deviation of the resulting number is
s
cs
s√c
None of these
The correct Answer is:B
To solve the problem, we need to determine the standard deviation of a set of observations after each observation has been multiplied by a constant c. Let's go through the solution step by step.
1. Understanding Standard Deviation:
The standard deviation S of a set of n observations a1,a2,…,an is given by the formula:
S=
⎷1nn∑i=1(ai−¯x)2
where ¯x is the mean of the observations, calculated as:
¯x=a1+a2+…+ann
2. New Observations:
If each observation ai is multiplied by a constant c, the new observations become ca1,ca2,…,can.
3. Calculating the New Mean:
The mean of the new observations ¯x′ is:
¯x′=ca1+ca2+…+cann=c⋅a1+a2+…+ann=c⋅¯x
4. Calculating the New Standard Deviation:
The standard deviation of the new observations S′ is given by:
S′=
⎷1nn∑i=1(cai−¯x′)2
Substituting ¯x′=c¯x:
S′=
⎷1nn∑i=1(cai−c¯x)2
5. Factoring out the Constant:
We can factor out c from the expression:
S′=
⎷1nn∑i=1c2(ai−¯x)2
This simplifies to:
S′=
⎷c2⋅1nn∑i=1(ai−¯x)2=c⋅
⎷1nn∑i=1(ai−¯x)2
6. Final Result:
Since
⎷1nn∑i=1(ai−¯x)2 is the original standard deviation S, we have:
S′=c⋅S
Conclusion:
Thus, the standard deviation of the resulting observations after multiplying each observation by a constant c is:
S′=cS
The standard deviation S of a set of n observations a1,a2,…,an is given by the formula:
S=
⎷1nn∑i=1(ai−¯x)2
where ¯x is the mean of the observations, calculated as:
¯x=a1+a2+…+ann
If each observation ai is multiplied by a constant c, the new observations become ca1,ca2,…,can.
The mean of the new observations ¯x′ is:
¯x′=ca1+ca2+…+cann=c⋅a1+a2+…+ann=c⋅¯x
The standard deviation of the new observations S′ is given by:
S′=
⎷1nn∑i=1(cai−¯x′)2
Substituting ¯x′=c¯x:
S′=
⎷1nn∑i=1(cai−c¯x)2
We can factor out c from the expression:
S′=
⎷1nn∑i=1c2(ai−¯x)2
This simplifies to:
S′=
⎷c2⋅1nn∑i=1(ai−¯x)2=c⋅
⎷1nn∑i=1(ai−¯x)2
Since
⎷1nn∑i=1(ai−¯x)2 is the original standard deviation S, we have:
S′=c⋅S
Thus, the standard deviation of the resulting observations after multiplying each observation by a constant c is:
S′=cS
Similar Questions
Find the standard deviation of first n natural numbers.

View SolutionThe standard deviation for first 10 natural number is
View SolutionThe standard deviation of a distribution is 30. If each observation is increased by 5, then the new standard deviation will be
View SolutionThe mean and standard deviation of six observations are 8 and 4, respectively. If each observation is multiplied by 3, find the new mean and new standard deviation of the resulting observations.
View SolutionStandard deviation of first 'n' natural numbers is
View SolutionThe standard deviation of 25 numbers is 40. If each of the numbers in increased by 5, then the new standard deviation will be -
View SolutionCalculate the standard deviation of the following data:

View SolutionCalculate the standard deviation of the following data:

View SolutionFind the standard deviation of the following distribution :
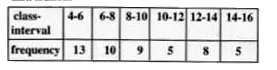
View SolutionFind the standard deviation for the following data

View Solution
