Read the following paragraph and answer the questions given below,
for a general reaction, , equilibrium constant is given by However, when all reactants and products are gases the equilibrium constant is generally expressed in terms of partial pressure.
For a reversible reaction , if concentration of the reactants are doubled, the equilibrium constant will be
times
times
2 times
remain same
The correct Answer is:D
To solve the question regarding the effect of doubling the concentration of reactants on the equilibrium constant Kc, we can follow these steps:
Step 1: Understand the Definition of Equilibrium Constant
The equilibrium constant Kc for a general reaction aA+bB⇌cC+dD is defined as:
Kc=(C)c(D)d(A)a(B)b
This equation shows the ratio of the concentrations of the products to the reactants at equilibrium.
Step 2: Write the Expression for Kc
For simplicity, consider a reaction where A converts to B:
A⇌B
The equilibrium constant Kc can be expressed as:
Kc=(B)(A)
Step 3: Analyze the Effect of Doubling Reactant Concentration
If we double the concentration of the reactant A, the new concentration of A becomes 2(A). The equilibrium expression now becomes:
Kc1=(B)(2A)=(B)2(A)
Step 4: Relate the New Equilibrium Constant to the Original
We can relate Kc1 to the original Kc:
Kc1=(B)2(A)=12⋅(B)(A)=Kc2
Step 5: Conclusion
From the above analysis, we see that when the concentration of the reactants is doubled, the new equilibrium constant Kc1 becomes half of the original equilibrium constant Kc. Therefore, the equilibrium constant remains unchanged in terms of its value; it is simply expressed in a different way due to the change in concentration.
Thus, the answer is that the equilibrium constant will be:
remains the same
The equilibrium constant Kc for a general reaction aA+bB⇌cC+dD is defined as:
Kc=(C)c(D)d(A)a(B)b
This equation shows the ratio of the concentrations of the products to the reactants at equilibrium.
For simplicity, consider a reaction where A converts to B:
A⇌B
The equilibrium constant Kc can be expressed as:
Kc=(B)(A)
If we double the concentration of the reactant A, the new concentration of A becomes 2(A). The equilibrium expression now becomes:
Kc1=(B)(2A)=(B)2(A)
We can relate Kc1 to the original Kc:
Kc1=(B)2(A)=12⋅(B)(A)=Kc2
From the above analysis, we see that when the concentration of the reactants is doubled, the new equilibrium constant Kc1 becomes half of the original equilibrium constant Kc. Therefore, the equilibrium constant remains unchanged in terms of its value; it is simply expressed in a different way due to the change in concentration.
remains the same
Similar Questions
For a general reaction, aA+bB⇔cC+dD,
equilibrium constant Kc is given by Kc=[C]c[D]d[A]a[B]b.
However, when all reactants and products are gases the equilibrium constant is generally expressed in terms of partial pressure.
Kp=PcC×PdDPaA×PbB
In which of the following equilibrium will shift forward on addition of inert gas at constant pressure ?
View SolutionFor the reaction, A+2B⇔C, the expession for equilibrium constant is
View Solution
Knowledge Check
Which of the following relations between the reactions and equilibrium constant for a general reaction aA+bB⇔cC+dD is not correct ?
A(1) aA+bB⇔cC+dD:KcB(2) cC+dD⇔aA+bB:K′c=1KcC(3) naA+nbB⇔ncC+ndD:K''c=KncD(4) aA+bB⇔cC+dD:Kc=Kp
For a gaseous reaction 2B→A, the equilibrium constant Kp is ……… to/than Kc.
View SolutionFor reaction 2A+B⇔2C,K=x
Equilibrium constant for C⇔A+1/2B will be
View SolutionFor a given reversible reaction at a fixed temperature, equilibrium constants Kp and Kc are related by ………
View SolutionIn the reversible reaction A + B ⇔ C + D, the concentration of each C and D at equilobrium was 0.8 mole/litre, then the equilibrium constant Kc will be
View SolutionThe unit of equilibrium constant Kc for the reaction A+B⇔C would be
View SolutionThe equilibrium constant for a reaction
A+2B⇔2C is 40. The equilibrium constant for reaction C⇔B+1/2A is
View SolutionConsider the reaction, A+B→C+D.
The initial rate for different initial concentrations of the reactants are given below :
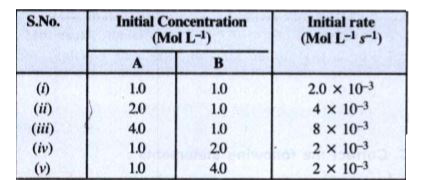
Calculate the rate constant.
View Solution
