A tube of uniform cross sectional area 1cm−2 is closed at one end with semi permeable mebrane. A solution having 5 gm glucose per glucose per 100 ml is placed inside the tube and dipped in pure water at 27∘C. When the equilibrium is established. what will be the osmotic pressure height developed in vertical column. Also caiculate molality and molarity of the solution Density of glucose is 1gm/ml.
The correct Answer is:0.29
To solve the given problem, we need to calculate the osmotic pressure, height of the liquid column, molarity, and molality of the glucose solution. Let's break this down step by step.
Step 1: Calculate Molarity of the Solution
Given:
- Mass of glucose (W) = 5 g
- Volume of solution (V) = 100 ml = 0.1 L
- Molar mass of glucose (C6H12O6) = 180 g/mol
Formula for Molarity (M):
M=WB×1000MB×V
Calculation:
M=5g×1000180g/mol×100ml=500018000≈0.2778mol/L≈0.28mol/L
Step 2: Calculate Molality of the Solution
Given:
- Weight of the solvent (water) = 100 ml of water = 100 g (assuming density of water is 1 g/ml)
- Weight of glucose (W_B) = 5 g
- Weight of solution (W_A) = 100 g (water) + 5 g (glucose) = 105 g
Formula for Molality (m):
m=WB×1000MB×WA
Calculation:
m=5g×1000180g/mol×95g=500017100≈0.2924mol/kg≈0.29mol/kg
Step 3: Calculate Osmotic Pressure
Formula for Osmotic Pressure (π):
π=nRTV
Where:
- n = number of moles of solute
- R = ideal gas constant = 0.0821 L·atm/(K·mol)
- T = temperature in Kelvin = 27°C + 273 = 300 K
Calculate number of moles (n):
n=WBMB=5g180g/mol≈0.02778mol
Volume (V) in liters:
V=0.1L
Calculation of Osmotic Pressure:
π=0.02778mol×0.0821L⋅atm/(K⋅mol)×300K0.1L≈6.841atm
Step 4: Calculate Height of the Liquid Column
Using the formula:
π=h⋅ρ⋅g
Where:
- h = height of the liquid column (in meters)
- ρ = density of the liquid (water) = 1000 kg/m³
- g = acceleration due to gravity = 9.81 m/s²
Rearranging the formula to find height (h):
h=πρ⋅g
Calculation:
h=6.841atm×101325Pa/atm1000kg/m3×9.81m/s2≈7070.85cm≈70.71m
Final Results:
- Molarity (M) ≈ 0.28 mol/L
- Molality (m) ≈ 0.29 mol/kg
- Height of the liquid column (h) ≈ 70.71 m
---
- Mass of glucose (W) = 5 g
- Volume of solution (V) = 100 ml = 0.1 L
- Molar mass of glucose (C6H12O6) = 180 g/mol
M=WB×1000MB×V
M=5g×1000180g/mol×100ml=500018000≈0.2778mol/L≈0.28mol/L
- Weight of the solvent (water) = 100 ml of water = 100 g (assuming density of water is 1 g/ml)
- Weight of glucose (W_B) = 5 g
- Weight of solution (W_A) = 100 g (water) + 5 g (glucose) = 105 g
m=WB×1000MB×WA
m=5g×1000180g/mol×95g=500017100≈0.2924mol/kg≈0.29mol/kg
π=nRTV
- n = number of moles of solute
- R = ideal gas constant = 0.0821 L·atm/(K·mol)
- T = temperature in Kelvin = 27°C + 273 = 300 K
n=WBMB=5g180g/mol≈0.02778mol
V=0.1L
π=0.02778mol×0.0821L⋅atm/(K⋅mol)×300K0.1L≈6.841atm
π=h⋅ρ⋅g
- h = height of the liquid column (in meters)
- ρ = density of the liquid (water) = 1000 kg/m³
- g = acceleration due to gravity = 9.81 m/s²
h=πρ⋅g
h=6.841atm×101325Pa/atm1000kg/m3×9.81m/s2≈7070.85cm≈70.71m
- Molarity (M) ≈ 0.28 mol/L
- Molality (m) ≈ 0.29 mol/kg
- Height of the liquid column (h) ≈ 70.71 m
Similar Questions
A tube of uniform cross-sectional area 1cm2 is closed at one end with semi-permeable membrane. A solution of 5g glucose per 100mL is placed inside the tube and is dipped in pure water at 27∘C. When equilibrium is established, calculate:
a. The osmotic pressure of solution.
b.The height developed in vertical column.
Assume the density of final glucose solution 1gmL−1
View SolutionA solution of glucose (molar mass=180gmol−1) in water is labelled as 10% (by mass). What would be the molarity and molality of the solution? Given that the density of the solution is 1.2gmL−1.
View SolutionA solution contain 8 g of a carbohydrate in 100 g of water has a density 1.025 g/mL and an osmotic pressure of 5 atm at 27∘C. What is the molar mass of the carbohydrate?
View SolutionTorricelli was the first do devise an experiment for measuring atmospheric pressure . He took calibrated hard glass tube , 1 m in lengt and of uniform cross section , closed at one end . He filled the whole tube with dry mercury taking care than no air or water droplets remain inside the tube , closed the opposite end of the tube tightly with thumb and inverted it . He put this inverted mercury tube into a mercury through , taking care that the end of the tube remains inside the mercury through , An interesting thing was noticed . Mercury in the tube fell down at first and then stopped at a particular position . The height was 76 cm above the free surface of mercury in the through . When the given tube was inclined or lowered in the mercury trough , the vertical haight of mercury level in the tube was always found constant .
Torricelli explained this by saying that the free surface of mercury in the trough . Hence , the hydrostatic pressure exerted by the trough measures the atmospheric pressure .
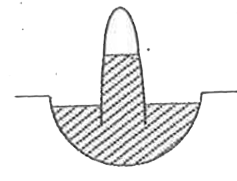
If this expriment uses water instead of mercury , then
A. length of water will be equal to 76 cm
B. length of water will be less than 76 cm
C. length of water will be greater than 76 cm
D. none of the above
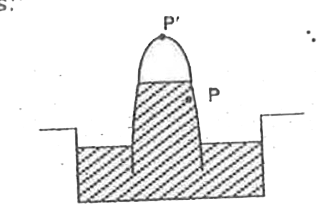
View SolutionTorricelli was the first do devise an experiment for measuring atmospheric pressure . He took calibrated hard glass tube , 1 m in lengt and of uniform cross section , closed at one end . He filled the whole tube with dry mercury taking care than no air or water droplets remain inside the tube , closed the opposite end of the tube tightly with thumb and inverted it . He put this inverted mercury tube into a mercury through , taking care that the end of the tube remains inside the mercury through , An interesting thing was noticed . Mercury in the tube fell down at first and then stopped at a particular position . The height was 76 cm above the free surface of mercury in the through . When the given tube was inclined or lowered in the mercury trough , the vertical haight of mercury level in the tube was always found constant .
Torricelli explained this by saying that the free surface of mercury in the trough . Hence , the hydrostatic pressure exerted by the trough measures the atmospheric pressure .
If an additional hole is also made at P ' at the top point of the tube , then

A. mercury will not come out of the tube
B. mercury may come out of the tube after some time .
C. mercury will come out of the tube instantly
D. none of these
View SolutionTorricelli was the first do devise an experiment for measuring atmospheric pressure . He took calibrated hard glass tube , 1 m in lengt and of uniform cross section , closed at one end . He filled the whole tube with dry mercury taking care than no air or water droplets remain inside the tube , closed the opposite end of the tube tightly with thumb and inverted it . He put this inverted mercury tube into a mercury through , taking care that the end of the tube remains inside the mercury through , An interesting thing was noticed . Mercury in the tube fell down at first and then stopped at a particular position . The height was 76 cm above the free surface of mercury in the through . When the given tube was inclined or lowered in the mercury trough , the vertical haight of mercury level in the tube was always found constant .
Torricelli explained this by saying that the free surface of mrcury in the trough . Hence , the hydrostatic pressure exerted by the trough measures the atmospheric pressure .

If a small hole is made at point P in the barometer tube , then
View SolutionThe cylinderical tube of a spray pump has a cross-section of 8.0cm2 one end of which has 40 fine holes each of diameter 1.0mm. If the liquid flow inside the tube is 1.5 m per minute, what is the speed of ejection of the liquid through the holes?
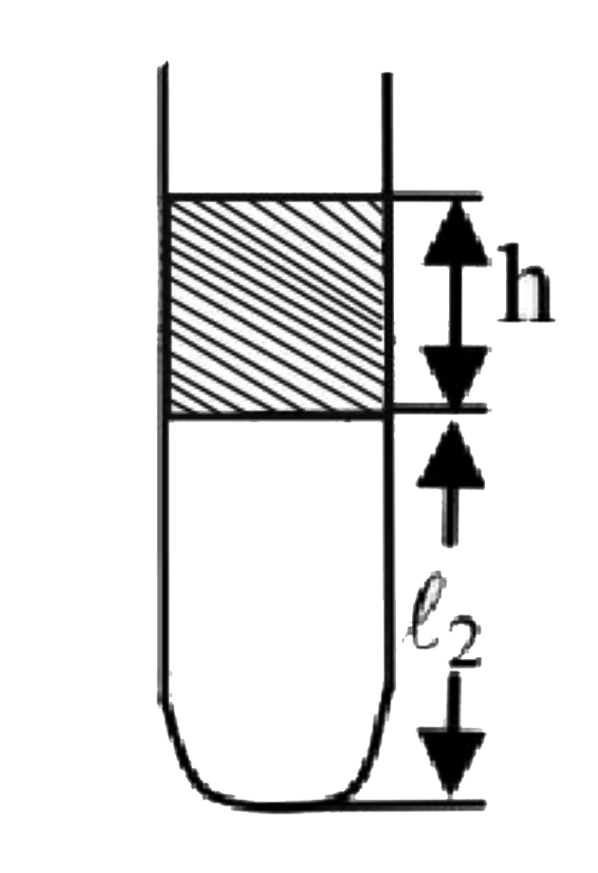
View SolutionAn air column closed in a tube sealed at one end by a Hg column having height h. When the tube is placed with open end down, the height of the air column Iis l1. If the tube is turned so that its open end is at the top, the height of the air column is l2. What is the atmospheric pressure (P0).
View SolutionA U-tube having horizontal arm of length 20 cm, has uniform cross-sectional area=1cm2, It is filled with water of volume 60 cc. What volume of a liquid of density 4g/ should be poured from one side into the U-tube so that no water is left in the horizontal arm of the tube? a) 60 cc b) 45 cc c) 50 cc d) 35 cc
View SolutionThe vapour pressure of a solvent in a solution is lower than that of pure solvent, at the same temperature. A higher temperature is needed to raise the vapour pressure up to the atmospheric pressure, when boiling begins. However, increase is small, like 0.1molkg−1 aqueous sucrose solution boils at 100.05∘C.
Sea water, an aqueous solution, which is rich in Na+ and Cl− ions, freezes about 1∘C lower than frozen water. At the freezing point of a pure solvent, the rates at which two molecules stick together to form the solid and leave it to return to liquid state are equal when solute is present. Fewer solvent molecules are in contact with surface of solid. However, the rate at which the solvent molecules leave the surface of solid remains unchanged. That is why temperature is lowered to restore the equilibrium. The freezing point depression in an ideal solution is proportional to molality of the solute.
Whene 250 m,g of eugenol is added to 100 gm of camphor (Kf=37.9), it lowered the freezing point by 0.62∘C, the molar mass of eugenol is
View Solution
