In one dimensional motin, a 1 kg body experiences a force, which is linear function of time t viz. F=2t acting in the direction of motion. What is the work done by the force in the first 4 second?
16J
32J
64J
128J
The correct Answer is:D
To solve the problem of calculating the work done by a force that is a linear function of time, we can follow these steps:
Step 1: Understand the Force Function
The force acting on the body is given by the equation:
F(t)=2t
This means that the force changes linearly with time.
Step 2: Relate Force to Acceleration
Using Newton's second law, we know that:
F=ma
where m is the mass of the body (1 kg) and a is the acceleration. Therefore, we can express acceleration as:
a=Fm=2t1=2t
Step 3: Relate Acceleration to Velocity
Acceleration is the derivative of velocity with respect to time:
a=dvdt
Thus, we can write:
dvdt=2t
Step 4: Integrate to Find Velocity
To find the velocity as a function of time, we integrate the acceleration:
dv=2tdt
Integrating both sides from t=0 to t=t:
∫dv=∫2tdt
This gives:
v(t)=t2+C
Since the initial velocity v(0)=0, we have C=0. Therefore:
v(t)=t2
Step 5: Calculate Work Done
The work done by the force over a time interval can be calculated using the integral:
W=∫F⋅ds
Since ds=vdt, we can rewrite this as:
W=∫F(t)v(t)dt
Substituting the expressions for F(t) and v(t):
W=∫40(2t)(t2)dt
This simplifies to:
W=∫402t3dt
Step 6: Evaluate the Integral
Now we evaluate the integral:
W=2∫40t3dt
Calculating the integral:
∫t3dt=t44
Thus:
W=2(t44)40=2(444−044)
Calculating 44=256:
W=2(2564)=2×64=128Joules
Final Answer
The work done by the force in the first 4 seconds is:
128Joules
The force acting on the body is given by the equation:
F(t)=2t
This means that the force changes linearly with time.
Using Newton's second law, we know that:
F=ma
where m is the mass of the body (1 kg) and a is the acceleration. Therefore, we can express acceleration as:
a=Fm=2t1=2t
Acceleration is the derivative of velocity with respect to time:
a=dvdt
Thus, we can write:
dvdt=2t
To find the velocity as a function of time, we integrate the acceleration:
dv=2tdt
Integrating both sides from t=0 to t=t:
∫dv=∫2tdt
This gives:
v(t)=t2+C
Since the initial velocity v(0)=0, we have C=0. Therefore:
v(t)=t2
The work done by the force over a time interval can be calculated using the integral:
W=∫F⋅ds
Since ds=vdt, we can rewrite this as:
W=∫F(t)v(t)dt
Substituting the expressions for F(t) and v(t):
W=∫40(2t)(t2)dt
This simplifies to:
W=∫402t3dt
Now we evaluate the integral:
W=2∫40t3dt
Calculating the integral:
∫t3dt=t44
Thus:
W=2(t44)40=2(444−044)
Calculating 44=256:
W=2(2564)=2×64=128Joules
The work done by the force in the first 4 seconds is:
128Joules
Similar Questions
A force acts on a 2 kg object so that its position is given as a function of time as x=3t2+5. What is the work done by this force in first 5 seconds ?
View SolutionUnder the action of a force, a 2kg body moves such that its position x as a function of time is given by x=t33 where x is in meter and t in second. The work done by the force in the first two seconds is .
View Solution
Knowledge Check
- Question 1 - Select One
A body of mass 3kg is under a force , which causes a displacement in it is given by S=t33 (in metres). Find the work done by the force in first 2 seconds.
A2JB3.8 JC5.2 JD2.6 J
Under the action of a force, a 2kg body moves such that its position x as a function of time is given by x=t33 where x is in metre and t in second. The work done by the force in the first two seconds is .
View SolutionUnder the action of a force, a 1 kg body moves, such that its position x as function of time t is given by x=t32. where x is in meter and t is in second. The work done by the force in fiest 3 second is
View SolutionThe distance x moved by a body of mass 0.5 kg under the action of a force varies with time t as
x(m)=3t2+4t+5
Here, t is expressed in second. What is the work done by the force in first 2 seconds?View SolutionThe force F acting on a particle is moving in a straight line as shown in figure. What is the work done by the force on the particle in the 4 m of the trajectory?
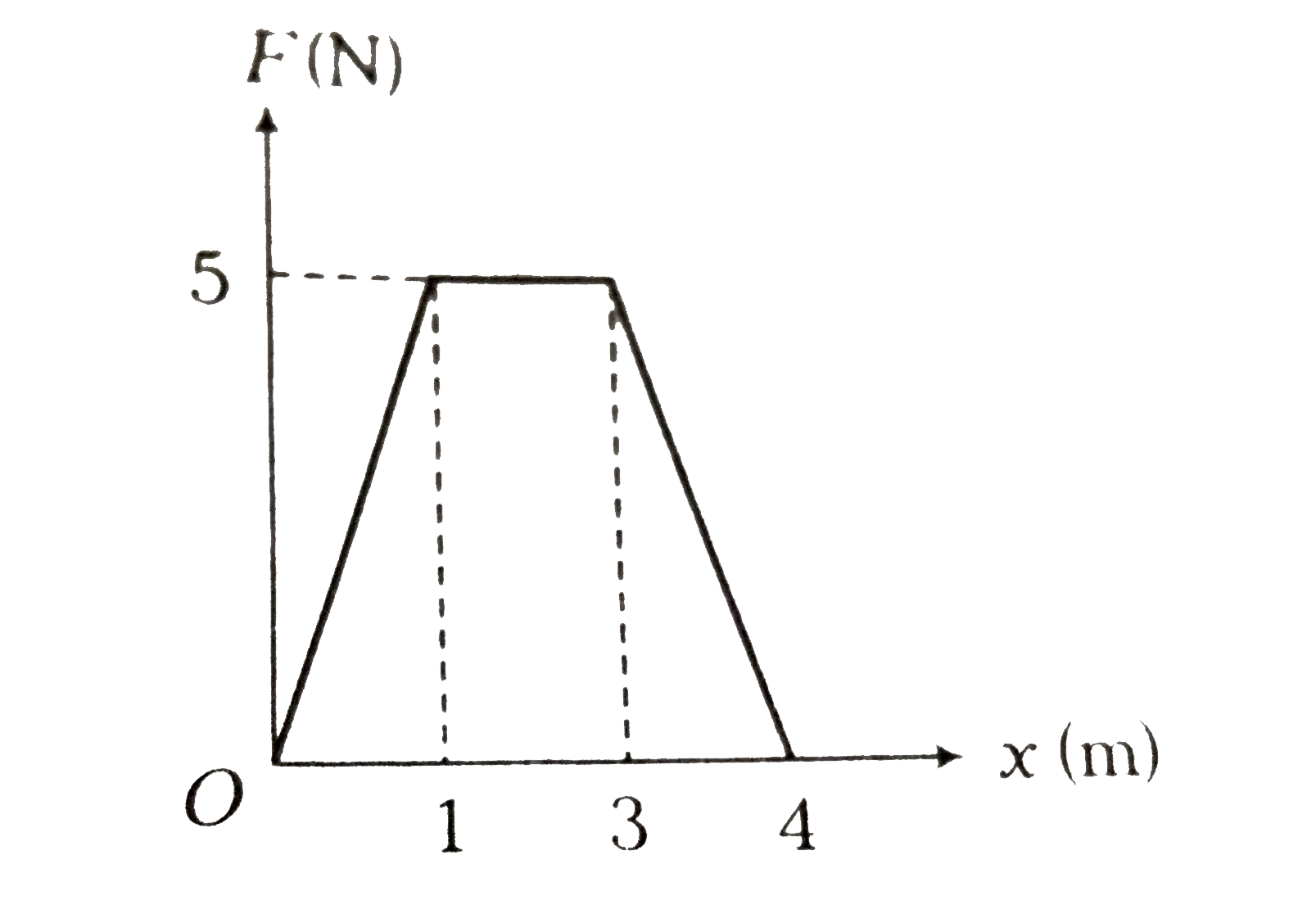 View Solution
View SolutionUnder the action of foece, 1 kg body moves such that its position x as a function of time t is given by x=t33, x is meter. Calculate the work done (in joules) by the force in first 2 seconds.
View SolutionA time dependent force F=6t acts on a particle of mass 1kg. If the particle starts from rest, the work done by the force during the first 1sec. will be
View SolutionA body of mass 6kg is under a force which causes displacement in it given by S=t24 maters where t is time . The work done by the force in 2 sec is
View Solution

