Two small blcok m=2kg each kept on wedge of mass 12kg. There is no friction between blocks and wedge coefficient of friction between wedge and ground in μ=0.3. Calculate frictional force by ground on wedge.
The correct Answer is:(a) x=0, (b) √32gR
To solve the problem, we need to analyze the forces acting on the wedge and the blocks placed on it. Here's a step-by-step solution:
Step 1: Identify the masses and angles
- Mass of each block, m=2kg
- Mass of the wedge, M=12kg
- Coefficient of friction between the wedge and the ground, μ=0.3
- The angle of the wedge is θ=30∘ (since the blocks are resting on the wedge which is inclined).
Step 2: Calculate the gravitational force acting on the blocks
The gravitational force acting on each block is given by:
Fg=m⋅g
where g≈9.81m/s2.
For each block:
FgA=2kg⋅9.81m/s2=19.62N
FgB=2kg⋅9.81m/s2=19.62N
Step 3: Determine the normal forces acting on the blocks
The normal force N acting on each block can be calculated using the angle of the wedge. The normal force for each block is given by:
NA=m⋅g⋅cos(30∘)
NB=m⋅g⋅cos(30∘)
Calculating NA and NB:
NA=2⋅9.81⋅cos(30∘)≈2⋅9.81⋅0.866≈17.02N
NB=2⋅9.81⋅cos(30∘)≈17.02N
Step 4: Calculate the horizontal components of the normal forces
The horizontal components of the normal forces acting on the wedge due to the blocks are:
FhorizontalA=NA⋅sin(30∘)=17.02⋅0.5=8.51N
FhorizontalB=NB⋅sin(30∘)=17.02⋅0.5=8.51N
Step 5: Determine the net horizontal force on the wedge
Since both horizontal components act in opposite directions, they cancel each other out:
Fnet=FhorizontalA−FhorizontalB=8.51−8.51=0N
Step 6: Calculate the maximum static friction force between the wedge and the ground
The maximum static friction force Ffriction that can act on the wedge is given by:
Ffriction=μ⋅Nwedge
where Nwedge is the normal force acting on the wedge due to its weight:
Nwedge=M⋅g=12⋅9.81≈117.72N
Thus,
Ffriction=0.3⋅117.72≈35.32N
Step 7: Conclusion
Since the net horizontal force on the wedge is zero, the frictional force exerted by the ground on the wedge will also be zero because there is no net force trying to move the wedge.
Final Answer
The frictional force by the ground on the wedge is:
Frictional Force=0N
- Mass of each block, m=2kg
- Mass of the wedge, M=12kg
- Coefficient of friction between the wedge and the ground, μ=0.3
- The angle of the wedge is θ=30∘ (since the blocks are resting on the wedge which is inclined).
The gravitational force acting on each block is given by:
Fg=m⋅g
where g≈9.81m/s2.
FgA=2kg⋅9.81m/s2=19.62N
FgB=2kg⋅9.81m/s2=19.62N
The normal force N acting on each block can be calculated using the angle of the wedge. The normal force for each block is given by:
NA=m⋅g⋅cos(30∘)
NB=m⋅g⋅cos(30∘)
NA=2⋅9.81⋅cos(30∘)≈2⋅9.81⋅0.866≈17.02N
NB=2⋅9.81⋅cos(30∘)≈17.02N
The horizontal components of the normal forces acting on the wedge due to the blocks are:
FhorizontalA=NA⋅sin(30∘)=17.02⋅0.5=8.51N
FhorizontalB=NB⋅sin(30∘)=17.02⋅0.5=8.51N
Since both horizontal components act in opposite directions, they cancel each other out:
Fnet=FhorizontalA−FhorizontalB=8.51−8.51=0N
The maximum static friction force Ffriction that can act on the wedge is given by:
Ffriction=μ⋅Nwedge
where Nwedge is the normal force acting on the wedge due to its weight:
Nwedge=M⋅g=12⋅9.81≈117.72N
Thus,
Ffriction=0.3⋅117.72≈35.32N
Since the net horizontal force on the wedge is zero, the frictional force exerted by the ground on the wedge will also be zero because there is no net force trying to move the wedge.
The frictional force by the ground on the wedge is:
Frictional Force=0N
Similar Questions
Calculate angle of friction between wedge and block system is at rest M coefficient of friction between wedge and block.
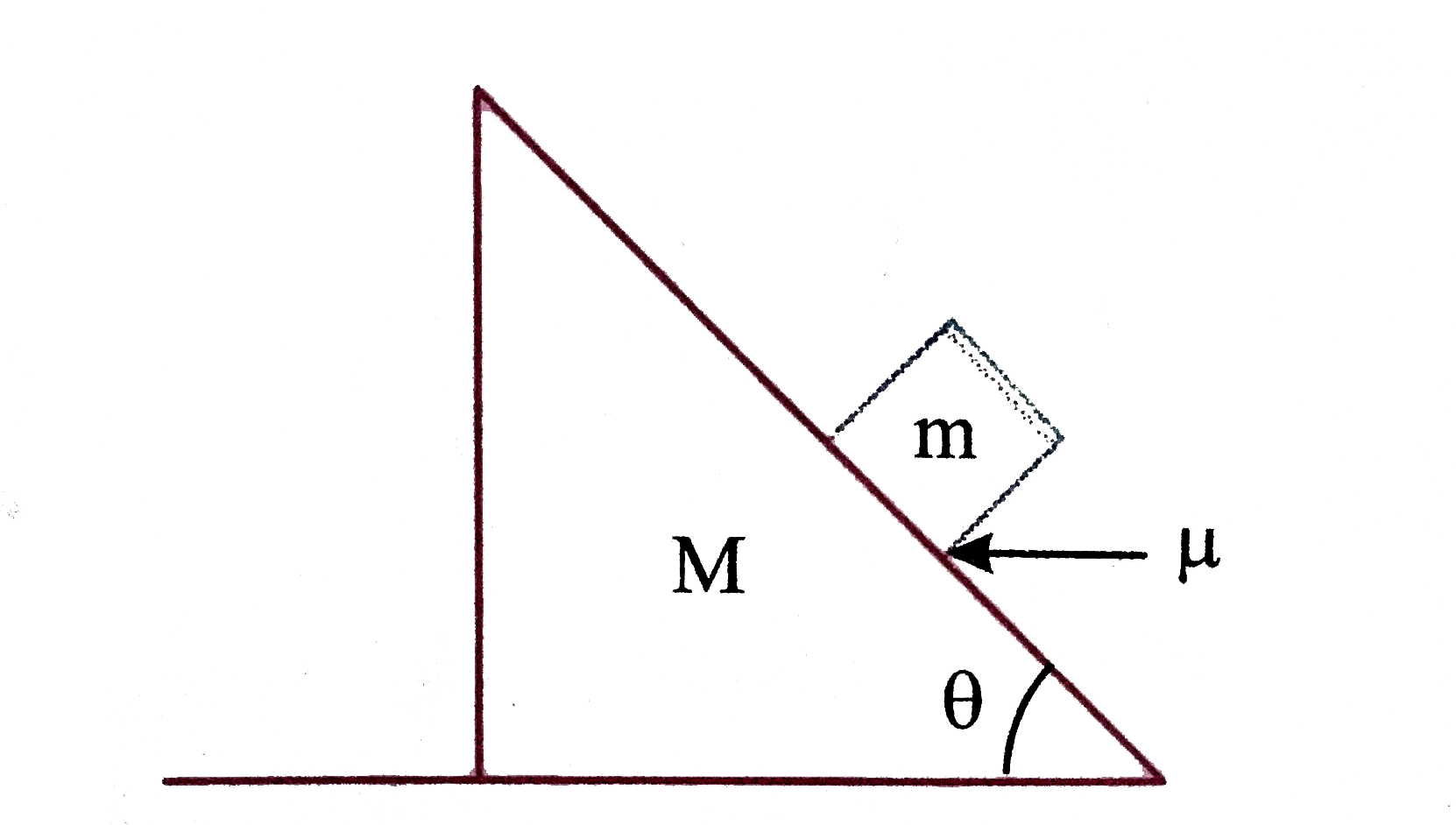
View Solutiona Block of mass m is placed on a wedge of mass M there is no friction between the block and the wedge .The minmum coefficient of friction between the wedge and the gound so that wedge does not move is,
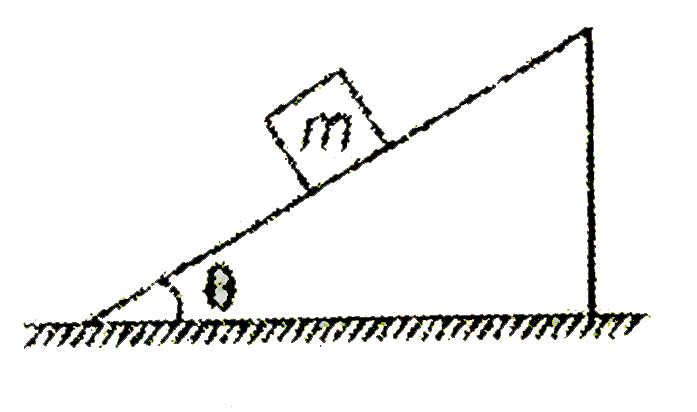
View SolutionA cube of mass m is placed on top of a wedge of mass 2m, as shown in figure. There is no friction between the cube and the wedge. The minimum co - efficient of friction between the wedge and the horizontal surface, so that the wedge does not move is
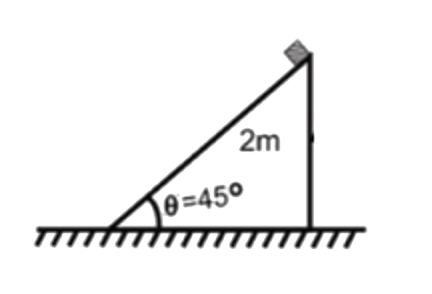
View SolutionIn the show arrangement mass of A=1 kg, mass of B= 2kg. Coefficient of friction between A and B =0.2

There is no friction between B and ground. The frictional force exerted by A on B equals.
View SolutionA block A with mass 100kg is resting on another block B of mass 200kg. As shown in figure a horizontal rope tied to a wall hold it. The coefficient of friction between A and B is 0.2 while coefficient of friction between B and the ground is 0.3 . the minimum required force F to start moving B will be.

View SolutionA block A with mass 100kg is resting on another block B of mass 200kg. As shown in figure a horizontal rope tied to a wall hold it. The coefficient of friction between A and B is 0.2 while coefficient of friction between B and the ground is 0.3 . the minimum required force F to start moving B will be.

View SolutionA block A with mass 100kg is resting on another block B of mass 200kg. As shown in figure a horizontal rope tied to a wall hold it. The coefficient of friction between A and B is 0.2 while coefficient of friction between B and the ground is 0.3 . the minimum required force F to start moving B will be.

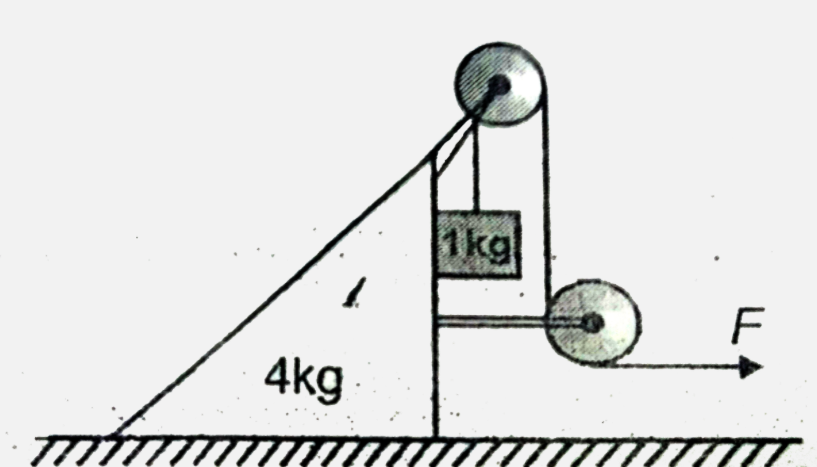
View SolutionAn arrangement is shown in the figure . The mass of the wedge is 4 kg and that of the block is 1 kg . There is no friction between wedge and ground , but coefficient of friction between vertical surface of the wedge and to the block is mu= 0.1. . (Assume ideal pulley and string) (g = 10m/s2) and assuming the pulley to be massless and friction. calucalate the maximum possible values of force upto while bock remain stationary relative to wedge.
View SolutionA block of mass m is at rest on wedge as shown in figure. Let N be the normal reaction between two and f the force of friction, then choose the wrong option.
View SolutionA block on table shown in figure is just on the wedge of slipping. Find the coefficient of static friction between the block and table top.

View Solution
