Question

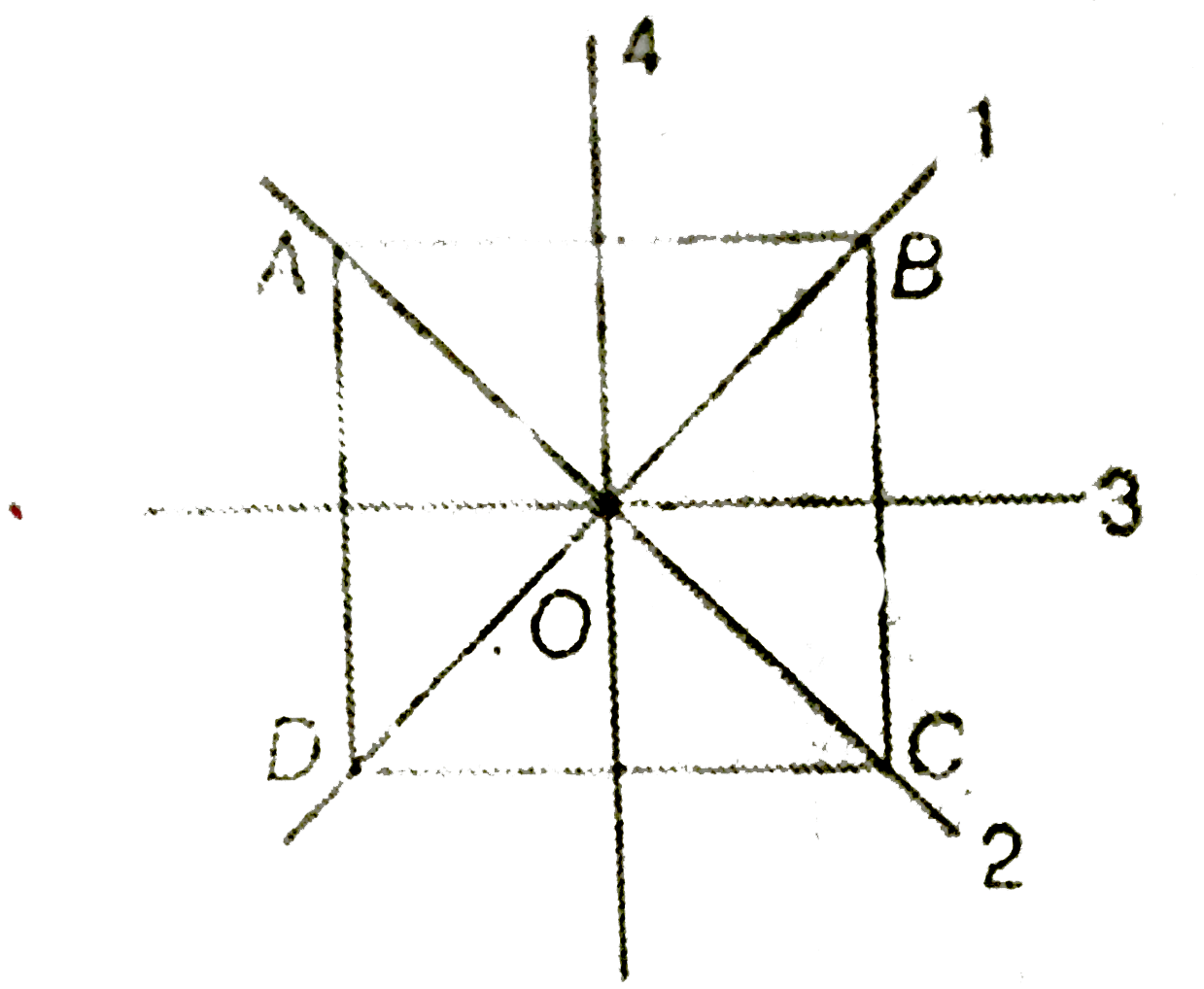
Consider a uniform square plate shown in the figure. $I_1$,$I_2$, $I_3$ and $I_4$ are moment of inertia of the plate about the axes 1, 2, 3 and 4 respectively. Axes 1 and 2 are diagonals and 3 and 4 are lines passing through centre parallel to sides of the square. The moment of inertia of the plate about an axis passing through centre and perpendicular to the plane of the figure is equal to which of the followings.

A. $I_3$ + $I_4$
B. $I_1$ + $I_3$
C. $I_2$ + $I_3$
D. $\frac{1}{2}$ $(I_1+I_2+I_3+I_4)$

Options

A. `I_3` + `I_4`
B. `I_1` + `I_3`
C. `I_2` + `I_3`
D. 1/2`(I_1+I_2+I_3+I_4)`

Answer

3

Explanation

To solve the problem, we need to find the moment of inertia of a uniform square plate about an axis passing through its center and perpendicular to its plane. We will use the perpendicular axis theorem, which states that for a flat plate lying in the XY plane, the moment of inertia about an axis perpendicular to the plane (Iz) is equal to the sum of the moments of inertia about two perpendicular axes lying in the plane (Ix and Iy).

1. Identify the Axes and Moments of Inertia:
- Let \( I_1 \) and \( I_2 \) be the moments of inertia about the diagonals of the square plate.
- Let \( I_3 \) and \( I_4 \) be the moments of inertia about the axes parallel to the sides of the square plate.

2. Apply the Perpendicular Axis Theorem:
According to the perpendicular axis theorem:
\( I_z = I_x + I_y \)
where \( I_z \) is the moment of inertia about the axis perpendicular to the plane, and \( I_x \) and \( I_y \) are the moments of inertia about two perpendicular axes in the plane.

3. Relate the Moments of Inertia:
Since the square plate is uniform, we have:
\( I_1 = I_2 = I_3 = I_4 \)
This means that all the moments of inertia about the axes are equal.

4. Combine the Moments of Inertia:
From the previous step, we can express \( I_z \) in terms of \( I_1 \) and \( I_3 \):
\( I_z = I_1 + I_2 = I_1 + I_1 = 2I_1 \)
Similarly, we can express it using \( I_3 \) and \( I_4 \):
\( I_z = I_3 + I_4 = I_3 + I_3 = 2I_3 \)

5. Calculate \( I_z \):
Now, if we add all four moments of inertia:
\( I_1 + I_2 + I_3 + I_4 = 4I_1 \)
Thus, we can relate \( I_z \) to the total moment of inertia:
\( I_z = \frac{1}{2}(I_1 + I_2 + I_3 + I_4) \)

6. Conclusion:
Therefore, the moment of inertia of the plate about an axis passing through the center and perpendicular to the plane is:
\( I_z = \frac{1}{2}(I_1 + I_2 + I_3 + I_4) \)
This corresponds to option D.

Final Answer:
The moment of inertia of the plate about an axis passing through the center and perpendicular to the plane of the figure is equal to:
D. \( \frac{1}{2}(I_1 + I_2 + I_3 + I_4) \)