Two cylinders A and B are at rest in a box as shown in the figure. Cylinder A has a diameter of 3d and mass 120 kg. Cylinder B has a diameter of 2d and mass 36 kg . The width of the box is 4.5d. If all the contact surfaces are assumed to be smooth, then find the normal force exerted by the left wall on the cylinder B.
1200N
1600N
2000 N
nothing can be said
The correct Answer is:B
To solve the problem of finding the normal force exerted by the left wall on cylinder B, we can follow these steps:
Step 1: Understand the Setup
We have two cylinders, A and B, resting in a box. Cylinder A has a diameter of 3d and a mass of 120 kg, while cylinder B has a diameter of 2d and a mass of 36 kg. The width of the box is 4.5d.
Step 2: Identify the Forces Acting on Cylinder B
Since the surfaces are smooth, the only forces acting on cylinder B are:
- The normal force exerted by the left wall on cylinder B (let's denote it as N1).
- The normal force exerted by cylinder A on cylinder B (let's denote it as N3).
- The weight of cylinder B acting downwards (W = m_B * g).
Step 3: Determine the Angles
To find the relationship between the forces, we need to find the angle θ formed by the line connecting the centers of the two cylinders and the vertical.
- The horizontal distance from the left wall to the center of cylinder B is d (half of its diameter).
- The vertical distance from the top of cylinder B to the center of cylinder A is 1.5d (half of cylinder A's diameter minus half of cylinder B's diameter).
Using the Pythagorean theorem:
- The hypotenuse (h) = √(d² + (1.5d)²) = √(d² + 2.25d²) = √(3.25d²) = √(13/4)d = (√13/2)d.
Step 4: Calculate Cosine and Sine of θ
Using the triangle formed:
- cos(θ) = adjacent/hypotenuse = d / ((√13/2)d) = 2/√13.
- sin(θ) = opposite/hypotenuse = 1.5d / ((√13/2)d) = 3/√13.
Step 5: Apply Equilibrium Conditions
Since the system is at rest, we can apply the equilibrium conditions:
1. In the vertical direction:
N3⋅sin(θ)=WB
where WB=mB⋅g=36⋅10=360N.
Substituting the values:
N3⋅3√13=360⟹N3=360⋅√133=120√13N.
2. In the horizontal direction:
N1=N3⋅cos(θ).
Substituting the values:
N1=120√13⋅2√13=240N.
Step 6: Conclusion
The normal force exerted by the left wall on cylinder B is N1=240N.
We have two cylinders, A and B, resting in a box. Cylinder A has a diameter of 3d and a mass of 120 kg, while cylinder B has a diameter of 2d and a mass of 36 kg. The width of the box is 4.5d.
Since the surfaces are smooth, the only forces acting on cylinder B are:
- The normal force exerted by the left wall on cylinder B (let's denote it as N1).
- The normal force exerted by cylinder A on cylinder B (let's denote it as N3).
- The weight of cylinder B acting downwards (W = m_B * g).
To find the relationship between the forces, we need to find the angle θ formed by the line connecting the centers of the two cylinders and the vertical.
- The horizontal distance from the left wall to the center of cylinder B is d (half of its diameter).
- The vertical distance from the top of cylinder B to the center of cylinder A is 1.5d (half of cylinder A's diameter minus half of cylinder B's diameter).
- The hypotenuse (h) = √(d² + (1.5d)²) = √(d² + 2.25d²) = √(3.25d²) = √(13/4)d = (√13/2)d.
Using the triangle formed:
- cos(θ) = adjacent/hypotenuse = d / ((√13/2)d) = 2/√13.
- sin(θ) = opposite/hypotenuse = 1.5d / ((√13/2)d) = 3/√13.
Since the system is at rest, we can apply the equilibrium conditions:
1. In the vertical direction:
N3⋅sin(θ)=WB
where WB=mB⋅g=36⋅10=360N.
N3⋅3√13=360⟹N3=360⋅√133=120√13N.
N1=N3⋅cos(θ).
Substituting the values:
N1=120√13⋅2√13=240N.
The normal force exerted by the left wall on cylinder B is N1=240N.
Similar Questions
_S01_081_Q01.png)
A cylinder fitted with piston as shown in figure. The cylinder is filled with water and is taken to a place where there is no gravity mass of the piscton is 50 kg. the system is accelerated with acceleration 0.5m/sec2 in positive x-direction find the force exerted by fluid on the surface AB of the cylinder in decanewton. Take area of cross-section of cylinder to be 0.01 m2 and neglect atmospheric pressure (1 deca newton=10N)View SolutionA man of mass 40 kg is at rest between the walls as shown in the figure. If between the man and the walls is 0.8, find the normal reaction exerted by the walls on the man. (g = 10ms−2)
 View Solution
View SolutionA cylinder of mass M and radius r is suspended at the corner of a room. Length of the thread is twice the radius of the cylinder. Find the tension in the thread and normal force applied by each wall on the cylinder assuming the walls to be smooth.
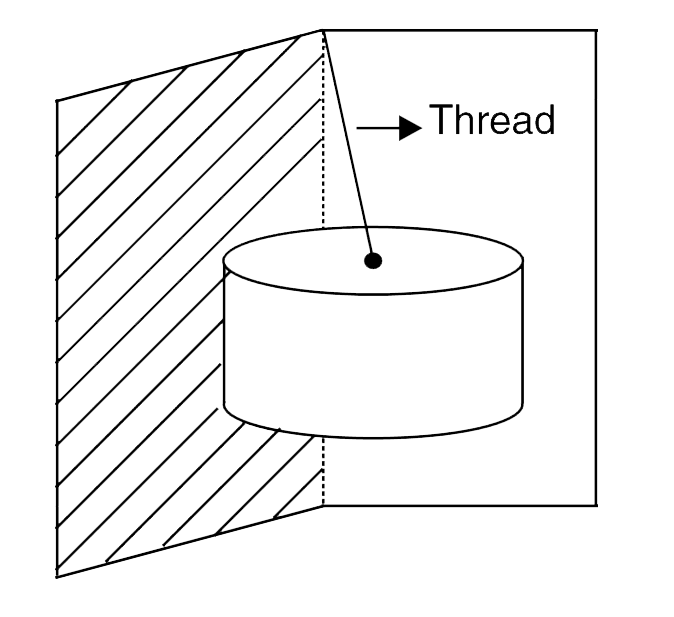 View Solution
View SolutionA horizontal uniform rod of mass 'm' has its left end hinged to the fixed incline plane, while its right end rrests on the top of a uniform cylinder of mass 'm' which in turn is at rest on the fixed inclined plane as shown. The coefficient of friction between the cylinder and rod, and between the cylinder and inclined plane, is sufficient to keep the cylinder at rest.
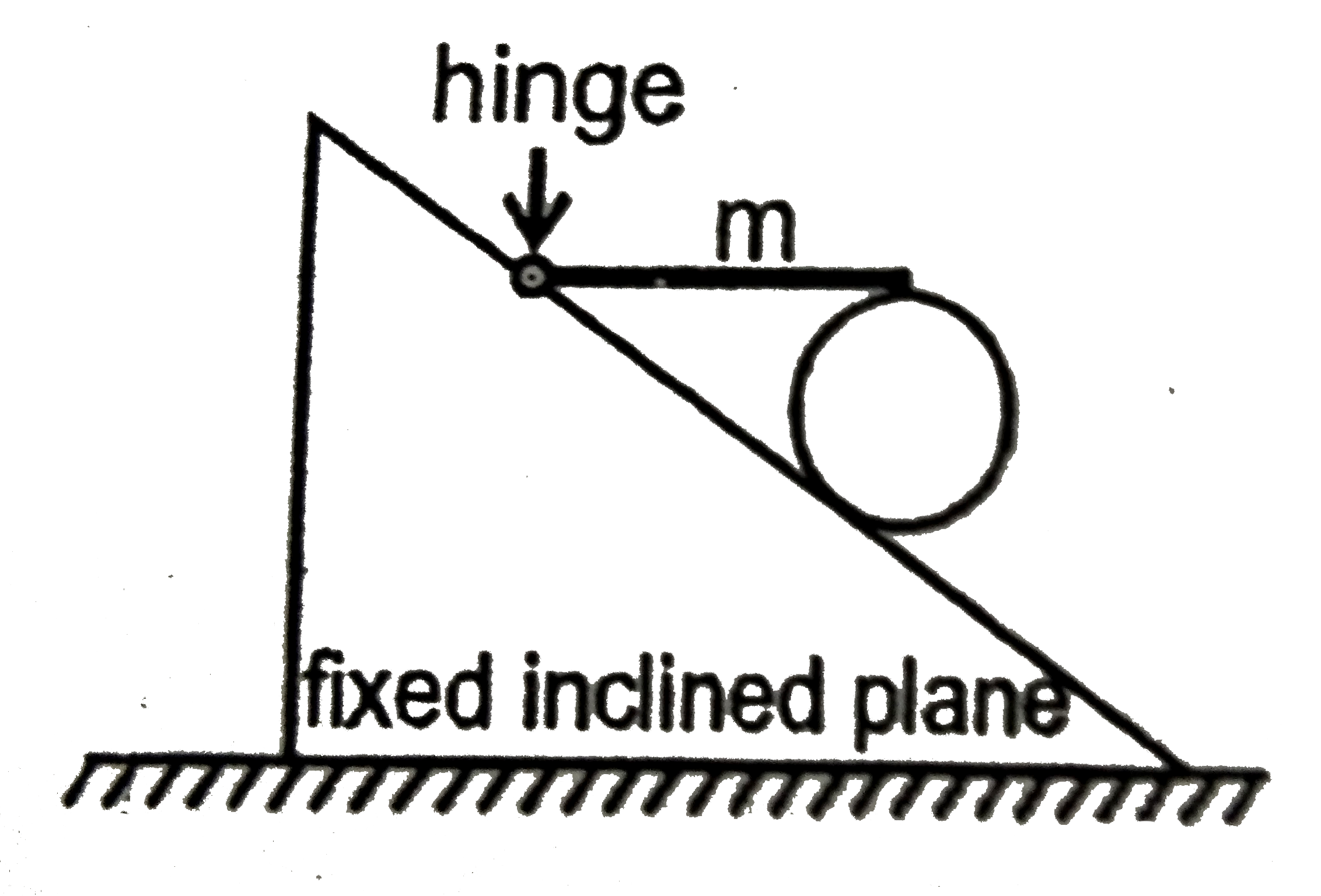
The magnitude of normal reaction exerted by the inclinded plane on the cylinder is :View SolutionA cylinder has a diameter of 20 cm. The area of the curved surface is 100 cm2. Find the volume of the cylinder (in. cm3).
View SolutionA cylinder rests on a horizontal rotating disc, as shown in the figure. Find at what angular velocity, ω, the cylinder falls off the disc, if the distance between the axes of the disc and cylinder is R, and the coefficient of friction μ>D/h where D is the diameter of the cylinder and It is its height.
 View Solution
View SolutionConsider a cylinder of mass M and radius R lying on a rough horizontal plane. It has a plank lying on its top as shown in the figure. A force F is applied on the plank such that the plank moves and causes the cylinder to roll. The plank always remains horizontal. There is no slipping at any point to contact.

(a) what are the directions of the fricition forces acting at A and B on the plank and the cylinder ?
(b) Calculate the acceleration of the cylinder.
(c) Find the value of frictional force at A & B.View SolutionA uniform solid cylinder of density 0.8g/cm3 floats in equilibrium in a combination of two non-mixing liquids A and B with its axis vertical.
The densities of the liquids A and B are 0.7g/cm3 and 1.2g/cm3, respectively. The height of liquid A is hA=1.2cm. The length of the part of the cylinder immersed in liquid B is hB=0.8cm.

(a) Find the total force exerted by liquid A on the cylinder.
(b) Find h, the length of the part of the cylinder in air.
(c) The cylinder is depressed in such a way that its top surface is just below the upper surface of liquid A and is then released. Find the acceleration of the cylinder immediately after it is released.View SolutionA uniform solid cylinder of density 0.8g/cm3 floats in equilibrium in a combination of two non-mixing liquids A and B with its axis vertical.
The densities of the liquids A and B are 0.7g/cm3 and 1.2g/cm3, respectively. The height of liquid A is hA=1.2cm. The length of the part of the cylinder immersed in liquid B is hB=0.8cm.

(a) Find the total force exerted by liquid A on the cylinder.
(b) Find h, the length of the part of the cylinder in air.
(c) The cylinder is depressed in such a way that its top surface is just below the upper surface of liquid A and is then released. Find the acceleration of the cylinder immediately after it is released.View SolutionA uniform solid cylinder of density 0.8g/cm3 floats in equilibrium in a combination of two non-mixing liquids A and B with its axis vertical.
The densities of the liquids A and B are 0.7g/cm3 and 1.2g/cm3, respectively. The height of liquid A is hA=1.2cm. The length of the part of the cylinder immersed in liquid B is hB=0.8cm.

(a) Find the total force exerted by liquid A on the cylinder.
(b) Find h, the length of the part of the cylinder in air.
(c) The cylinder is depressed in such a way that its top surface is just below the upper surface of liquid A and is then released. Find the acceleration of the cylinder immediately after it is released.View Solution

